全排列打印

全排列打印
全排列的要求：

輸入：字符串"abc"。

輸出：如下圖示，

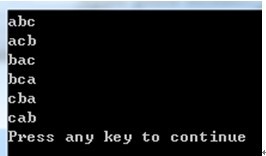
思路1——全排列的遞歸實現核心思想：

比如對於字符串”abc”，

第一步：求所有可能出現在第一個位置的字符即：a,b,c。

使用方法：把第一個字符和後面的b、c字符進行交換。

第二步：把第一個字符後面的所有字符仍然看成兩部分，即後面的第一個字符及除此之外的其他字符。然後完成後面的第一個字符與其他字符的交換。比如：第2個位置的b與第3個位置c的交換。

第三步：依次遞歸，直到末尾的’\0’為止。

全排列的遞歸實現：                                    

[cpp] 
static int g_sCnt= 0; 
  
//permutation的重載版本. 
voidpermutation(char* pStr, char* pBegin) 
{ 
       if(*pBegin == '\0') 
       { 
              ++g_sCnt; 
              cout << pStr << endl; 
       } 
       else 
       { 
              for(char* pCh = pBegin; *pCh != '\0'; ++pCh) 
              { 
                     //從第一個字符依次和後面的字符進行交換. 
                     char temp = *pCh; 
                     *pCh = *pBegin; 
                     *pBegin = temp; 
  
                     permutation(pStr,pBegin+1); 
                     
                     //交換回原樣，以便再遞歸處理後面的字符. 
                     temp = *pCh; 
                     *pCh = *pBegin; 
                     *pBegin = temp; 
  
              }//end for 
       }//end else 
} 
//全排列處理函數 
voidpermutation(char* pStr) 
{ 
    if(pStr== NULL) 
        { 
              return; 
        } 
       else 
        { 
              permutation(pStr,pStr); 
        } 
} 
  
int main() 
{ 
    char strSrc[] = "abcd"; 
    permutation(strSrc); 
    cout<< "共 " << g_sCnt << " 種排列!" <<endl; 
         
return 0; 
} 

思路2——全排列的STL實現：

有時候遞歸的效率使得我們不得不考慮除此之外的其他實現，很多把遞歸算法轉換到非遞歸形式的算法是比較難的，這個時候我們不要忘記了標准模板庫STL已經實現的那些算法，這讓我們非常輕松。

STL有一個函數next_permutation()，它的作用是如果對於一個序列，存在按照字典排序後這個排列的下一個排列，那麼就返回true且產生這個排列，否則返回false。

注意，為了產生全排列，這個序列要是有序的，也就是說要調用一次sort。

實現很簡單，我們看一下代碼：

[cpp] 
 void permutation(char* str) 
{ 
       int length = strlen(str); 
  
       //第1步：排序 
    sort(str,str+length); 
  
       //第2步：調用函數next_permutation 
    do 
    { 
        for(int i=0; i<length; i++) 
              { 
                     cout<<str[i]; 
              } 
        cout << endl; 
    }while(next_permutation(str,str+length)); 
    
} 
  
int main() 
{ 
    char str[] = "acb"; 
    permutation(str); 
    
    return 0; 
} 

思路3：全排列的字典樹實現

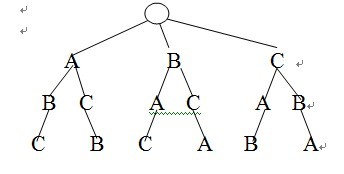
待筆者研究透字典樹後深入寫出該算法。