該題就是求一個字符串的最長回文子串,就是一個滿足本身是回文的最長的子串。
該題貌似可以用後綴數組和擴展kmp做,但是好像後綴數組貌似會tle,改學了下
一個專門的叫Manacher算法的東西。。。
該算法說起來也不是太復雜,比較容易看懂的那種,當然是接觸過其它字符串算法
的前提下了。記得以前就看了看,硬是沒看懂,想不到現在這麼快就明白了。
該算法需要額外的O(N)空間。說起來是空間換時間吧。
大概的思路是先預處理字符串,使其成為一個長度一定為偶數的串。而且第一個字符
是'$',假設'$'沒有在原串出現過。然後再在原來的每個字符前面加上'#',最後再加個
'#'。比如,abc就變成了$#a#b#c#。現在再對新的字符串進行處理。
開一個新的數組nRad[MAX],nRad[i]表示新串中第i個位置向左邊和向右邊同時擴展
並且保持對稱的最大距離。如果求出了nRad數組後,有一個結論,nRad[i]-1恰好表示原串
對應的位置能夠擴展的回文子串長度。這個的證明,應該比較簡單,因為新串基本上是原串
的2倍了,而且新串每一個有效字符兩側都有插入的#,這個找個例子看下就知道是這樣了。
最重要的是如何求出nRad數組。
求這個數組的算法也主要是利用了一些間接的結論優化了nRad[i]的初始化值。比如我們求
nRad[i]的時候,如果知道了i以前的nRad值,而且知道了前面有一個位置id,能夠最大的向
兩邊擴展距離max。那麼有一個結論,nRad[i] 能夠初始化為min(nRad[2*id - i], max - i),
然後再進行遞增。關鍵是如何證明這個,這個的證明,對照圖片就很清楚了。
證明如下:
當 mx - i > P[j] 的時候,以S[j]為中心的回文子串包含在以S[id]為中心的回文子串中,由於 i 和 j 對稱,
以S[i]為中心的回文子串必然包含在以S[id]為中心的回文子串中,所以必有 P[i] = P[j],見下圖。
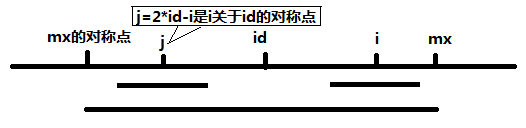
當 P[j] > mx - i 的時候,以S[j]為中心的回文子串不完全包含於以S[id]為中心的回文子串中,但是基於
對稱性可知,下圖中兩個綠框所包圍的部分是相同的,也就是說以S[i]為中心的回文子串,其向右至少會
擴張到mx的位置,也就是說 P[i] >= mx - i。至於mx之後的部分是否對稱,就只能老老實實去匹配了。
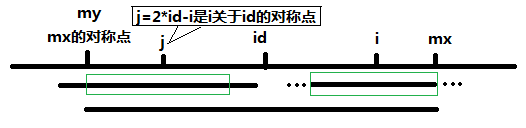
這個就說明得很清楚了。。。
代碼如下:
#include <stdio.h>
#include <string.h>
#include <algorithm>
using namespace std;
const int MAX = 110010 * 2;
char szIn[MAX];
char szOut[MAX];
int nRad[MAX];
int Proc(char* pszIn, char* pszOut)
{
int nLen = 1;
*pszOut++ = '$';
while (*pszIn)
{
*pszOut++ = '#';
nLen++;
*pszOut++ = *pszIn++;
nLen++;
}
*pszOut++ = '#';
*pszOut = '\0';
return nLen + 1;
}
void Manacher(int* pnRad, char* pszStr, int nN)
{
int nId = 0, nMax = 0;
//pnRad[0] = 1;
for (int i = 0; i < nN; ++i)
{
if (nMax > i)
{
pnRad[i] = min(pnRad[2 * nId - i], nMax - i);
}
else pnRad[i] = 1;
while (pszStr[i + pnRad[i]] == pszStr[i - pnRad[i]])
{
++pnRad[i];
}
if (pnRad[i] + i > nMax)
{
nMax = pnRad[i] + i;
nId = i;
}
}
}
int main()
{
while (scanf("%s", szIn) == 1)
{
int nLen = Proc(szIn, szOut);
Manacher(nRad, szOut, nLen);
int nAns = 1;
for (int i = 0; i < nLen; ++i)
{
nAns = max(nRad[i], nAns);
}
printf("%d\n", nAns - 1);
}
return 0;
}