題目開始以為可以用二分匹配解決,但是要和兩邊都求最大匹配,沒辦法解決。但是想到最大流可以解決二分匹配問題,那麼就建圖用網絡流解決。
但是一開始是這樣建圖源點-food-牛-drink-匯點,這樣雖然滿足每份food和drink只能給一頭牛吃,但是沒法解決每頭牛只能吃一份的問題。
難在建圖,如果是這樣,源點-food-牛-牛-drink-匯點,將牛拆成兩個點,裡面的邊權值全為1.用效率不是很高的Ek算法就能解決。EK算法比較好理解。
轉:
最近又復習了下最大流問題,每次看這部分的內容都會有新的收獲。可以說最大流問題的資料網上一搜一大把,根本沒有必要自己寫;但是大部分資料上的專業術語太多了,初學很難理解,至少我當年學這部分的時候前幾次就沒有看懂。所以我准備備份一點個人的理解。
圖-1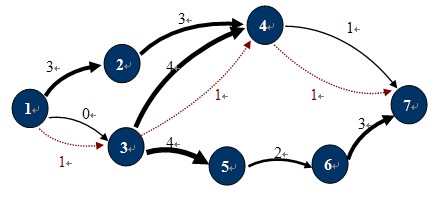
如圖-1所示,在這個運輸網絡中,源點S和匯點T分別是1,7,各邊的容量為C(u,v)。圖中紅色虛線所示就是一個可行流。標准圖示法如圖-2所示:
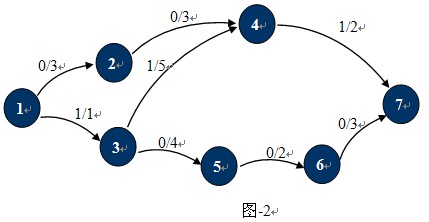
其中p(u,v) / c(u,v)分別表示該邊的實際流量與最大容量。
關於最大流
熟悉了什麼是網絡流,最大流也就很好理解了。就是對於任意的u∈V-{s},使得p(s,u)的和達到最大。上面的運輸網絡中,最大流如圖-3所示:MaxFlow=p(1,2)+p(1,3)=2+1=3。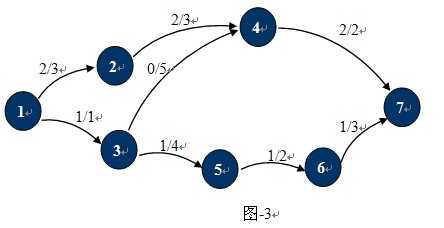
在介紹最大流問題之前,先介紹幾個概念:殘余網絡,增廣路徑,反向弧,最大流定理以及求最大流的Ford-Fulkerson方法。
殘余網絡 增廣路徑 反向弧
觀察下圖-4,這種狀態下它的殘余網絡如圖-5所示:
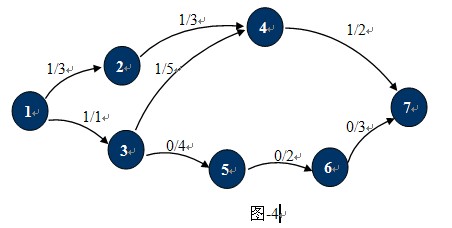
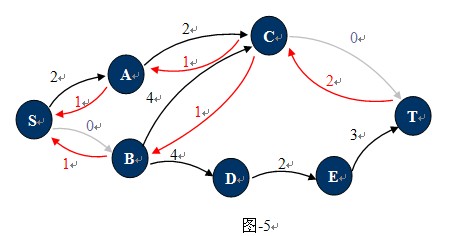
也許現在你已經知道什麼是殘余網絡了,對於已經找到一條從S 到T的路徑的網絡中,只要在這條路徑上,把C(u,v)的值更新為C(u,v)-P(u,v),並且添加反向弧C(v,u)。對應的增廣路徑Path為殘留網絡上從S到T的一條簡單路徑。圖-4中1,2,4,7就是一條增廣路徑,當然還有1,3,4,7。
此外在未做任何操作之前,原始的有向圖也是一個殘余網絡,它僅僅是未做任何更新而已。
最大流定理
如果殘留網絡上找不到增廣路徑,則當前流為最大流;反之,如果當前流不為最大流,則一定有增廣路徑。
Ford-Fulkerson方法
介紹完上面的概念之後,便可以用Ford-Fulkerson方法求最大流了。為什麼叫Ford-Fulkerson方法而不是算法,原因在於可以用多種方式實現這一方法,方式並不唯一。下面介紹一種基於廣度優先搜索(BFS)來計算增廣路徑P的算法:Edmonds-Karp算法。
算法流程如下:
設隊列Q:存儲當前未訪問的節點,隊首節點出隊後,成為已檢查的標點;
Path數組:存儲當前已訪問過的節點的增廣路徑;
Flow數組:存儲一次BFS遍歷之後流的可改進量;
Repeat:
Path清空;
源點S進入Path和Q,Path[S]=0,Flow[S]=+∞;
While Q非空 and 匯點T未訪問 do
Begin
隊首頂點u出對;
For每一條從u出發的弧(u,v) do
If v未訪問 and 弧(u,v) 的流量可改進;
Then Flow[v]=min(Flow[u],c[u][v]) and v入隊 and Path[v]=u;
End while
If(匯點T已訪問)
Then 從匯點T沿著Path構造殘余網絡;
Until 匯點T未被訪問
代碼:
[cpp]
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <math.h>
#define inf 1000
#define nMax 410
#define Max(a,b) (a>b?a:b)
#define Min(a,b) (a<b?a:b)
int map[nMax][nMax];
int N,F,D;
int path[nMax];
int queue[nMax * 100];
int head,end;
//bool flag[nMax];
//廣搜求一條增廣路
int bfs()
{
int minFlow = inf,u;
memset(path, -1, sizeof(path));
head = 0;
end = 1;
queue[head] = 0;
while (head < end)
{
u = queue[head ++];
if (u == 2 * N + F + D + 1)
{
break;
}
for (int i = 1; i <= 2 * N + F + D + 1; ++ i)
{
if (path[i] == -1 && map[u][i] )
{
if (minFlow > map[u][i])
{
minFlow = map[u][i];
}
queue[end ++] = i;
path[i] = u;
}
}
}
if (path[2 * N + F + D + 1] == -1)
{
return -1;
}
return minFlow;
}
//EK算法,每次廣搜得到一條增廣路徑,然後更新殘留網絡
void Edmods_Karp()
{
int flow, maxFlow = 0, now, pre;
while ((flow = bfs()) != -1)
{
maxFlow += flow;
now = 2 * N + F + D + 1;
while (now != 0)
{
pre = path[now];
map[pre][now] -= flow;
map[now][pre] += flow;
now = pre;
}
}
printf("%d\n", maxFlow);
}
//按照源點-食物-牛-牛-飲料-匯點的順序建圖
void buildMap()
{
int fNum,dNum,fd;
while (scanf("%d %d %d", &N, &F, &D) != EOF)
{
memset(map, 0, sizeof(map));
//memset(flag, false, sizeof(flag));
for (int i = 1; i <= N; ++ i)
{
scanf("%d %d", &fNum, &dNum);
for (int j = 0; j < fNum; ++ j)
{
scanf("%d", &fd);
map[0][fd] = 1;
map[fd][i + F] = 1;
}
map[i + F][i + F + N] = 1;
for (int j = 0; j < dNum; ++ j)
{
scanf("%d", &fd);
map[fd + 2 * N + F][F + 2 * N + D + 1] = 1;
map[i + F + N][fd + 2 * N + F] = 1;
}
}
Edmods_Karp();
}
}
//注意這裡給點編號,0-源點,1-F是食物,F+1-F+N是牛左點,F+N+1-F+N+N是牛右點,F+N+N+1-F+N+N+D是drink飲料點,F+N+N+D+1是匯點
int main()
{
buildMap();
return 0;
}