分布排序(distribution sorts)算法大串講
本文內容框架:
§1 鴿巢排序(Pigeonhole)
§2 桶排序(Bucket Sort)
§3 基數排序(Radix Sort)
§4 計數排序(Counting Sort)
§5 Proxmap Sort
§6 珠排序(Bead Sort)
§7 小結
本文介紹的排序算法是基於分配、收集的排序算法,分配排序的基本思想:排序過程無須比較關鍵字,而是通過"分配"和"收集"過程來實現排序.它們的時間復雜度可達到線性階:O(n)。不受比較排序算法時間復雜度O(nlogn)的下限限制。
§1 鴿巢排序(Pigeonhole)
鴿巢排序(Pigeonhole sort)
鴿巢排序(Pigeonhole sort),也被稱作基數分類, 是一種時間復雜度為O(n)且在不可避免遍歷每一個元素並且排序的情況下效率最好的一種排序算法。但它只有在差值(或者可被映射在差值)很小的范圍內的數值排序的情況下實用,同時也要求元素個數(n)和成為索引的值(N)大小相當。
鴿巢排序(Pigeonhole sort)算法的時間復雜度都是O(N+n),空間復雜度是O(N)。
鴿巢排序(Pigeonhole sort)算法的思想就是使用一個輔助數組,這個輔助數組的下標對應要排序數組的元素值即使用輔助數組的下標進行排序,輔助數組元素的值記錄該下標元素值的在要排序數組中的個數。
鴿巢排序(Pigeonhole sort)算法步驟:
1.對於給定的一組要排序的數組,需要初始化一個空的輔助數組(“鴿巢”),把初始數組中的每個值作為一個key(“鴿巢”)即輔助數組的索引即是待排序數組的值。
2.遍歷初始數組,根據每個值放入輔助數組對應的“鴿巢”
3.順序遍歷輔助數組,把輔助數組“鴿巢”中不為空的數放回初始數組中
鴿巢排序(Pigeonhole sort)算法實現舉例
C代碼
void PigeonholeSort(int *array, int length)
{
int b[256] = {0};
int i,k,j = 0;
for(i=0; i<length; i++)
b[array[i]]++;
for(i=0; i<256; i++)
for(k=0; k<b[i]; k++)
array[j++] = i;
}
其實作者覺得鴿巢排序(Pigeonhole sort)的原理跟哈希表的原理類似——根據關鍵字的key就可以得到關鍵字的存儲位置。
§2 桶排序(Bucket Sort)
箱排序(Bin Sort)
桶排序 (Bucket sort)或所謂的箱排序,是一個排序算法,工作的原理是將陣列分到有限數量的桶子裡。每個桶子再個別排序(有可能再使用別的排序算法或是以遞回方式繼續使用桶排序進行排序)。桶排序是鴿巢排序的一種歸納結果。當要被排序的陣列內的數值是均勻分配的時候,桶排序使用線性時間(Θ(n))。但桶排序並不是比較排序,不受到 O(n log n) 下限的影響。
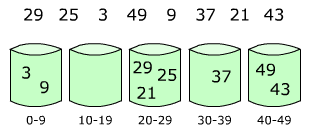
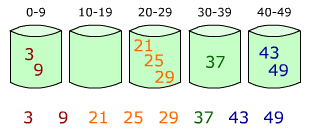
1、箱排序的基本思想
箱排序也稱桶排序(Bucket Sort),其基本思想是:設置若干個箱子,依次掃描待排序的記錄R[0],R[1],…,R[n-1],把關鍵字等於k的記錄全都裝入到第k個箱子裡(分配),然後按序號依次將各非空的箱子首尾連接起來(收集)。
【例】要將一副混洗的52張撲克牌按點數A<2<…<J<Q<K排序,需設置13個"箱子",排序時依次將每張牌按點數放入相應的箱子裡,然後依次將這些箱子首尾相接,就得到了按點數遞增序排列的一副牌。
2、箱排序中,箱子的個數取決於關鍵字的取值范圍。
若R[0..n-1]中關鍵字的取值范圍是0到m-1的整數,則必須設置m個箱子。因此箱排序要求關鍵字的類型是有限類型,否則可能要無限個箱子。
3、箱子的類型應設計成鏈表為宜
一般情況下每個箱子中存放多少個關鍵字相同的記錄是無法預料的,故箱子的類型應設計成鏈表為宜。
4、為保證排序是穩定的,分配過程中裝箱及收集過程中的連接必須按先進先出原則進行。
(1) 實現方法一
每個箱子設為一個鏈隊列。當一記錄裝入某箱子時,應做人隊操作將其插入該箱子尾部;而收集過程則是對箱子做出隊操作,依次將出隊的記錄放到輸出序列中。
(2) 實現方法二
若輸入的待排序記錄是以鏈表形式給出時,出隊操作可簡化為是將整個箱子鏈表鏈接到輸出鏈表的尾部。這只需要修改輸出鏈表的尾結點中的指針域,令其指向箱子鏈表的頭,然後修改輸出鏈表的尾指針,令其指向箱子鏈表的尾即可。
桶排序算法實現舉例
Cpp代碼
#include <iostream>
#include <list>
using namespace std;
struct Node
{
double value;
Node *next;
};
//桶排序主程序
void bucketSort(double* arr, int length)
{
Node key[10];
int number = 0;
Node *p, *q;//插入節點臨時變量
int counter = 0;
for(int i = 0; i < 10; i++)
{
key[i].value = 0;
key[i].next = NULL;
}
for(int i = 0; i < length; i++)
{
Node *insert = new Node();
insert->value = arr[i];
insert->next = NULL;
number = arr[i] * 10;
if(key[number].next == NULL)
{
key[number].next = insert;
}
else
{
p = &key[number];
q = key[number].next;
while((q != NULL) && (q->value <= arr[i]))
{
q = q->next;
p = p->next;
}
insert->next = q;
p->next = insert;
}
}
for(int i = 0; i < 10; i++)
{
p = key[i].next;
if(p == NULL)
continue;
while(p != NULL)
{
arr[counter++] = p->value;
p = p->next;
}
}
}
int main()
{
double a[] = {0.78, 0.17, 0.39, 0.26, 0.72, 0.94, 0.21, 0.12, 0.23, 0.68};
bucketSort(a, 10);
for(int i = 0; i < 10; i++)
{
cout << a[i] << " ";
}
cout << endl;
return 0;
}
5、算法簡析
分配過程的時間是O(n);收集過程的時間為O(m) (采用鏈表來存儲輸入的待排序記錄)或O(m+n)。因此,箱排序的時間為O(m+n)。若箱子個數m的數量級為O(n),則箱排序的時間是線性的,即O(n),但最壞情況仍有可能是 O(n ^ 2)。
桶排序只適用於關鍵字取值范圍較小的情況,否則所需箱子的數目 m 太多導致浪費存儲空間和計算時間。
桶排序能夠擴展為對整數元組序列進行排序,此時按照字典序排序。在面試的海量數據處理題目中,桶排序也很有作用。如對每天數以億計的數據進行排序,直接排序即使采用nlgn的算法,依然是一件很恐怖的事情,內存也無法容納如此多的數據。這時桶排序就可以有效地降低數據的數量級,再對降低了數量級的數據進行排序,可以得到比較良好的效果。
§3 基數排序(Radix Sort)
基數排序(Radix Sort)
基數排序(Radix Sort)是對桶排序的改進和推廣。唯一的區別是基數排序強調多關鍵字,而桶排序沒有這個概念,換句話說基數排序對每一種關鍵字都進行桶排序,而桶排序同一個桶內排序可以任意或直接排好序。
1、單關鍵字和多關鍵字
文件中任一記錄R[i]的關鍵字均由d個分量
構成。
若這d個分量中每個分量都是一個獨立的關鍵字,則文件是多關鍵字的(如撲克牌有兩個關鍵字:點數和花色);否則文件是單關鍵字的,
(0≤j<d)只不過是關鍵字中其中的一位(如字符串、十進制整數等)。
多關鍵字中的每個關鍵字的取值范圍一般不同。如撲克牌的花色取值只有4種,而點數則有13種。單關鍵字中的每位一般取值范圍相同。
2、基數
設單關鍵字的每個分量的取值范圍均是:
C0≤kj≤Crd-1(0≤j<d)
可能的取值個數rd稱為基數。
基數的選擇和關鍵字的分解因關鍵宇的類型而異:
(1) 若關鍵字是十進制整數,則按個、十等位進行分解,基數rd=10,C0=0,C9=9,d為最長整數的位數;
(2) 若關鍵字是小寫的英文字符串,則rd=26,Co='a',C25='z',d為字符串的最大長度。
3、基數排序的基本思想
基數排序的基本思想是:從低位到高位依次對Kj(j=d-1,d-2,…,0)進行箱排序。在d趟箱排序中,所需的箱子數就是基數rd,這就是"基數排序"名稱的由來。
基數排序的時間復雜度是 O(k·n),其中n是排序元素個數,k是數字位數。注意這不是說這個時間復雜度一定優於O(n·log(n)),因為k的大小一般會受到 n 的影響。基數排序所需的輔助存儲空間為O(n+rd)。
基數排序的方式可以采用LSD(Least significant digital)或MSD(Most significant digital),LSD的排序方式由鍵值的最右邊開始,而MSD則相反,由鍵值的最左邊開始。
基數排序算法實現舉例
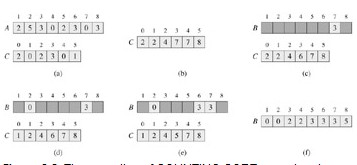
C代碼
#include <stdio.h>
#include <stdlib.h>
void radixSort(int[]);
int main(void) {
int data[10] = {73, 22, 93, 43, 55, 14, 28, 65, 39, 81};
printf("\n排序前: ");
int i;
for(i = 0; i < 10; i++)
printf("%d ", data[i]);
putchar('\n');
radixSort(data);
printf("\n排序後: ");
for(i = 0; i < 10; i++)
printf("%d ", data[i]);
return 0;
}
void radixSort(int data[]) {
int temp[10][10] = {0};
int order[10] = {0};
int n = 1;
while(n <= 10) {
int i;
for(i = 0; i < 10; i++) {
int lsd = ((data[i] / n) % 10);
temp[lsd][order[lsd]] = data[i];
order[lsd]++;
}
// 重新排列
int k = 0;
for(i = 0; i < 10; i++) {
if(order[i] != 0) {
int j;
for(j = 0; j < order[i]; j++, k++) {
data[k] = temp[i][j];
}
}
order[i] = 0;
}
n *= 10;
}
}
基數排序應用到字符串處理的倍增算法裡面,這個倍增算法,要反復的進行排序。如果排序能快一點,這個程序就能快很多。
§4 計數排序(Counting Sort)
計數排序(Counting sort)
計數排序(Counting sort)是一種穩定的排序算法,和基數排序一樣都是桶排序的變體。計數排序使用一個額外的數組C,其中第i個元素是待排序數組A中值小於等於i的元素的個數。然後根據數組C來將A中的元素排到正確的位置。
計數排序的原理
設被排序的數組為A,排序後存儲到B,C為臨時數組。所謂計數,首先是通過一個數組C[i]計算大小等於i的元素個數,此過程只需要一次循環遍歷就可以;在此基礎上,計算小於或者等於i的元素個數,也是一重循環就完成。下一步是關鍵:逆序循環,從length[A]到1,將A[i]放到B中第C[A[i]]個位置上。原理是:C[A[i]]表示小於等於a[i]的元素個數,正好是A[i]排序後應該在的位置。而且從length[A]到1逆序循環,可以保證相同元素間的相對順序不變,這也是計數排序穩定性的體現。在數組A有附件屬性的時候,穩定性是非常重要的。
計數排序的前提及適用范圍
A中的元素不能大於k,而且元素要作為數組的下標,所以元素應該為非負整數。而且如果A中有很大的元素,不能夠分配足夠大的空間。所以計數排序有很大局限性,其主要適用於元素個數多,但是普遍不太大而且總小於k的情況,這種情況下使用計數排序可以獲得很高的效率。由於用來計數的數組C的長度取決於待排序數組中數據的范圍(等於待排序數組的最大值與最小值的差加上 1),這使得計數排序對於數據范圍很大的數組,需要大量時間和內存。例如:計數排序是用來排序0到100之間的數字的最好的算法,但是它不適合按字母順序排序人名。但是,計數排序可以用在基數排序中的算法來排序數據范圍很大的數組。
當輸入的元素是 n 個 0 到 k 之間的整數時,它的運行時間是 Θ(n + k)。計數排序不是比較排序,排序的速度快於任何比較排序算法。
計數排序算法的步驟:
1.找出待排序的數組中最大和最小的元素
2.統計數組中每個值為i的元素出現的次數,存入數組C的第i項
3.對所有的計數累加(從C中的第一個元素開始,每一項和前一項相加)
4.反向填充目標數組:將每個元素i放在新數組的第C(i)項,每放一個元素就將C(i)減去1
計數排序算法實現舉例
C代碼
#include <stdio.h>
#include <conio.h>
#define MAX 1000
//函數原型
void counting_sort(int A[],int length_A,int B[],int k);
//測試代碼
int main()
{
int A[]={-1,2,6,5,4,8,9,7,1,10,3};//1到10,十個測試數據
int B[11]={0};
int k=10;//所有測試數據都處於0到k之間
counting_sort(A,10,B,k);
for(int i=1;i<11;i++)
printf("%d ",B[i]);
getch();
}
//計數排序
void counting_sort(int A[],int length_A,int B[],int k)
{
int C[MAX]={0};//C是臨時數組
for(int i=1;i<=length_A;i++)
C[A[i]]++;
//此時C[i]包含等於i的元素個數
for(int i=1;i<=k;i++)
C[i]=C[i]+C[i-1];
//此時C[i]包含小於或者等於i的元素個數
for(int i=length_A;i>=1;i--)//從length_A到1逆序遍歷是為了保證相同元素排序後的相對順序不改變
{ //如果從1到length_A,則相同元素的相對順序會逆序,但結果也是正確的
B[C[A[i]]]=A[i];
C[A[i]]--;
}
}
可以使用鏈表節省輔助數組C的空間,只存儲出現的出現元素情況。
§5 Proxmap Sort
Proxmap Sort
Proxmap Sort是桶排序和基數排序的改進。ProxMap的排序采用不同的方法來排序,這在概念上是類似哈希。該算法使用桶技術對哈希方法進行改變,桶的大小不相同。
Technique:
Create 4 arrays and initialize
int HitList[ARRAYSIZE] -- Keeps a count of the number of hits at each index in the sorted array. HitList[x] holds a count of the number of items whose keys hashed to x. Initialize to all 0.
int Location[ARRAYSIZE] -- Indices in the sorted array calculated using the hash function. Item x in the unsorted array has its hash index stored in Location[x]. Does not need to be initialized.
int ProxMap[ARRAYSIZE] -- Starting index in the sorted array for each bucket. If HitList[x] is not 0 then ProxMap[x] contains the starting index for the bucket of keys hashing to x. Initialize to all keys to -1 (unused).
StructType DataArray2[ARRAYSIZE] -- Array to hold the sorted array. Initialize to all -1 (unused).
Use the keys of the unsorted array and a carefully chosen hash function to generate the indices into the sorted array and save these. The hash function must compute indices always in ascending order. Store each hash index in the Location[] array. Location[i] will hold the calculated hash index for the ith structure in the unsorted array.
HIdx = Hash(DataArray[i]);
Location[i] = HIdx;
Care must be taken in selecting the hash function so that the keys are mapped to the entire range of indexes in the array. A good approach is to convert the keys to integer values if they are strings, then map all keys to floats in the range 0<= Key < 1. Finally, map these floats to the array indices using the following formulas:
/* Map all integer keys to floats in range 0<= Key < 1 */
KeyFloat = KeyInt / (1 + MAXKEYINTVALUE);
/* Map all float keys to indices in range 0<= Index < ARRAYSIZE */
Index = floor(ARRAYSIZE * KeyFloat);
This will then produce indices insuring that all the keys are kept in ascending order (hashs computed using a mod operator will not.)
Keep a count of the number of hits at each hash index. HitList[Hidx]++
Create the ProxMap (short for proximity map) from the hit list giving the starting index in the sorted array for each bucket.
RunningTotal = 0; /* Init counter */
for(i=0; i 0) /* There were hits at this address */
{
ProxMap[i] = RunningTotal; /* Set start index for this set */
RunningTotal += HitList[i];
}
}
Move keys from the unsorted array to the sorted array using an insertion sort technique for each bucket.
In this diagram 5 sets of structures are sorted when delta = 5
Analysis: ProxMap sorting runs in a surprisingly fast O(n) time.
C代碼
/******************************************************/
/* ProxmapSort.c */
/* */
/* Proxmap sort demonstration. */
/* Author: Rick Coleman */
/* Date: April 1998 */
/******************************************************/
#include <stdio.h>
#include <conio.h>
#include "sort.h"
#include <math.h>
#define ARRAYSIZE 32
/* Prototype sort function */
void ProxmapSort(StructType DataArray[], StructType DataArray2[],int count);
int Hash(int key, int KeyMax, int KeyMin, int count);
void ProxMapInsertionSort(StructType DataArray[], StructType *theStruct,
int startIdx, int listLen);
int main(void)
{
StructType DataArray[32], DataArray2[32];
int count;
count = ReadRecords(DataArray, 32);
printf("Unsorted list of records.\n\n");
PrintList(DataArray, count);
ProxmapSort(DataArray, DataArray2, count);
printf("Sorted list of records.\n\n");
PrintList(DataArray2, count);
printf("Sorting done...\n");
getch();
return(0);
}
/***************************************/
/* ProxmapSort() */
/* */
/* Sort records on integer key using */
/* a proxmap sort. */
/***************************************/
void ProxmapSort(StructType DataArray[], StructType DataArray2[],int count)
{
int i;
int HitList[ARRAYSIZE];
int Hidx; /* Hashed index */
int ProxMap[ARRAYSIZE];
int RunningTotal; /* Number of hits */
int Location[ARRAYSIZE];
int KeyMax, KeyMin; /* Used in Hash() */
/* Initialize hit list and proxmap */
for(i=0; i<count; i++)
{
HitList[i] = 0; /* Init to all 0 hits */
ProxMap[i] = -1; /* Init to all unused */
DataArray2[i].key = -1; /* Init to all empty */
}
/* Find the largest key for use in computing the hash */
KeyMax = 0; /* Guaranteed to be less than the smallest key */
KeyMin = 32767; /* Guaranteed to be more than the largest key */
for(i=0; i<count; i++)
{
if(DataArray[i].key > KeyMax) KeyMax = DataArray[i].key;
if(DataArray[i].key < KeyMin) KeyMin = DataArray[i].key;
}
/* Compute the hit count list (note this is not a collision count, but
a collision count+1 */
for(i=0; i<count; i++)
{
Hidx = Hash(DataArray[i].key, KeyMax, KeyMin, count); /* Calculate hash index */
Location[i] = Hidx; /* Save this for later. (Step 1) */
HitList[Hidx]++; /* Update the hit count (Step 2) */
}
/* Create the proxmap from the hit list. (Step 3) */
RunningTotal = 0; /* Init counter */
for(i=0; i<count; i++)
{
if(HitList[i] > 0) /* There were hits at this address */
{
ProxMap[i] = RunningTotal; /* Set start index for this set */
RunningTotal += HitList[i];
}
}
// NOTE: UNCOMMENT THE FOLLOWING SECTION TO SEE WHAT IS IN THE ARRAYS, BUT
// COMMENT IT OUT WHEN DOING A TEST RUN AS PRINTING IS VERY SLOW AND
// WILL RESULT IN AN INACCURATE TIME FOR PROXMAP SORT.
/* ----------------------------------------------------
// Print HitList[] to see what it looks like
printf("HitList:\n");
for(i=0; i<count; i++)
printf("%d ", HitList[i]);
printf("\n\n");
getch();
// Print ProxMap[] to see what it looks like
printf("ProxMap:\n");
for(i=0; i<count; i++)
printf("%d ", ProxMap[i]);
printf("\n\n");
getch();
// Print Location[] to see what it looks like
printf("Location:\n");
for(i=0; i<count; i++)
printf("%d ", Location[i]);
printf("\n\n");
getch();
--------------------------------------------- */
/* Move the keys from A1 to A2 */
/* Assumes A2 has been initialized to all empty slots (key = -1)*/
for(i=0; i<count; i++)
{
if((DataArray2[ProxMap[Location[i]]].key == -1)) /* If the location in A2 is empty...*/
{
/* Move the structure into the sorted array */
DataArray2[ProxMap[Location[i]]] = DataArray[i];
}
else /* Insert the structure using an insertion sort */
{
ProxMapInsertionSort(DataArray2, &DataArray[i], ProxMap[Location[i]], HitList[Location[i]]);
}
}
}
/***************************************/
/* Hash() */
/* */
/* Calculate a hash index. */
/***************************************/
int Hash(int key, int KeyMax, int KeyMin, int count)
{
float keyFloat;
/* Map integer key to float in the range 0 <= key < 1 */
keyFloat = (float)(key - KeyMin) / (float)(1 + KeyMax - KeyMin);
/* Map float key to indices in range 0 <= index < count */
return((int)floor(count * keyFloat));
}
/***************************************/
/* ProxMapInsertionSort() */
/* */
/* Use insertion sort to insert a */
/* struct into a subarray. */
/***************************************/
void ProxMapInsertionSort(StructType DataArray[], StructType *theStruct,
int startIdx, int listLen)
{
/* Args: DataArray - Partly sorted array
*theStruct - Structure to insert
startIdx - Index of start of subarray
listLen - Number of items in the subarray */
int i;
/* Find the end of the subarray */
i = startIdx + listLen - 1;
while(DataArray[i-1].key == -1) i--;
/* Find the location to insert the key */
while((DataArray[i-1].key > theStruct->key) && (i > startIdx))
{
DataArray[i] = DataArray[i-1];
i--;
}
/* Insert the key */
DataArray[i] = *theStruct;
}
§6 珠排序(Bead Sort)
珠排序(Bead Sort)
珠排序是一種自然排序算法,由Joshua J. Arulanandham, Cristian S. Calude 和 Michael J. Dinneen 在2002年發展而來,並且在歐洲理論計算機協會(European Association for Theoretical Computer Science,簡稱EATCS)的新聞簡報上發表了該算法。無論是電子還是實物(digital and analog hardware)上的實現,珠排序都能在O(n)時間內完成;然而,該算法在電子上的實現明顯比實物要慢很多,並且只能用於對正整數序列進行排序。並且,即使在最好的情況,該算法也需要O(n^2) 的空間。