Dijkstra算法詳解:
在解決單源點最短路徑的問題時,常常用到經典的Dijkstra算法,其算法的本質思想是: 按路徑長度遞增依次產生最短路徑。
下面給出算法的大致流程:
1.初始化所有結點並將起始點設為標記,進入以下循環
2.在到達某點的最短路徑中找最小且未標記的點(可以用一維數組表示)
如:
數組下標:0 1 2 3 4 5
Len :- 0 5 10 2 -
這個數組表示 1號節點為初始節點,1號節點到達2號節點的最短路徑為5,到3號為10,無法到達5號(具體可以以較大的數表示其路徑)。
從中找到一個未標記且Len最短的一個,未標記用另一數組記錄
如:
數組下標:0 1 2 3 4 5
標記 :0 1 0 0 1 0
此數組表示從初始節點到達4號節點的最短路徑已找到
從以上兩個數組中可以得出:此次循環找到的點為2號節點,進入下一步
3.標記找到的點,以此標記點為中間點重新計算所有未標記點的最短路徑(更新最短路徑表)
4.循環1.2步至n-1次(n為頂點數,若最後還有未被標記的,說明無法到達此點)
下面是核心代碼:
[cpp]
while(count<n)
{
tempmin=INFINITE;
for(i=1;i<=n;i++)
{
if(in[i]==0&&Len[i]<tempmin) //find the smallest one
{
tempmin=Len[i];
si=i;
}
}
in[si]=1;
count++;
for(i=1;i<=n;i++) //updata the length
{
if(in[i]==0&&(tempmin+mGraph.matrix[si][i])<Len[i])
{
Len[i]=tempmin+mGraph.matrix[si][i];
}
}
}
核心部分是上面的兩個for循環,第一個for循環遍歷所有結點,找到未標記並且長度最短的路徑;第二個for循環也是遍歷所有結點以上面找到的最短路徑結點為中間點更新最短路徑表;注意在第一個for循環之後要標記找到的點(說明到達此點的最短路徑已找到)
下面用一個實例來具體說明:
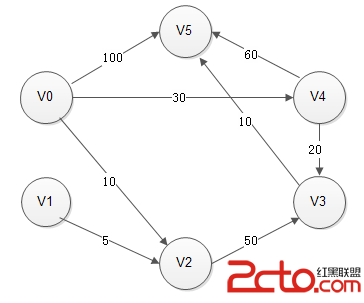
若有這樣一張有向圖(此圖為《數據結構》嚴蔚敏 p188頁,書中沒有詳細講解,現以此為實例)
V0-V5 共6個節點,節點間路徑已標出,現要求從V0到其余各節點的最短路徑;
有上面的算法流程可知,在使用Dijkstra算法時需要幾個結構來保存我們想要的信息:
1.保存這張圖的結構體
2.記錄V0到其余各節點最短路徑的數組(這裡設為Len[n+1])
3.記錄某節點是否已找到最短路徑的數組(這裡設為in[n+1])
接下來就是算法實現部分:
1.標記V0 -- in[1]=1 初始化 Len[]={INFINITE , 0 , INFINITE , 10, INFINITE , 30 , 100} 這裡數組首元素未用到,數組下標從1開始表示V0以此類推
2.第一次循環與V0相鄰的有V2、V4、V5,其中V2距離最短為10,標記V2,並且以V2為中間點(路徑為V0->V2->Vx)更新最短路表,此時V3被更新為10+50=60,。
3.進入第二次循環,此時未被標記的有V1、V3、V4、V5,,其中從V0到這些的臨時最短路分別為INFINITE、60、30、100,從中找到最小的即V4,將V4標記為1,以V4為中間點(路徑為V0->V4->Vx)更新最短路表,此時V3被更新為50,V5被更新為90。
4.進入第三次循環,此時未被標記的有V1、V3、V5,其中臨時最短路分別為INFINITE、50、90,從中找到最小的即V3,將V3標記為1,以V3為中間點(路徑為V0->V4->V3->Vx)更新最短路表,此時V5被更新成60。
5.進入第四次循環,此時未被標記的有V1、V5,其中臨時最短路分別為INFINITE、60,找到V5,標記為1,以V5為中間點更新最短路表,此時沒有元素被更新
6.進入第五次循環,這次循環沒找到任何東西
7.退出循環,Len表中即為V0到其余各個節點的最短路徑。
以上就是Dijkstra算法最基本的思想,當然,在找最短路時我們常常會需要求出到達某點的最短路徑,那麼下面,我們就來看看要怎樣記錄下到達某點的最短路徑:
在Dijkstra算法的前提下加入查詢最短路徑其實很簡單,只要在每次更新最短路時保存在該頂點的父節點序號即可,最後輸出時回退中間節點然後用堆棧輸出即可
最後直接給出完整代碼(寫的很一般,還望指教):
[cpp]
#include <stdio.h>
#include <string.h>
#define MAX_LEN 100
#define INFINITE 1000
typedef struct graph
{
int nodenum;
int edgenum;
int matrix[MAX_LEN][MAX_LEN];
}Graph;
typedef struct stack
{
int bottom;
int top;
int printout[MAX_LEN];
}mstack;
int in[MAX_LEN];
int Len[MAX_LEN];
int path[MAX_LEN];
void InitStack(mstack *s)
{
s->bottom=0;
s->top=0;
memset(s->printout,0,sizeof(int)*MAX_LEN);
}
void push(mstack *s,int m)
{
s->printout[s->top++]=m;
}
int pop(mstack *s)
{
return s->printout[--s->top];
}
void InitGraph(Graph *g,int n)
{
int i,j;
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
{ www.2cto.com
if(i==j)g->matrix[i][j]=0;
else g->matrix[i][j]=INFINITE;
}
for(i=1;i<=n;i++)
{
in[i]=0;
Len[i]=INFINITE;
path[i]=0;
}
}
int main()
{
int n,m,i,A,B,templen,count,min,tempmin,si,temp;
while(scanf("%d %d",&n,&m))
{
count=0;
Graph mGraph;
mGraph.edgenum=m;
mGraph.nodenum=n;
InitGraph(&mGraph,n);
for(i=0;i<m;i++)
{
scanf("%d %d %d",&A,&B,&templen);
mGraph.matrix[A][B]=templen;
}
in[1]=1;
path[1]=1; //sava path
Len[1]=0;
for(i=2;i<=n;i++)
{
Len[i]=mGraph.matrix[1][i]; //Init the len
if(Len[i]!=INFINITE)path[i]=1;
}
min=0;
si=1;
while(count<n-1)
{
tempmin=INFINITE;
for(i=1;i<=n;i++)
{
if(in[i]==0&&Len[i]<tempmin) //find the smallest one
{
tempmin=Len[i];
si=i;
}
}
in[si]=1;
for(i=1;i<=n;i++) //updata the length
{
if(in[i]==0&&(tempmin+mGraph.matrix[si][i])<Len[i])
{
Len[i]=tempmin+mGraph.matrix[si][i];
path[i]=si;
}
}
count++;
}
mstack s;
for(i=1;i<=n;i++)
{
temp=i;
InitStack(&s);
if(path[temp]==0)
{
printf("no path\n");
continue;
}
while(path[temp]!=1)
{
push(&s,path[temp]);
temp=path[temp];
}
printf("1-->");
while(s.bottom!=s.top)
{
printf("%d-->",pop(&s));
}
printf("%d min length is %d\n",i,Len[i]);
}
}
return 0;
}
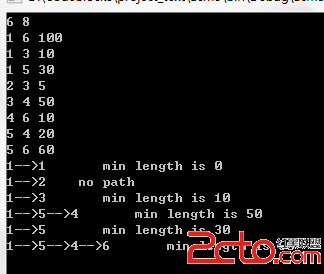
附上上面那張圖的結果(V0節點為1,V1節點為2.。。。以此類推)