改革春風吹滿地
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 11969 Accepted Submission(s): 6039
Problem Description
“ 改革春風吹滿地,
不會AC沒關系;
實在不行回老家,
還有一畝三分地。
謝謝!(樂隊奏樂)”
話說部分學生心態極好,每天就知道游戲,這次考試如此簡單的題目,也是雲裡霧裡,而且,還竟然來這麼幾句打油詩。 www.2cto.com
好呀,老師的責任就是幫你解決問題,既然想種田,那就分你一塊。
這塊田位於浙江省溫州市蒼南縣靈溪鎮林家鋪子村,多邊形形狀的一塊地,原本是linle 的,現在就准備送給你了。不過,任何事情都沒有那麼簡單,你必須首先告訴我這塊地到底有多少面積,如果回答正確才能真正得到這塊地。
發愁了吧?就是要讓你知道,種地也是需要AC知識的!以後還是好好練吧...
Input
輸入數據包含多個測試實例,每個測試實例占一行,每行的開始是一個整數n(3<=n<=100),它表示多邊形的邊數(當然也是頂點數),然後是按照逆時針順序給出的n個頂點的坐標(x1, y1, x2, y2... xn, yn),為了簡化問題,這裡的所有坐標都用整數表示。
輸入數據中所有的整數都在32位整數范圍內,n=0表示數據的結束,不做處理。
Output
對於每個測試實例,請輸出對應的多邊形面積,結果精確到小數點後一位小數。
每個實例的輸出占一行。
Sample Input
3 0 0 1 0 0 1
4 1 0 0 1 -1 0 0 -1
0
Sample Output
0.5
2.0
補充點知識點,這道題就不難了
已知三角形三頂點坐標,求三角形面積的表達式已知直角坐標系3點p(a,b),m(c,d),n(e,f) 求三角形pmn面積的表達式!
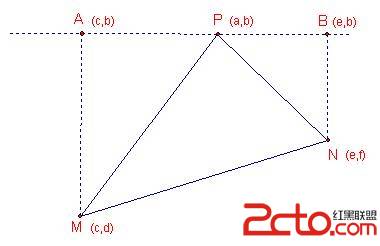
解:
無論三角形的頂點位置如何,△PMN總可以用一個直角梯形(或矩形)和兩個直角三角形面積的和差來表示
而在直角坐標系中,已知直角梯形和直角三角形的頂點的坐標,其面積是比較好求的。
下面以一種情形來說明這個方法,其它情形方法一樣,表達式也一樣(表達式最好加上絕對值,確保是正值)
如圖情形(P在上方,M在左下,N在右下),過P作X軸的平行線L,作MA⊥L,NB⊥L(設P在A、B之間)
則A、B的坐標是A(c,b),B(e,b)
所以PA=a-c,PB=e-a,AM=b-d,BN=b-f,AB=e-c
所以S△PMN=S梯形AMNB-S△PAM-S△PBN
=(b-d+b-f)(e-c)/2-(b-d)(a-c)/2-(b-f)(e-a)/2
=(ad+be+cf-af-bc-de)/2
代碼一次性AC:
[cpp]
#include<iostream>
#include<iomanip>
using namespace std;
struct node{
int x;
int y;
};
int main(){
int n,i;
node a[100];
while(cin>>n && n){
for(i=0;i<n;i++){
cin>>a[i].x>>a[i].y;
}
double sum=0;
for(i=1;i<n-1;i++){
sum+=(a[0].x*a[i+1].y + a[0].y*a[i].x + a[i+1].x*a[i].y - a[0].x*a[i].y -a[0].y*a[i+1].x -a[i+1].y*a[i].x)/2.0;
}
cout<<fixed<<setprecision(1)<<-sum<<endl;
}
return 0;
}
#include<iostream>
#include<iomanip>
using namespace std;
struct node{
int x;
int y;
};
int main(){
int n,i;
node a[100];
while(cin>>n && n){
for(i=0;i<n;i++){
cin>>a[i].x>>a[i].y;
}
double sum=0;
for(i=1;i<n-1;i++){
sum+=(a[0].x*a[i+1].y + a[0].y*a[i].x + a[i+1].x*a[i].y - a[0].x*a[i].y -a[0].y*a[i+1].x -a[i+1].y*a[i].x)/2.0;
}
cout<<fixed<<setprecision(1)<<-sum<<endl;
}
return 0;
}