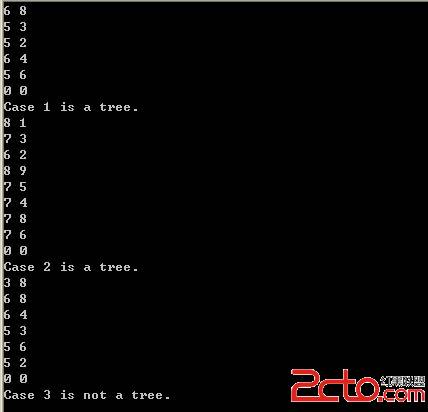
【問題描述】
樹是一種大家都不陌生的數據結構,它有可能是一顆空樹或是一些滿足要求的節點連接而成的有向邊的集合。
一棵樹只有一個根節點,根節點沒有指向它的邊。
除了根節點的每一個節點都只有一條邊指向它。
出現環的圖都不是樹。
對一些節點連接而成的有向邊的集合進行判定,判定每一組的輸入數據構成的圖是否是一棵樹。
【輸入】
每輸入一對都為0的數時,表示一組數據輸入完畢。每條邊由一對正整數表示,第一個數為有向邊的起始點,第二個數為有向邊的終止點。一對負數的輸入表示輸入的結束。
【輸出】
每組測試數據輸出一行判定結果,若輸入的圖為樹,則輸出“Case k is a tree.”,否則輸出“Case k is not a tree.”。其中k表示每組數據的編號(編號從1開始)。
【解題報告】
運用並查集可以判定一個圖是否為樹。
根據樹的定義與特點,需考慮的情況有:
(1)樹中節點至多只能有一個父節點;
(2)樹中不能出現環;
(3)構成的圖只能有一個根節點,否則構成的將是森林而不是一棵樹。
通過觀察輸入輸出可知,題中編號是隨即的,所以在編程中要對出現的點標記才能判斷。
Step1:對每對輸入的根節點標記表示這些節點出現過,進行並操作。並操作時兩個節點不能有相同的根節點否則將構成環;假設b節點要接到a上,則要保證b節點是一個根節點,否則若進行並操作,b將會有兩個父節點;若無以上情況,則可以合並兩棵樹。 .www.2cto.com
Step 2:每組數據輸入結束後,要計算整個圖中的根節點總數,若根節點總數不為1,則構成的圖不是一棵樹。
Step 3:根據以上判斷就可以輸出結果了,每組結果輸出後要初始化數據。
[cpp]
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
int father[1000000], flag[1000000];
int findset(int x)//查
{
if(x != father[x])
father[x]=findset(father[x]);//路徑壓縮
return father[x];
}
int unionset(int a, int b)//並
{
int x=findset(a);
int y=findset(b);
if(y != b)//b連接在a上,要保證b是個根節點,否則b將有兩個父節點
return 1;
if(x == y)//如果a,b在同一棵樹中,若再進行並操作就會產生環
return 1;
else
father[y]=x;//若無以上情況,則可以合並兩棵樹
return 0;
}
int main()
{
int a, b, key=0, p=1, i, max=0, t=0;
for(i=1; i<=999999; i++)
father[i]=i;
memset(flag, 0, sizeof(flag));
while(1)
{
scanf("%d%d", &a, &b);
if(a>max) max=a;
if(b>max) max=b;
if(a<=-1 && b<=-1) break;
if(a==0 && b==0)
{
for(i=1; i<=max; i++)
{
if(flag[i]==1 && father[i]==i)
t++;
if(t>=2) break;
}
if(key>0 || t>=2)
printf("Case %d is not a tree.\n", p++);
else
printf("Case %d is a tree.\n", p++);
for(i=1; i<=999999; i++)
father[i]=i;
key=0; t=0; max=0;
memset(flag, 0, sizeof(flag));
continue;
}
flag[a]=1;flag[b]=1;//對輸入的編號標記
key+=unionset(a,b);//若出現不合法的情況,key的值會大於0
}
}