Problem Description
Many geometry(幾何)problems were designed in the ACM/ICPC. And now, I also prepare a geometry problem for this final exam. According to the experience of many ACMers, geometry problems are always much trouble, but this problem is very easy, after all we are now attending an exam, not a contest :)
Give you N (1<=N<=100) segments(線段), please output the number of all intersections(交點). You should count repeatedly if M (M>2) segments intersect at the same point.
Note:
You can assume that two segments would not intersect at more than one point.
Input
Input contains multiple test cases. Each test case contains a integer N (1=N<=100) in a line first, and then N lines follow. Each line describes one segment with four float values x1, y1, x2, y2 which are coordinates of the segment’s ending.
A test case starting with 0 terminates the input and this test case is not to be processed.
Output
For each case, print the number of intersections, and one line one case.
Sample Input
2
0.00 0.00 1.00 1.00
0.00 1.00 1.00 0.00
3
0.00 0.00 1.00 1.00
0.00 1.00 1.00 0.000
0.00 0.00 1.00 0.00
0
Sample Output
1
3
Author
lcy
這道題的主要解題思路如下:
第1 步:快速排斥試驗,如果分別以P1P2 ,P3P4 為對角線做矩形,而這兩個矩形不相交,則這兩條線段肯定不相交,如下左圖;即使兩個矩形相交,這兩條線段也不一定相交,如下右圖,這時再用第2 步判斷;
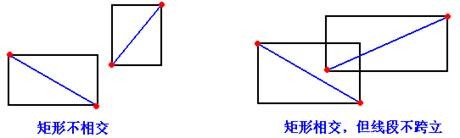
表示成語句,即兩個矩形相交當且僅當下列式子為真:
(max(x1,x2)≥min(x3,x4))∧ (max(x3,x4)≥min(x1,x2)) ∧(max(y1,y2)≥min(y3,y4))∧(max(y3,y4)≥min(y1,y2))
兩個矩形相交必須在兩個方向上都相交,式子的前半部分判斷在x 方向上是否相交,後半部分判斷在y 方向上是否相交。
第2 步:確定每條線段是否“跨立”另一條線段所在的直線。
跨立:如果點P1 處於直線P3P4的一邊,而P2處於該直線的另一邊,則我們說線段p1p2跨立直線P3P4,如果P1 或P2 在直線P3P4 上,也算跨立。
兩條線段相交當且僅當它們能夠通過第1 步的快速排斥試驗,並且每一條線段都跨立另一條線段所在的直線。

具體第2 步的實現,只要用叉積去做就可以了,即只要判斷矢量p1p3和p1p4是否在p1p2的兩邊相對的位置上,如果這樣,則線段p1p2跨立直線P3P4。也即檢查叉積(P3-P1)×(P2-P1)與(P4-P1)×(P2-P1)的符號是否相同,相同則不跨立,線段也就不相交,否則相交。
當然也有一些特殊情況需要處理,如任何一個叉積為0,則P3 或P4 在直線P1P2 上,又因為通過了快速排斥試驗,所以下圖左邊的情況是不可能出現的,只會出現右邊的兩種情況。當然,還會出現一條或兩條線段的長度為0,如果兩條線段的長度都是0,則只要通過快速排斥試驗就能確定;如果僅有一條線段的長度為0,如p3p4的長度為0,則線段相交當且僅當叉積(P3-P1)×(P2-P1)。
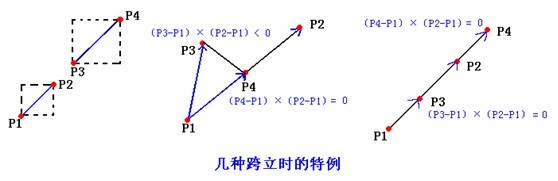
有關於叉積的概念:
矢量的矢量積(叉乘、叉積)
① 矢量積的一般含義:兩個矢量a 和b 的矢量積是一個矢量,記作a×b,其模等於由a 和b作成的平行四邊形的面積,方向與平行四邊形所在平面垂直,當站在這個方向觀察時,a 逆時針轉過一個小於π的角到達b 的方向。這個方向也可以用物理上的右手螺旋定則判斷:右手四指彎向由A 轉到B 的方向(轉過的角小於π),拇指指向的就是矢量積的方向。如下圖(左)。
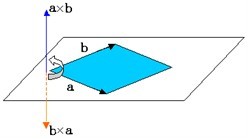
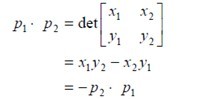
② 我們給出叉積的等價而更有用的定義,把叉積定義為一個矩陣的行列式:
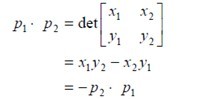
如上右圖,如果 p1 × p2 為正數,則相對原點(0,0)來說, p1 在p 2 的順時針方向; 如果p 1 × p2為負數,則p 1 在p 2 的逆時針方向。如果p 1× p2 =0,則p 1和p 2 模相等且共線,方向相同或相反。
③ 給定兩個矢量:P0P1和P0P2,對它們的公共端點P0來說,判斷P0P1是否在P0P2的順時針方向。
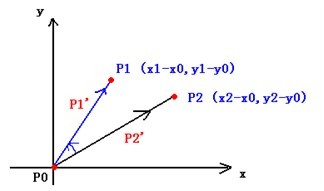
方法:如上圖,把0 p 作為原點,得出向量P1’=P1-P0 和P2’=P2-P0,因此,這兩個向量的叉積為: 如果該叉積為正,則P0P1在P0P2的順時針方向,如果為負,則P0P1在P0P2的逆時針方向。如果等於0,則P0,P1,P2三點共線。
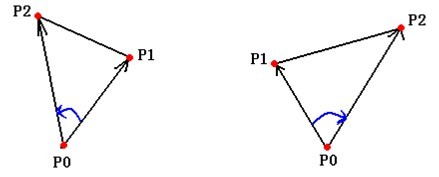
④ 討論另一個重要問題:確定連續線段是向左轉還是向右轉,如下圖,即兩條連續線段P0P1
和P1P2在點P1 是向左轉還是向右轉。也即∠P1P0P2的轉向。
方法:叉積,同上。
這道題還要注意一點:
//剛開始做題,先水幾道題,鞏固鞏固狀態
//粗枝大葉的老毛病又犯了,一定要細致
#include<iostream>
using namespace std;
struct Coord//坐標
{
double x,y;
};
struct Segment//一條直線上的兩個點
{
Coord a,b;
};
bool Judge(Coord &a,Coord &b,Coord &c,Coord &d)
{
if(!(min(a.x,b.x)<=max(c.x,d.x) && min(c.y,d.y)<=max(a.y,b.y)&&
min(c.x,d.x)<=max(a.x,b.x) && min(a.y,b.y)<=max(c.y,d.y)))//這裡的確如此,這一步是判定兩矩形是否相交
//特別要注意一個矩形含於另一個矩形之內的情況
return false;
double u,v,w,z;//分別記錄兩個向量
u=(c.x-a.x)*(b.y-a.y)-(b.x-a.x)*(c.y-a.y);
v=(d.x-a.x)*(b.y-a.y)-(b.x-a.x)*(d.y-a.y);
w=(a.x-c.x)*(d.y-c.y)-(d.x-c.x)*(a.y-c.y);
z=(b.x-c.x)*(d.y-c.y)-(d.x-c.x)*(b.y-c.y);
return (u*v<=0.00000001 && w*z<=0.00000001);
}
int main()
{
int n;
Segment str[101];
while(cin>>n && n!=0)
{
int count=0;
for(int i=0;i<n;i++)
{
cin>>str[i].a.x>>str[i].a.y>>str[i].b.x>>str[i].b.y;
}
for(int i=0;i<n;i++)
for(int j=i+1;j<n;j++)
if(Judge(str[i].a,str[i].b,str[j].a,str[j].b)) count++;
cout<<count<<endl;
}
return 0;
}
還有一些情況要考慮:
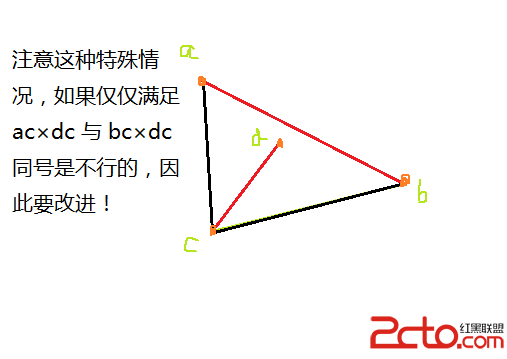
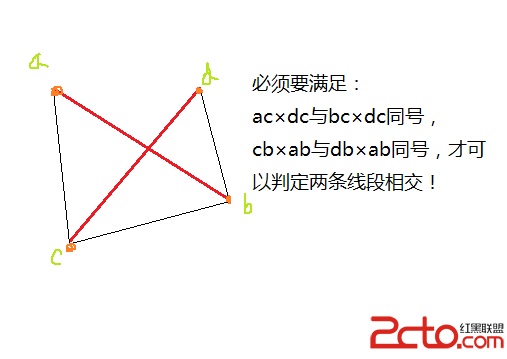
就這樣!