上一篇博文主要對樹、二叉樹的概念及其一些基本特性進行簡要的描述,偏向於理論知識。而本文的主要內容是針對二叉樹這種數據結構的實現細節進行設計與分析,理論與實踐相結合可以加深對系統知識的掌握。二叉樹這種數據結構,應用非常廣泛,在linux內核中隨處可見,因此,如果能夠熟練的掌握這項技能,將有助於理解其它系統。
一、“初識”二叉樹
在代碼的實現中,二叉樹究竟是什麼?請看下面代碼:
[cpp]
/*
* filename: bitree.h
* author: zhm
* date: 2012-01-08
*/
#ifndef BITREE_H
#define BITREE_H
#include <stdlib.h>
/* define a binary tree node */
typedef struct BiTreeNode_
{
void *data;
struct BiTreeNode_ *left; //point to left node.
struct BiTreeNode_ *right; //point to right node.
}BiTreeNode;
這是一段關於二叉樹結點的數據結構,一共有3個域,數據域和左右指針域,數據域包含了二叉樹每個結點的關鍵信息,左右指針域分別指向它的左右孩子結點。
[html]
/* define a binary tree */
typedef struct BiTree_
{
int size; //number of the elements in the tree.
BiTreeNode *root; //root node.
int (*compare)(const void *key1, const void *key2);
void (*destroy)(void *data);
}BiTree;
這裡定義了一個結構體,這個結構體就是一棵二叉樹了。因為它維護了一棵二叉樹的重要信息,如,二叉樹中結點總數size,根結點的位置root,結點數據信息的比較操作,銷毀二叉樹的destroy函數等。可以通過這個結構體的root域就可以方便的按深度及廣度遍歷整個二叉樹,尋找到任何一個結點了。
二、“深入”二叉樹
二叉樹究竟是如何建立的?凡事產生均有一個過程,二叉樹的建立也有一個過程。它是由不同的結點組成,按照實際情況逐一將這些結點插入從而形成二叉樹,當然,也面臨著結點的刪除操作等,總而言之,它有以下基本操作(接口):
[cpp]
/* public interface */
void bitree_init( BiTree *tree, void (*destroy)(void *data) );
void bitree_destroy(BiTree *tree);
int bitree_ins_left(BiTree *tree, BiTreeNode *node, const void *data);
int bitree_ins_right(BiTree *tree, BiTreeNode *node, const void *data);
void bitree_rem_left(BiTree *tree, BiTreeNode *node);
void bitree_rem_right(BiTree *tree, BiTreeNode *node);
int bitree_merge(BiTree *merge, BiTree *left, BiTree *right, const void *data);
#define bitree_size(tree) ((tree)->size) //獲取大小
#define bitree_root(tree) ((tree)->root) //獲取根結點
#define bitree_is_eob(node) ((node) == NULL) //判斷分支是否結束
#define bitree_is_leaf(node) ((node)->left == NULL && (node)->right == NULL) //判斷是否是葉子結點
#define bitree_data(node) ((node)->data) //獲取數據域
#define bitree_left(node) ((node)->left) //獲取左結點(左孩子)
#define bitree_right(node) ((node)->right)//獲取右結點(右孩子)
#endif
1 二叉樹的初始化(bitree_init):此操作完成後,一棵空的二叉樹就建立了,此時它沒有任何結點,這是二叉樹進行後續操作的前提。
2 二叉樹的銷毀(bitree_destroy):此操作用於銷毀一棵二叉樹
3 二叉樹插入操作(bitree_ins_left):將data中的信息插入到當前node結點的左指針域,成為當前node結點的左孩子。當node為NULL時,從根結點位置插入。
4二叉樹插入操作(bitree_ins_right):同3,不同的是其插入的是右指針域。
5 二叉樹刪除操作(bitree_rem_left):刪除以node結點為根的子樹的左子樹。當node = NULL時,則為刪除整棵二叉樹
6二叉樹刪除操作(bitree_rem_right):同5,不同的是其刪除的是右子樹。
7 二叉樹的合並(bitree_merge):將兩棵二叉樹,分別合並成以data域為根的新二叉樹,原來這兩棵二叉樹分別成為新二叉樹的左右子樹。
8其它宏定義:代碼中已經說明清楚,這裡不再累述。
9二叉樹的三種遍歷操作:先序遍歷、中序遍歷和後序遍歷。(放在後面說明)
三、實現二叉樹
1、二叉樹初始化的實現(bitree_init)
[cpp]
/*
* filename: bitree.c
* author: zhm
* date: 2012-01-08
*/
#include <string.h>
#include <stdlib.h>
#include "bitree.h"
/* bitree_init */
void bitree_init( BiTree *tree, void (*destroy)(void *data) )
{
/* Initialize the binary tree */
tree->size = 0;
tree->root = NULL;
tree->destroy = destroy;
return;
}
完成對維護二叉樹結構體的各域值的初始化。
2、二叉樹的銷毀操作(bitree_destroy)
[cpp]
/* bitree_destroy */
void bitree_destroy(BiTree *tree)
{
/* Remove all the nodes from the tree */
bitree_rem_left(tree, NULL);
memset(tree, 0, sizeof(BiTree) );
return;
}
先刪除二叉樹的所有結點,然後清空二叉樹結構體。
3、二叉樹插入操作(bitree_ins_left及bitree_ins_right)
先是插入左子樹操作:
[cpp]
/* bitree_ins_left */
int bitree_ins_left(BiTree *tree, BiTreeNode *node, const void *data)
{
BiTreeNode *new_node, **position;
if( node == NULL )
{
if( bitree_size(tree) > 0 )
return -1;
position = &tree->root;
}
else
{
if( bitree_left(node) != NULL )
return -1;
position = &node->left;
}
/* Allocate storage for the node */
new_node = (BiTreeNode *)malloc(sizeof(BiTreeNode));
if( new_node == NULL )
return -1;
/* insert the node into the tree */
new_node->data = (void *)data;
new_node->left = NULL;
new_node->right = NULL;
*position = new_node;
tree->size++;
return 0;
}
接著是插入右子樹操作:
[cpp]
/* bitree_ins_right */
int bitree_ins_right(BiTree *tree, BiTreeNode *node, const void *data)
{
BiTreeNode *new_node, **position;
if( node == NULL )
{
if( bitree_size(tree) > 0 )
return -1;
position = &tree->root;
}
else
{
if( bitree_right(node) != NULL )
return -1;
position = &node->right;
}
/* allocate the storage for the node. */
new_node = (BiTreeNode *)malloc(sizeof(BiTreeNode));
if( new_node == NULL )
return -1;
new_node->data = (void *)data;
new_node->left = NULL;
new_node->right = NULL;
*position = new_node;
tree->size++;
return 0;
}
通過代碼可以看出,這兩個函數的實現幾乎一樣,我們這裡只需要學會其內在思想:
(1) 找准需要插入的位置:是在根結點位置,當前結點的左指針還是右指針位置。
(2) 分配新結點,在適當的地方插入結點: *position = new_node完成了這個插入操作
(3) 更新二叉樹size域。
4、二叉樹刪除操作(bitree_rem_left及bitre_rem_right)
先是刪除左子樹操作:
[cpp]
/* bitree_rem_left */
void bitree_rem_left(BiTree *tree, BiTreeNode *node)
{
BiTreeNode **position;
/* Do not allow removal from an empty tree. */
if( bitree_size(tree) == 0 )
return;
if( node == NULL )
{
position = &tree->root;
}
else
{
position = &node->left;
}
/* Remove the nodes. */
if( *position != NULL )
{
bitree_rem_left(tree, *position);
bitree_rem_right(tree, *position);
if( tree->destroy != NULL )
{
tree->destroy((*position)->data);
}
free(*position);
*position = NULL;
/* adjust the size */
tree->size--;
}
return;
}
接著是刪除右子樹操作:
[cpp]
/* bitree_rem_right */
void bitree_rem_right(BiTree *tree, BiTreeNode *node)
{
BiTreeNode **position;
if( bitree_size(tree) == 0 )
return;
if( node == NULL )
{
position = &tree->root;
}
else
{
position = &node->right;
}
/* Remove the nodes */
if( *position != NULL )
{
bitree_rem_left(tree, *position);
bitree_rem_right(tree, *position);
if( tree->destroy != NULL )
{
tree->destroy((*position)->data);
}
free(*position);
*position = NULL;
tree->size--;
}
return;
}
同樣的,我們需要掌握其實現的思想:
通過采用遞歸的思想,後序遍歷逐層深入到最底層(深度優先搜索),從下至上逐一刪除各個結點,釋放被刪除結點的數據域空間,更新二叉樹size值大小。注意遞歸退出的條件:
(1) 樹為空時退出
(2) *Position為空時退出
可以思考:為何刪除操作不能采用前序或中序遍歷?
5、二叉樹的合並(bitree_merge)
[cpp]
/* bitree_merge */
int bitree_merge(BiTree *merge, BiTree *left, BiTree *right, const void *data)
{
/* Initialize the merged tree. */
bitree_init(merge, left->destroy);
/* Insert the data for the root node of the merged tree */
if( bitree_ins_left(merge, NULL, data) != 0 )
{
bitree_destroy(merge);
return -1;
}
/* Merge the two binary trees into a single binary tree */
bitree_root(merge)->left = bitree_root(left);
bitree_root(merge)->right = bitree_root(right);
/* Adjust the size of the new tree */
merge->size = merge->size + bitree_size(left) + bitree_size(right);
/* Do not let the original trees access the merged nodes. */
left->root = NULL;
left->size = 0;
right->root = NULL;
right->size = 0;
return 0;
}
二叉樹的合並操作非常簡單,有以下幾個步驟:
(1) 初始化新二叉樹,並插入data域成為新二叉樹的根結點
(2) 新二叉樹的左指針指向左子樹的根結點
(3) 新二叉樹的右指針指向右子樹的根結點
(4) 新二叉樹結點個數 =左、右子樹結點之和+1
(5) 對原左、右子樹結構體相關域的清空操作。
四、遍歷二叉樹
遍歷二叉樹是指按照一定的規律,對二叉樹的每個結點訪問且僅訪問一次的處理過程。這裡的“訪問”是泛指對結點數據的某種處理操作,如可以是printf打印顯示,可以是鏈表的插入操作,也可以是某些數學運算,等等。
遍歷的目的:通過一次遍歷後,可以使樹中結點的非線性結構按訪問的先後順序轉變為某種線性序列。如:可以按照訪問的先後順序將數據域逐一填入某一數組中,當然,也可以插入某個鏈表中,然後通過鏈表的方式對數據域進行訪問。
遍歷的次序: DLR先序遍歷、LDR中序遍歷、LRD後序遍歷
可以看出,先、中、後序的遍歷主要根據根結點的訪問次序命名,而L左結點總是先於R右結點訪問。無論是哪種遍歷方式,其核心的思想是總是遞歸,以中序遍歷二叉樹為例,說明其算法思想:
若二叉樹非空,則:
1)中序遍歷左子樹
2)訪問根結點
3)中序遍歷右子樹
(1)先序遍歷二叉樹
[cpp]
/* preorder */
int preorder(const BiTreeNode *node, List *list)
{
if( !bitree_is_eob(node) )
{
if( list_ins_next(list, list_tail(list), bitree_data(node) ) != 0 )
{
return -1;
}
if( !bitree_is_eob( bitree_left(node) ) )
{
if( preorder(bitree_left(node), list) != 0 )
return -1;
}
if( !bitree_is_eob( bitree_right(node) ) )
{
if( preorder(bitree_right(node), list) != 0 )
return -1;
}
}
return 0;
}
(2)中序遍歷二叉樹
[html]
/* inorder */
int inorder(const BiTreeNode *node, List *list)
{
if( !bitree_is_eob(node) )
{
if( !bitree_is_eob(bitree_left(node)) )
{
if( inorder( bitree_left(node), list ) != 0 )
return -1;
}
if( list_ins_next(list, list_tail(list), bitree_data(node)) != 0 )
{
return -1;
}
if( !bitree_is_eob(bitree_right(node)) )
{
if( inorder( bitree_right(node), list ) != 0 )
return -1;
}
}
return 0;
}
(3)後序遍歷二叉樹
[cpp]
/* postorder */
int postorder(const BiTreeNode *node, List *list)
{
if( !bitree_is_eob(node) )
{
if( !bitree_is_eob(bitree_left(node)) )
{
if( postorder(bitree_left(node), list) != 0 )
return -1;
}
if( !bitree_is_eob(bitree_right(node)) )
{
if( postorder(bitree_right(node), list) != 0 )
return -1;
}
if( list_ins_next(list, list_tail(list), bitree_data(node)) != 0 )
return -1;
}
return 0;
}
在本例的三種遍歷代碼中,“訪問”的方式是將結點的數據域插入至某一鏈表結構中。
五、二叉樹簡單應用
對上述所有二叉樹的代碼如果未進行使用或驗證,無疑是一些基本符號,沒有任何的意義,所以本節主要對前面二叉樹的各個接口進行簡單的應用測試,在進入實際的應用之前,有幾個函數需要先實現,如下:
[cpp]
/* destroy */
void destroy(void *data)
{
free(data);
return;
}
這是創建銷毀函數的代碼,在bitree_init()初始化二叉樹時需要傳遞它的函數入口地址。接著是創建二叉樹的函數:
[cpp]
/* create_tree */
int create_tree(BiTree *tree, BiTreeNode *node)
{
int ret;
int *int_ptr = NULL;
char ch;
scanf("%c", &ch);
if( ch == '#' )
{
return 0;
}
int_ptr = (int *)malloc(sizeof(int));
if( int_ptr == NULL )
return -1;
*int_ptr = ch-48;
if( node == NULL )
{
bitree_init(tree, destroy);
ret = bitree_ins_left(tree, NULL, (void *)int_ptr);
if( ret != 0 )
{
free(int_ptr);
return -1;
}
printf("root is %d\n", *(int *)bitree_data(tree->root));
create_tree(tree, tree->root);
}
else
{
//insert the data into left tree
ret = bitree_ins_left(tree, node, (void *)int_ptr);
if( ret != 0 )
{
free(int_ptr);
return -1;
}
printf("node: %d 's left node is :%d\n", *(int *)bitree_data(node), *(int *)bitree_data(node->left));
ret = create_tree(tree, node->left);
scanf("%c", &ch);
if( ch == '#')
return 0;
int_ptr = (int *)malloc(sizeof(int));
if( int_ptr == NULL )
return -1;
*int_ptr = ch-48;
// insert the data into right tree.
ret = bitree_ins_right(tree, node, (void *)int_ptr);
if( ret != 0 )
{
free(int_ptr);
return -1;
}
printf("node: %d 's right node is :%d\n", *(int *)bitree_data(node), *(int *)bitree_data(node->right));
ret = create_tree(tree, node->right);
}
return 0;
}
它的實現邏輯比較簡單,在於采用遞歸的思想來創建一棵二叉樹,並且其遞歸退出的條件是輸入“#”符號,注意:本代碼的實現只能插入簡單的數字(范圍0-9),這對於簡單測試來說已經足夠了。
下面是具體的關於二叉樹各接口代碼的簡單測試應用,如下:
[cpp]
/* main */
int main(int argc, char **argv)
{
int ret;
int *int_ptr;
BiTree tree1, tree2, tree_merge;
List list;
ListElmt *member;
BiTreeNode *nd;
/* tree1 as follows :
1
/ \
2 5
/ \ / \
3 4 6 7
*/
create_tree(&tree1, NULL); //input "123#4#56#7#"
printf("\nstep1:tree1 build success\n");
/* tree2 as follows:
0
/ \
8 9
/ \ /
6 7 3
*/
int_ptr = NULL;
create_tree(&tree2, NULL); //input "086#7#93###"
printf("step2:tree2 build success\n");
int_ptr = (int *)malloc(sizeof(int));
if( int_ptr == NULL )
return -1;
*int_ptr = 11;
/* after merged as follow( by tree1 and tree2 ) :
11
/ \
1 0
/ \ / \
2 5 8 9
/ \ / \ / \ / \
3 4 6 9 6 7 3 NULL
*/
ret = bitree_merge(&tree_merge, &tree1, &tree2, int_ptr);
printf("step3: after merged: there are %d number nodes in the tree_merge.\n", bitree_size(&tree_merge));
/* after remove the right tree:
11
/ \
1 NULL
/ \
2 5
/ \ / \
3 4 6 7
*/
printf("\nstep4: remove the right tree in tree_merge.\n");
bitree_rem_right(&tree_merge, bitree_root(&tree_merge) );
printf("after remove the right tree, there are %d number nodes in the tree_merge.\n", bitree_size(&tree_merge));
printf("\nstep5: preorder traverse the tree and insert the nodes into the list\n");
list_init(&list, destroy);
ret = preorder( bitree_root(&tree_merge), &list );
printf("according to the sequence of the preorder traversing the tree:\n");
for(member = list_head(&list); member != NULL; member = list_next(member) )
{
printf("%d ", *(int *)list_data(member));
}
printf("\n");
printf("\nsetp6: inorder traverse the tree and insert the nodes into the list\n");
list_init(&list, destroy);
ret = inorder( bitree_root(&tree_merge), &list );
printf("according to the sequence of the inorder traversing the tree:\n");
for(member = list_head(&list); member != NULL; member = list_next(member) )
{
printf("%d ", *(int *)list_data(member));
}
printf("\n");
printf("\nsetp7: postorder traverse the tree and insert the nodes into the list\n");
list_init(&list, destroy);
ret = postorder( bitree_root(&tree_merge), &list );
printf("according to the sequence of the postorder traversing the tree:\n");
for(member = list_head(&list); member != NULL; member = list_next(member) )
{
printf("%d ", *(int *)list_data(member));
}
printf("\n");
printf("\nstep8: delete all the nodes in the tree.\n");
bitree_rem_left( &tree_merge, NULL );
printf("there are %d number nodes.\n", bitree_size(&tree_merge) );
bitree_destroy(&tree_merge);
return 0;
}
具體的含義不再說明,注釋以及printf已經非常詳細。代碼的編譯過程如下:
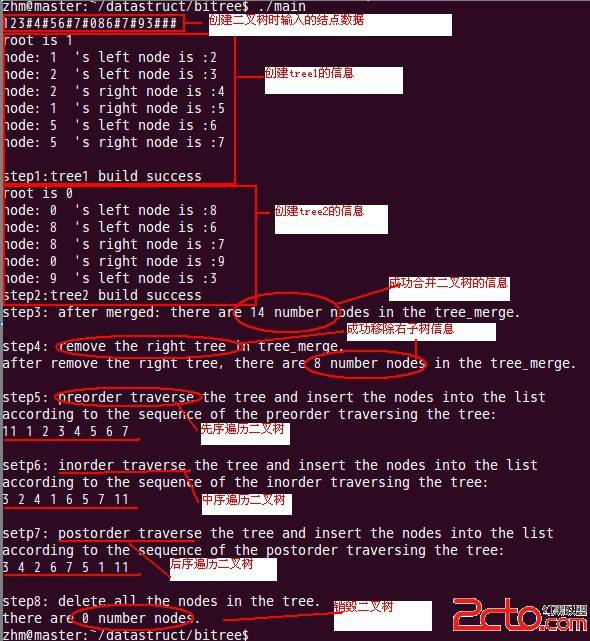
 程序執行過程如下:
程序執行過程如下: