Cube
Problem Description
Cowl is good at solving math problems. One day a friend asked him such a question: You are given a cube whose edge length is N, it is cut by the planes that was paralleled to its side planes into N * N * N unit cubes. Two unit cubes may have no common points or two common points or four common points. Your job is to calculate how many pairs of unit cubes that have no more than two common points.
Process to the end of file.
Input
There will be many test cases. Each test case will only give the edge length N of a cube in one line. N is a positive integer(1<=N<=30).
Output
For each test case, you should output the number of pairs that was described above in one line.
Sample Input
1
2
3
Sample Output
0
16
297
Hint
Hint
The results will not exceed int type.
Author
Gao Bo
Source
杭州電子科技大學第三屆程序設計大賽
Recommend
Ignatius.L
這純粹是一道數學題目，推理如下：
給你一個正方體，切割成單位體積的小正方體，求所有公共頂點數<=2的小正方體的對數。
公共點的數目只可能有：0,1,2,4.
很明顯我們用總的對數減掉有四個公共點的對數就可以了。
總的公共點對數：n^3*(n^3-1)/2(一共有n^3塊小方塊，從中選出2塊)（只有兩個小方塊之間才存在公共點，我們從所有的小方塊中任意選出兩個，自然就確定了這兩個小方塊的公共點的對數，從所有小方塊中任意選取兩個，總得選取方法數就是所有種類對數數目的總和！）
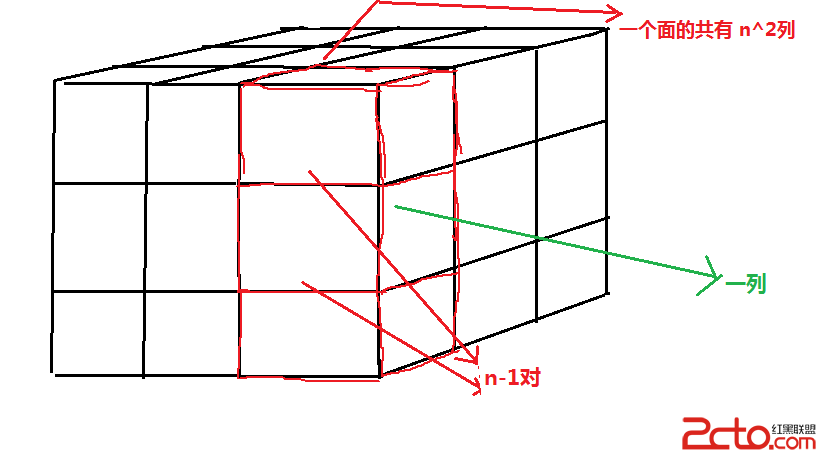
公共點為4的對數：一列有n-1對（n個小方塊，相鄰的兩個為一對符合要求），一個面的共有 n^2列，底面和左面，前面三個方向相同，同理可得，故總數為：3*n^2(n-1)
所以結果為：n^3 * (n^3-1) - 3*n^2(n-1)
代碼如下：
[cpp]
#include<iostream>
using namespace std;
int main()
{
int num,sum;
while(scanf("%d",&num)!=EOF)
{
sum=num*num*num*(num*num*num-1)/2-3*num*num*(num-1);
cout<<sum<<endl;
}
return 0;
}
