第一章 關於數據結構
1.數據結構研究什麼?(計算機加工的對象由數值——>非數值)
將現實生活中大量而復雜的問題(非數值問題)以特定的數據類型(邏輯結構)和特定的存儲結構(物理結構)保存到主存儲器中,以及在此基礎上為實現某個功能(刪除、排序)相對應的操作。
2.數據的邏輯結構:
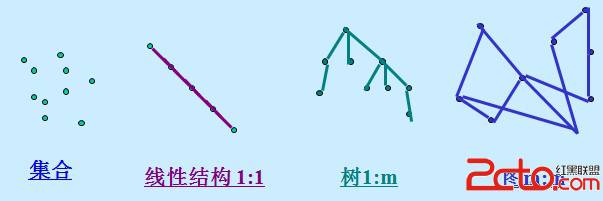 3.存儲結構(物理結構):
1)順序存儲結構(借助元素在存儲器中的相對位置)
2)鏈式存儲結構(借助元素存儲地址的指針)
4.抽象數據類型ADT:
[cpp]
ADT抽象數據類型名
{
數據對象:<數據對象的定義>
數據關系:<數據對象之間關系的定義>
基本操作:<基本操作的定義>
}
5、時間復雜度:
取決定性作用語句的重復次數
第二章 線性表
1.線性結構的基本特征:
1)集合中必存在唯一的一個“第一個元素”;
2)集合中必存在唯一的一個“最後元素”;
3)除最後元素外,均有唯一的後繼;
4)除第一元素之外,均有唯一的前驅;
2.ADT
[cpp]
ADT List
{
數據對象:D={ a1,a2, a3, ... an};
數據關系:R={<a1, a2>, <a2, a3>, <a3, a4> … <an-1, an>};
基本操作:
InitList(&L); //操作結果:構造線性表;
DestroyList(&L); //操作結果:銷毀線性表;
ListEmpty(L); //操作結果:若L為空表,則返回TRUE,否則FALSE;
ListLength(L); //操作結果:返回L中元素個數;
PriorElem(L,cur_e,&pre_e)//操作結果:cur_e是L的元素,但不是第一個
//則用pre_e返回它的前驅。若操作失敗,pre_e無定義
NextElem(L,cur_e,&next_e)//操作結果:cur_e是L的元素,但不是最後一個,
//則用next_e返回它的後繼。若操作失敗,next_e無定義
GetElem(L,i,&e) // 1<= i <=LengthList(L) 操作結果:用e返回L中第i個元素的值。
LocateElem(L,e,compare())//compare()是元素判定函數。返回L中第一個與e滿足compare()的元素位序。
//若這樣的元素不存在,則返回值為0。
ListTraverse(L,visit( )) //依次對L的每個元素調用函數visit( ).一旦visit( )失敗,則操作失敗
ClearList(&L) //操作結果將L重置為空表。
PutElem(L,i,&e) //1<=i<=LengthList(L) 結果:L中第i個元素賦值為e
ListInsert(&L,i,e) //1<=i <=LengthList(L) +1 結果:在L的第i個元素之前插入新的元素e,L的長度增1
ListDelete(&L,i,&e)//1<=i <=LengthList(L) 結果:刪除L的第i個元素,並用e返回其值,,L的長度減1
}ADT List
3.順序實現
1)存儲結構:
3.存儲結構(物理結構):
1)順序存儲結構(借助元素在存儲器中的相對位置)
2)鏈式存儲結構(借助元素存儲地址的指針)
4.抽象數據類型ADT:
[cpp]
ADT抽象數據類型名
{
數據對象:<數據對象的定義>
數據關系:<數據對象之間關系的定義>
基本操作:<基本操作的定義>
}
5、時間復雜度:
取決定性作用語句的重復次數
第二章 線性表
1.線性結構的基本特征:
1)集合中必存在唯一的一個“第一個元素”;
2)集合中必存在唯一的一個“最後元素”;
3)除最後元素外,均有唯一的後繼;
4)除第一元素之外,均有唯一的前驅;
2.ADT
[cpp]
ADT List
{
數據對象:D={ a1,a2, a3, ... an};
數據關系:R={<a1, a2>, <a2, a3>, <a3, a4> … <an-1, an>};
基本操作:
InitList(&L); //操作結果:構造線性表;
DestroyList(&L); //操作結果:銷毀線性表;
ListEmpty(L); //操作結果:若L為空表,則返回TRUE,否則FALSE;
ListLength(L); //操作結果:返回L中元素個數;
PriorElem(L,cur_e,&pre_e)//操作結果:cur_e是L的元素,但不是第一個
//則用pre_e返回它的前驅。若操作失敗,pre_e無定義
NextElem(L,cur_e,&next_e)//操作結果:cur_e是L的元素,但不是最後一個,
//則用next_e返回它的後繼。若操作失敗,next_e無定義
GetElem(L,i,&e) // 1<= i <=LengthList(L) 操作結果:用e返回L中第i個元素的值。
LocateElem(L,e,compare())//compare()是元素判定函數。返回L中第一個與e滿足compare()的元素位序。
//若這樣的元素不存在,則返回值為0。
ListTraverse(L,visit( )) //依次對L的每個元素調用函數visit( ).一旦visit( )失敗,則操作失敗
ClearList(&L) //操作結果將L重置為空表。
PutElem(L,i,&e) //1<=i<=LengthList(L) 結果:L中第i個元素賦值為e
ListInsert(&L,i,e) //1<=i <=LengthList(L) +1 結果:在L的第i個元素之前插入新的元素e,L的長度增1
ListDelete(&L,i,&e)//1<=i <=LengthList(L) 結果:刪除L的第i個元素,並用e返回其值,,L的長度減1
}ADT List
3.順序實現
1)存儲結構:
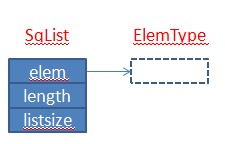 [cpp]
#define LIST_INIT_SIZE 10
#define INCREAMENT 2
struct SqList
{
ElemType * elem;
int length;
int listsize;
};
2)基本操作
[cpp]
void InitList(SqList & L )
{
L.elem = (ElemType *)malloc(LIST_INIT_SIZE*sizeof(ElemType) );
L.length = 0;
L.listsize = LIST_INIT_SIZE;
}
void DestroyList(SqList & L)
{
free(L.elem);
L.elem = NULL;
L.length = 0;
L.listsize = 0;
}
void ClearList( SqList & L)
{
L.length = 0;
}
Status ListEmpty( SqList L)
{
if( L.length != 0 )
return FALSE;
else
return TRUE;
}
int ListLength(SqList L)
{
return L.length;
}
Status GetElem(SqList L, int i , ElemType & e)
{
if( i < 1 || i > L.length )
return ERROR;
e = *(L.elem + i - 1);
return OK;
}
int LocateElem(SqList L,ElemType e, Status(*compare)(ElemType , ElemType))
{
ElemType * p;
p = L.elem;
int i = 1;
while(i < L.length && !(compare(e, *p)))
{
i++;
p++;
}
if( i< L.length)
return i;
else
return 0;
}
Status PriorElem(SqList L, ElemType cur_e, ElemType & pre_e)
{
ElemType * p;
p = L.elem + 1; //p 和 i 之間進行合作
int i = 2;
while(i < L.length && *p!=cur_e)
{
i++;
p++;
}
if( i< L.length)
{
pre_e = *(--p);
return OK;
}
else
return INFEASIBLE;
}
Status NextElem(SqList L,ElemType cur_e,ElemType &next_e)
{ // 初始條件:順序線性表L已存在
// 操作結果:若cur_e是L的數據元素,且不是最後一個,則用next_e返回它的後繼,
// 否則操作失敗,next_e無定義
int i=1;
ElemType *p=L.elem;
while(i<L.length&&*p!=cur_e)
{
i++;
p++;
}
if(i==L.length)
return INFEASIBLE; // 操作失敗
else
{
next_e=*++p;
return OK;
}
}
Status ListInsert(SqList & L, int i , ElemType e)
{
if(i < 1 || i > L.length + 1)
return ERROR;
ElemType * newbase;
if(L.length >= L.listsize)
{
newbase = (ElemType *)realloc(L.elem,( L.listsize + INCREAMENT) * sizeof(ElemType));
L.listsize = L.listsize + INCREAMENT;
if(!newbase)
exit(OVERFLOW);
L.elem = newbase;
}
ElemType * p,*q;
p = L.elem + L.length -1;
q = L.elem + i -1;
for(p = L.elem + L.length -1; p >= q; --p)
{
*(p + 1) = * p;
}
*q = e;
L.length = L.length + 1;
return OK;
}
Status ListDelete(SqList &L,int i,ElemType &e) // 算法2.5
{ // 初始條件:順序線性表L已存在,1≤i≤ListLength(L)
// 操作結果:刪除L的第i個數據元素,並用e返回其值,L的長度減1
ElemType *p,*q;
if(i<1||i>L.length) // i值不合法
return ERROR;
p=L.elem+i-1; // p為被刪除元素的位置
e=*p; // 被刪除元素的值賦給e
q=L.elem+L.length-1; // 表尾元素的位置
for(++p;p<=q;++p) // 被刪除元素之後的元素左移
*(p-1)=*p;
L.length--; // 表長減1
return OK;
}
void ListTraverse(SqList L,void(*vi)(ElemType & ))
{ // 初始條件:順序線性表L已存在
// 操作結果:依次對L的每個數據元素調用函數vi()
// vi()的形參加'&',表明可通過調用vi()改變元素的值
ElemType *p;
int i;
p=L.elem;
for(i=1;i<=L.length;i++)
vi(*p++);
printf("\n");
}
4.鏈式實現
[cpp]
#define LIST_INIT_SIZE 10
#define INCREAMENT 2
struct SqList
{
ElemType * elem;
int length;
int listsize;
};
2)基本操作
[cpp]
void InitList(SqList & L )
{
L.elem = (ElemType *)malloc(LIST_INIT_SIZE*sizeof(ElemType) );
L.length = 0;
L.listsize = LIST_INIT_SIZE;
}
void DestroyList(SqList & L)
{
free(L.elem);
L.elem = NULL;
L.length = 0;
L.listsize = 0;
}
void ClearList( SqList & L)
{
L.length = 0;
}
Status ListEmpty( SqList L)
{
if( L.length != 0 )
return FALSE;
else
return TRUE;
}
int ListLength(SqList L)
{
return L.length;
}
Status GetElem(SqList L, int i , ElemType & e)
{
if( i < 1 || i > L.length )
return ERROR;
e = *(L.elem + i - 1);
return OK;
}
int LocateElem(SqList L,ElemType e, Status(*compare)(ElemType , ElemType))
{
ElemType * p;
p = L.elem;
int i = 1;
while(i < L.length && !(compare(e, *p)))
{
i++;
p++;
}
if( i< L.length)
return i;
else
return 0;
}
Status PriorElem(SqList L, ElemType cur_e, ElemType & pre_e)
{
ElemType * p;
p = L.elem + 1; //p 和 i 之間進行合作
int i = 2;
while(i < L.length && *p!=cur_e)
{
i++;
p++;
}
if( i< L.length)
{
pre_e = *(--p);
return OK;
}
else
return INFEASIBLE;
}
Status NextElem(SqList L,ElemType cur_e,ElemType &next_e)
{ // 初始條件:順序線性表L已存在
// 操作結果:若cur_e是L的數據元素,且不是最後一個,則用next_e返回它的後繼,
// 否則操作失敗,next_e無定義
int i=1;
ElemType *p=L.elem;
while(i<L.length&&*p!=cur_e)
{
i++;
p++;
}
if(i==L.length)
return INFEASIBLE; // 操作失敗
else
{
next_e=*++p;
return OK;
}
}
Status ListInsert(SqList & L, int i , ElemType e)
{
if(i < 1 || i > L.length + 1)
return ERROR;
ElemType * newbase;
if(L.length >= L.listsize)
{
newbase = (ElemType *)realloc(L.elem,( L.listsize + INCREAMENT) * sizeof(ElemType));
L.listsize = L.listsize + INCREAMENT;
if(!newbase)
exit(OVERFLOW);
L.elem = newbase;
}
ElemType * p,*q;
p = L.elem + L.length -1;
q = L.elem + i -1;
for(p = L.elem + L.length -1; p >= q; --p)
{
*(p + 1) = * p;
}
*q = e;
L.length = L.length + 1;
return OK;
}
Status ListDelete(SqList &L,int i,ElemType &e) // 算法2.5
{ // 初始條件:順序線性表L已存在,1≤i≤ListLength(L)
// 操作結果:刪除L的第i個數據元素,並用e返回其值,L的長度減1
ElemType *p,*q;
if(i<1||i>L.length) // i值不合法
return ERROR;
p=L.elem+i-1; // p為被刪除元素的位置
e=*p; // 被刪除元素的值賦給e
q=L.elem+L.length-1; // 表尾元素的位置
for(++p;p<=q;++p) // 被刪除元素之後的元素左移
*(p-1)=*p;
L.length--; // 表長減1
return OK;
}
void ListTraverse(SqList L,void(*vi)(ElemType & ))
{ // 初始條件:順序線性表L已存在
// 操作結果:依次對L的每個數據元素調用函數vi()
// vi()的形參加'&',表明可通過調用vi()改變元素的值
ElemType *p;
int i;
p=L.elem;
for(i=1;i<=L.length;i++)
vi(*p++);
printf("\n");
}
4.鏈式實現
 1)存儲結構:
[cpp]
struct LNode
{
ElemType data;
LNode * next;
};
typedef LNode * LinkList ;
2)基本操作:
[cpp]
void InitList(LinkList &L)
{ // 操作結果:構造一個空的線性表L
L=(LinkList)malloc(sizeof(LNode)); // 產生頭結點,並使L指向此頭結點
if(!L) // 存儲分配失敗
exit(OVERFLOW);
L->next=NULL; // 指針域為空
}
void DestroyList(LinkList &L)
{ // 初始條件:線性表L已存在。操作結果:銷毀線性表L
LinkList q;
while(L)
{
q=L->next;
free(L);
L=q;
}
}
void ClearList(LinkList L) // 不改變L
{ // 初始條件:線性表L已存在。操作結果:將L重置為空表
LinkList p,q;
p=L->next; // p指向第一個結點
while(p) // 沒到表尾
{
q=p->next;
free(p);
p=q;
}
L->next=NULL; // 頭結點指針域為空
}
Status ListEmpty(LinkList L)
{ // 初始條件:線性表L已存在。操作結果:若L為空表,則返回TRUE,否則返回FALSE
if(L->next) // 非空
return FALSE;
else
return TRUE;
}
int ListLength(LinkList L)
{ // 初始條件:線性表L已存在。操作結果:返回L中數據元素個數
int i=0;
LinkList p=L->next; // p指向第一個結點
while(p) // 沒到表尾
{
i++;
p=p->next;
}
return i;
}
Status GetElem(LinkList L,int i,ElemType &e) // 算法2.8
{ // L為帶頭結點的單鏈表的頭指針。當第i個元素存在時,其值賦給e並返回OK,否則返回ERROR
int j=1; // j為計數器
LinkList p=L->next; // p指向第一個結點
while(p&&j<i) // 順指針向後查找,直到p指向第i個元素或p為空
{
p=p->next;
j++;
}
if(!p||j>i) // 第i個元素不存在
return ERROR;
e=p->data; // 取第i個元素
return OK;
}
int LocateElem(LinkList L,ElemType e,Status(*compare)(ElemType,ElemType))
{ // 初始條件: 線性表L已存在,compare()是數據元素判定函數(滿足為1,否則為0)
/*操作結果: 返回L中第1個與e滿足關系compare()的數據元素的位序。
若這樣的數據元素不存在,則返回值為0*/
int i=0;
LinkList p=L->next;
while(p)
{
i++;
if(compare(p->data,e)) // 找到這樣的數據元素
return i;
p=p->next;
}
return 0;
}
Status PriorElem(LinkList L,ElemType cur_e,ElemType &pre_e)
{ // 初始條件: 線性表L已存在
/* 操作結果: 若cur_e是L的數據元素,且不是第一個,則用pre_e返回它的前驅,
返回OK;否則操作失敗,pre_e無定義,返回INFEASIBLE*/
LinkList q,p=L->next; // p指向第一個結點
while(p->next) // p所指結點有後繼
{
q=p->next; // q為p的後繼
if(q->data==cur_e)
{
pre_e=p->data;
return OK;
}
p=q; // p向後移
}
return INFEASIBLE;
}
Status NextElem(LinkList L,ElemType cur_e,ElemType &next_e)
{ // 初始條件:線性表L已存在
/* 操作結果:若cur_e是L的數據元素,且不是最後一個,則用next_e返回它的後繼,
返回OK;否則操作失敗,next_e無定義,返回INFEASIBLE*/
LinkList p=L->next; // p指向第一個結點
while(p->next) // p所指結點有後繼
{
if(p->data==cur_e)
{
next_e=p->next->data;
return OK;
}
p=p->next;
}
return INFEASIBLE;
}
Status ListInsert(LinkList L,int i,ElemType e) // 算法2.9。不改變L
{ // 在帶頭結點的單鏈線性表L中第i個位置之前插入元素e
int j=0;
LinkList p=L,s;
while(p&&j<i-1) // 尋找第i-1個結點
{
p=p->next;
j++;
}
if(!p||j>i-1) // i小於1或者大於表長
return ERROR;
s=(LinkList)malloc(sizeof(LNode)); // 生成新結點
s->data=e; // 插入L中
s->next=p->next;
p->next=s;
return OK;
}
Status ListDelete(LinkList L,int i,ElemType &e) // 算法2.10。不改變L
{ // 在帶頭結點的單鏈線性表L中,刪除第i個元素,並由e返回其值
int j=0;
LinkList p=L,q;
while(p->next&&j<i-1) // 尋找第i個結點,並令p指向其前驅
{
p=p->next;
j++;
}
if(!p->next||j>i-1) // 刪除位置不合理
return ERROR;
q=p->next; // 刪除並釋放結點
p->next=q->next;
e=q->data;
free(q);
return OK;
}
void ListTraverse(LinkList L,void(*vi)(ElemType))
//vi的形參類型為ElemType,與bo2-1.cpp中相應函數的形參類型ElemType&不同
{ // 初始條件:線性表L已存在。操作結果:依次對L的每個數據元素調用函數vi()
LinkList p=L->next;
while(p)
{
vi(p->data);
p=p->next;
}
printf("\n");
}
1)存儲結構:
[cpp]
struct LNode
{
ElemType data;
LNode * next;
};
typedef LNode * LinkList ;
2)基本操作:
[cpp]
void InitList(LinkList &L)
{ // 操作結果:構造一個空的線性表L
L=(LinkList)malloc(sizeof(LNode)); // 產生頭結點,並使L指向此頭結點
if(!L) // 存儲分配失敗
exit(OVERFLOW);
L->next=NULL; // 指針域為空
}
void DestroyList(LinkList &L)
{ // 初始條件:線性表L已存在。操作結果:銷毀線性表L
LinkList q;
while(L)
{
q=L->next;
free(L);
L=q;
}
}
void ClearList(LinkList L) // 不改變L
{ // 初始條件:線性表L已存在。操作結果:將L重置為空表
LinkList p,q;
p=L->next; // p指向第一個結點
while(p) // 沒到表尾
{
q=p->next;
free(p);
p=q;
}
L->next=NULL; // 頭結點指針域為空
}
Status ListEmpty(LinkList L)
{ // 初始條件:線性表L已存在。操作結果:若L為空表,則返回TRUE,否則返回FALSE
if(L->next) // 非空
return FALSE;
else
return TRUE;
}
int ListLength(LinkList L)
{ // 初始條件:線性表L已存在。操作結果:返回L中數據元素個數
int i=0;
LinkList p=L->next; // p指向第一個結點
while(p) // 沒到表尾
{
i++;
p=p->next;
}
return i;
}
Status GetElem(LinkList L,int i,ElemType &e) // 算法2.8
{ // L為帶頭結點的單鏈表的頭指針。當第i個元素存在時,其值賦給e並返回OK,否則返回ERROR
int j=1; // j為計數器
LinkList p=L->next; // p指向第一個結點
while(p&&j<i) // 順指針向後查找,直到p指向第i個元素或p為空
{
p=p->next;
j++;
}
if(!p||j>i) // 第i個元素不存在
return ERROR;
e=p->data; // 取第i個元素
return OK;
}
int LocateElem(LinkList L,ElemType e,Status(*compare)(ElemType,ElemType))
{ // 初始條件: 線性表L已存在,compare()是數據元素判定函數(滿足為1,否則為0)
/*操作結果: 返回L中第1個與e滿足關系compare()的數據元素的位序。
若這樣的數據元素不存在,則返回值為0*/
int i=0;
LinkList p=L->next;
while(p)
{
i++;
if(compare(p->data,e)) // 找到這樣的數據元素
return i;
p=p->next;
}
return 0;
}
Status PriorElem(LinkList L,ElemType cur_e,ElemType &pre_e)
{ // 初始條件: 線性表L已存在
/* 操作結果: 若cur_e是L的數據元素,且不是第一個,則用pre_e返回它的前驅,
返回OK;否則操作失敗,pre_e無定義,返回INFEASIBLE*/
LinkList q,p=L->next; // p指向第一個結點
while(p->next) // p所指結點有後繼
{
q=p->next; // q為p的後繼
if(q->data==cur_e)
{
pre_e=p->data;
return OK;
}
p=q; // p向後移
}
return INFEASIBLE;
}
Status NextElem(LinkList L,ElemType cur_e,ElemType &next_e)
{ // 初始條件:線性表L已存在
/* 操作結果:若cur_e是L的數據元素,且不是最後一個,則用next_e返回它的後繼,
返回OK;否則操作失敗,next_e無定義,返回INFEASIBLE*/
LinkList p=L->next; // p指向第一個結點
while(p->next) // p所指結點有後繼
{
if(p->data==cur_e)
{
next_e=p->next->data;
return OK;
}
p=p->next;
}
return INFEASIBLE;
}
Status ListInsert(LinkList L,int i,ElemType e) // 算法2.9。不改變L
{ // 在帶頭結點的單鏈線性表L中第i個位置之前插入元素e
int j=0;
LinkList p=L,s;
while(p&&j<i-1) // 尋找第i-1個結點
{
p=p->next;
j++;
}
if(!p||j>i-1) // i小於1或者大於表長
return ERROR;
s=(LinkList)malloc(sizeof(LNode)); // 生成新結點
s->data=e; // 插入L中
s->next=p->next;
p->next=s;
return OK;
}
Status ListDelete(LinkList L,int i,ElemType &e) // 算法2.10。不改變L
{ // 在帶頭結點的單鏈線性表L中,刪除第i個元素,並由e返回其值
int j=0;
LinkList p=L,q;
while(p->next&&j<i-1) // 尋找第i個結點,並令p指向其前驅
{
p=p->next;
j++;
}
if(!p->next||j>i-1) // 刪除位置不合理
return ERROR;
q=p->next; // 刪除並釋放結點
p->next=q->next;
e=q->data;
free(q);
return OK;
}
void ListTraverse(LinkList L,void(*vi)(ElemType))
//vi的形參類型為ElemType,與bo2-1.cpp中相應函數的形參類型ElemType&不同
{ // 初始條件:線性表L已存在。操作結果:依次對L的每個數據元素調用函數vi()
LinkList p=L->next;
while(p)
{
vi(p->data);
p=p->next;
}
printf("\n");
}