一、算法描述
歸並排序算法完全遵循分治模式，將問題分解為若干子問題，如果子問題的規模足夠小，則直接求解，否則遞歸地求解各子問題。算法步驟如下所示：
1）將待排序的n個元素的序列分解為各具n/2個序列的兩個字序列
2）使用歸並排序遞歸地將兩個子序列排序
3）將兩個已排序的子序列合並，生成排好序的序列。
二、算法實現
1、遞歸版本
為了避免在合並兩個子序列時每次都要檢查是否某個子序列已全部處理完，在每個子序列最後都添加了一個“哨兵”元素。源碼如下所示：
[cpp]
#include <stdio.h>
#include <errno.h>
#ifndef INT_MAX
#define INT_MAX ((int)(~0U>>1))
#endif
#define ARRAY_SIZE(__s) (sizeof(__s) / sizeof(__s[0]))
static void merge(int *a, int start, int mid, int end)
{
int nl = mid - start + 1;
int nr = end - mid;
int sentinel = INT_MAX;
int left[nl + 1], right[nr + 1];
int i, j, k = start;
for (i = 0; i < nl; ++i) {
left[i] = a[k++];
}
/* Set sentinel */
left[i] = sentinel;
for (j = 0; j < nr; ++j) {
right[j] = a[k++];
}
/* Set sentinel */
right[j] = sentinel;
i = j = 0;
for (k = start; k <= end; ++k) {
if (left[i] <= right[j]) {
a[k] = left[i++];
} else {
a[k] = right[j++];
}
}
}
static void merge_sort(int *a, int start, int end)
{
int mid;
if ((start >= 0) && (start < end)) {
mid = (start + end) /2 ;
merge_sort(a, start, mid);
merge_sort(a, mid + 1, end);
merge(a, start, mid, end);
}
}
int main(void)
{
int source[] = { 7, 5, 2, 4, 6, 1, 5, 3};
int i;
printf("Before sort: ");
for (i = 0; i < ARRAY_SIZE(source); ++i) {
printf("%d ", source[i]);
}
printf("\n");
merge_sort(source, 0, ARRAY_SIZE(source) - 1);
printf("After sort: ");
for (i = 0; i < ARRAY_SIZE(source); ++i) {
printf("%d ", source[i]);
}
printf("\n");
return 0;
}
2、迭代版本
這個版本是在維基百科上看到的， 做一個簡單的分析，記錄一下，代碼如下所示：
[cpp]
#include <stdio.h>
#include <errno.h>
#define ARRAY_SIZE(__s) (sizeof(__s) / sizeof(__s[0]))
void merge_sort_iterate(int *source, int n)
{
int i, left_min, right_min, left_max, right_max, next;
int tmp[n];
for (i = 1; i < n; i *= 2) {
/*
* 將數組分段處理，每個段的長度為2*i。其中每段的前一半作為左半部，
* 後一半作為右半部，然後合並。
*/
for (left_min = 0; left_min < n - 1; left_min = right_max) {
/*
* left_max其實是左半部的長度，right_max其實是右半部的長度，
* 所以應該叫left_len、righ_len更合適一些。
*/
right_min = left_max = left_min + i;
right_max = left_max + i;
if (right_max > n) {
right_max = n;
}
next = 0;
/*
* 合並當前段中左半部和右半部的元素
*/
while ((left_min < left_max) &&
(right_min < right_max)) {
tmp[next++] = source[left_min] > source[right_min] ?
source[right_min++] : source[left_min++];
}
/*
* 左半部和右半部從長度為1開始處理，每次處理後，左半部和右半部
* 組成的段是排好序的，所以在下次處理中，每個段的左半部和右半部
* 已經是排好序的。如果判斷條件為真，說明右半部中當前元素已經全
* 部放在tmp中，而左半部中剩余的元素肯定比已經放在tmp中的元素大，
* 因此循環將左半部中剩余的元素放在段的後面。
*/
while (left_min < left_max) {
source[--right_min] = source[--left_max];
}
/*
* 將tmp中已經排好序的元素放回到原數組中，此時source數組中的元素不是
* 並不是已經排好序了，只是段中已經排好序。
*/
while (next > 0) {
source[--right_min] = tmp[--next];
}
}
}
}
int main(void)
{
int source[] = { 7, 5, 2, 4, 6, 1, 5, 3};
int i;
printf("Before sort: ");
for (i = 0; i < ARRAY_SIZE(source); ++i) {
printf("%d ", source[i]);
}
printf("\n");
merge_sort_iterate(source, ARRAY_SIZE(source));
printf("After sort: ");
for (i = 0; i < ARRAY_SIZE(source); ++i) {
printf("%d ", source[i]);
}
printf("\n");
return 0;
}
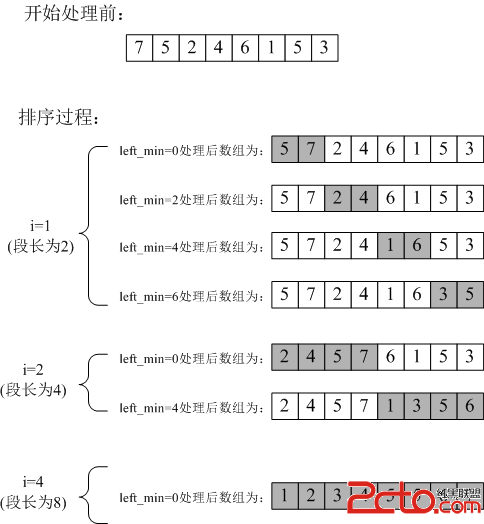
其處理過程如下圖所示（陰影部分為代碼注釋中提到的當前正在處理的段）：
3、時間復雜度O(1)版本
這個是在搜索的時候看到的一個題目，就是在合並兩個已經排好序的子序列後時，不分配臨時存儲左右子序列的空間，而是使用類似插入排序的方法，將右子序列的元素插入到左子序列中。雖然這種方法節省了空間，但是時間復雜度由nlg(n)變為(n^2)lgn，犧牲了性能。代碼實現如下：
[cpp]
#include <stdio.h>
#include <errno.h>
#ifndef INT_MAX
#define INT_MAX ((int)(~0U>>1))
#endif
#define ARRAY_SIZE(__s) (sizeof(__s) / sizeof(__s[0]))
static void merge(int *a, int start, int mid, int end)
{
int i, left, right;
int key;
for (right = mid + 1; right <= end; ++right) {
left = right - 1;
key = a[right];
while (a[left] > key) {
a[left + 1] = a[left];
--left;
}
a[left + 1] = key;
}
}
static void merge_sort(int *a, int start, int end)
{
int mid;
if ((start >= 0) && (start < end)) {
mid = (start + end) /2 ;
merge_sort(a, start, mid);
merge_sort(a, mid + 1, end);
merge(a, start, mid, end);
}
}
int main(void)
{
int source[] = { 7, 5, 2, 4, 6, 1, 5, 3};
int i;
printf("Before sort: ");
for (i = 0; i < ARRAY_SIZE(source); ++i) {
printf("%d ", source[i]);
}
printf("\n");
merge_sort(source, 0, ARRAY_SIZE(source) - 1);
printf("After sort: ");
for (i = 0; i < ARRAY_SIZE(source); ++i) {
printf("%d ", source[i]);
}
printf("\n");
return 0;
}
三、算法分析
當輸入的序列只有一個元素時，歸並排序需要常量時間。假設當有n個元素時，使用歸並排序算法來排序需要的時間為T(n)。當有n>1個元素時，按如下方式來分解時間：
1）分解，分解步驟僅僅是計算子數組的中間位置，需要常量時間，記作D(n)，D(n)=Θ(1)。
2）解決，遞歸地求解兩個規模均為n/2的子序列的排序問題，運行時間為2T(n/2)。
3）合並，將兩個規模為n/2的子序列合並到規模為n的序列中需要的的時間記作C(n)， C(n)=Θ(n)。
根據上面的的分析，可以得到歸並排序的運行時間公式，如下所示：
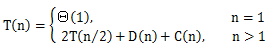D(n)和C(n)相加時，相當於是把一個Θ(1)函數與另一個Θ(n)函數相加，相加的和是n的一個線性函數，即Θ(n)。因此我們將T(n)的計算公式轉換為下面的形式：
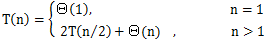為了更直觀地理解T(n)的遞歸式，以及後面分析這個運行時間的分解，繼續重寫T(n)遞歸式。假設c為求解規模為1的為所需的時間以及在分解步驟和合並步驟處理每個數組元素所需的時間，將T(n)的遞歸式重寫為下面的形式：
相同常量一般不可能剛好既代表求解規模為1的問題的運行時間，又代表在分解步驟和合並步驟處理每個數組元素的時間，但是這兩個時間肯定都是一個常量，為了後續的分析，做這樣的假設不會影響最終的結果。
為方便起見，假設n剛好是2的冪，將T(n)遞歸式用下面的樹來表示：
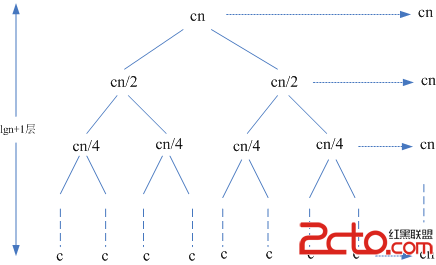
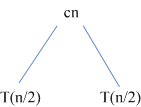樹中各個節點的值相加得到T(n)的值，其中cn為分解序列和合並序列所需的時間，T(n/2)為解決子序列排序問題所需的時間。將規模為n/2的子序列的問題進一步分解，得到下面的等價樹：
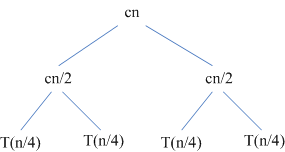在第二層的遞歸中，兩個子結點中每個引起的代價都是cn/2，但是此時子問題的規模還是沒有不夠小，也就是不能直接求解，所以還需要進一步的分解，直到問題規模下降到1，這時每個子問題的代價就很容易計算出來，其代價為c，如下圖所示：
下面具體分析下層數的計算和每層所需的代價的計算。
第一層只有一個節點，規模為n；第二層每個節點的規模為n/2，第三層每個節點的規模為n/4，以此類推直到節點的規模為1.假設k為層數，每層節點的規模為S(k)，則得到下面的計算公式：
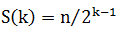問題的規模為1時，k的值為lgn+1，也就是上圖中分解得到的樹的層數。
現在需要確定分解和組合每層節點所需要的代價。總的問題規模為n，在分解問題時每層的節點的規模為n/2^(k-1)，其中k為層數，每層各節點的問題規模相加得到的總規模仍為n，因此每層的節點個數為2^(k-1)，將每個節點所需的代價乘以節點個數，即得到每層所需要的代碼，如下所示：
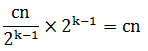為了計算T(n)遞歸式表示的總代價，只要把各層的代價加起來，遞歸樹有lgn+1層，每層的代價為均為cn，所以總的代價為cn(lgn+1)=cnlgn+cn。忽略低階項和常量c，得到時間復雜度為Θ(nlgn)。從上面的分析可以看出，歸並排序是一種穩定的排序算法，最壞、最好情況下時間復雜度均為Θ(nlgn)，平均時間復雜度也為Θ(nlgn)。
歸並排序的空間復雜度為Θ(n)。這個空間復雜度有些疑問，網上看到這樣的解釋“由於歸並排序在歸並過程中需要與原始記錄序列同樣數量的存儲空間存放歸並結果以及遞歸時深度為log2n的棧空間，因此空間復雜度為O(n+logn)”，但是感覺這個解釋說不通。我是這樣理解的，遞歸就是要高度抽象，在遞歸式中對左半部和右半部分別排序看作一個過程，真正要考慮的空間是在對左半部和右半部排序之後合並時需要的空間，因此空間復雜度為Θ(n)。這個理解很是牽強,,,,,
