題意：一棵蘋果樹有n個結點，開始時每個結點有一個蘋果，這n個結點由m條枝連起來，現執行以下兩種操作，C x：如果結點x原來有蘋果，則把它摘掉，如果沒有，則長出1個蘋果。Q x：詢問以x為根的樹的蘋果共幾個？
——>>這題轉換是關鍵！要求以x為根的樹的蘋果共幾個，如果能夠轉換為求一個數組a的[L, R]上的連續和，那就可以用ST或者BIT了。事實證明，確實可以做到這種轉換。
例如：原來的樹如下：如果詢問2，那麼共有2、4、5這3個蘋果，但2、4、5不是連續的呀？？？
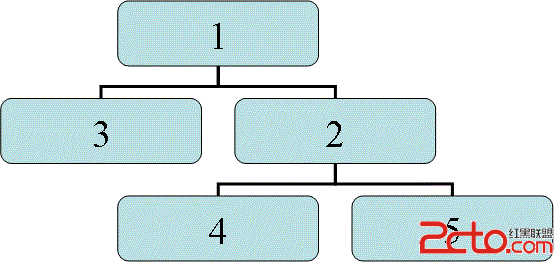得用dfs轉換後如下：[L, R]，其中所有的L存於L數組中，所有的R存於R數組中，R為新編號。
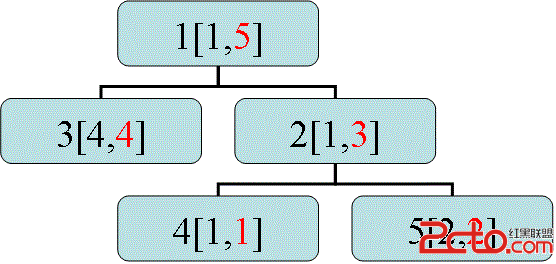如果詢問2，也就是求數組a在[1, 3]上的連續和。利用BIT或者ST就可解決TLE的問題啦。
（知道這樣做可以省時間，但也很容易TLE的，我用上ST，TLE了幾次，改用樹狀數組，TLE了十余次，最後，將那個vector<int>G[maxn]改為typedefvector<int> INT;
vector<INT>G(maxn);竟然奇跡般地AC!了什麼情況，這是……）
[cpp]
#include <iostream>
#include <cstdio>
#include <vector>
#include <cstring>
using namespace std;
const int maxn = 100000 + 10; //N ≤ 100,000,M ≤ 100,000
int lowerbit[maxn], C[maxn], L[maxn], R[maxn], dfs_clock = 1, N;
bool vis[maxn], a[maxn];
typedef vector<int> INT;
vector<INT> G(maxn);
void dfs(int x) //對蘋果樹進行重新編號
{
vis[x] = 1; //標記為已訪問
L[x] = dfs_clock; //dfs_clock為計數器
for(unsigned int i = 0; i < G[x].size(); i++) //對所有相鄰結點進行檢查
{
int v = G[x][i];
if(!vis[v]) dfs(v); //如果沒訪問過，訪問
}
R[x] = dfs_clock++; //新編號在這裡！
}
void update(int x) //BIT更新函數
{
int val;
if(a[x]) val = -1;
else val = 1;
a[x] = !a[x]; //該結點取反即可
while(x <= N)
{
C[x] += val;
x += lowerbit[x];
}
}
int sum(int x) //BIT求數組a的前x項和
{
int ret = 0;
while(x > 0)
{
ret += C[x];
x -= lowerbit[x];
}
return ret;
}
int main()
{
int M, i, u, v;
scanf("%d", &N);
for(i = 1; i <= N; i++) //初始化
{
C[i] = i&(-i); //C為BIT結點的連續和
a[i] = true;
lowerbit[i] = i&(-i); //lowerbit為二進制表達式中最右邊的1所對應的值,這裡，用i&(-i)比用C[i]直接賦值要快！
}
for(i = 0; i < N-1; i++)
{
scanf("%d%d", &u, &v);
G[u].push_back(v); //測試證明，不需要考慮雙向
}
dfs(1);
scanf("%d", &M);
char ch;
for(i = 0; i < M; i++)
{
getchar();
scanf("%c%d", &ch, &v);
if(ch == 'Q') printf("%d\n", sum(R[v])-sum(L[v]-1)); //經測試，先判斷為'Q'用的時間更少
else update(R[v]);
}
return 0;
}
