拉格朗日插值法
(*以下定義選自維基百科)
 算法流程圖
算法流程圖
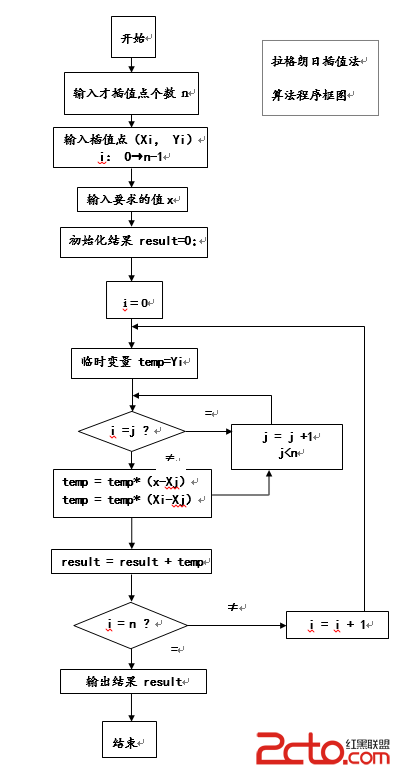 算法代碼
[cpp]
#include<iostream>
#include<string>
#include<vector>
using namespace std;
double Lagrange(int N,vector<double>&X,vector<double>&Y,double x);
int main(){
char a='n';
do{
cout<<"請輸入差值次數n的值:"<<endl;
int N;
cin>>N;
vector<double>X(N,0);
vector<double>Y(N,0);
cout<<"請輸入插值點對應的值及函數值(Xi,Yi):"<<endl;
for(int a=0;a<N;a++){
cin>>X[a]>>Y[a];
}
cout<<"請輸入要求值x的值:"<<endl;
double x;
cin>>x;
double result=Lagrange(N,X,Y,x);
cout<<"由拉格朗日插值法得出結果: "<<result<<endl;
cout<<"是否要繼續?(y/n):";
cin>>a;
}while(a=='y');
return 0;
}
double Lagrange(int N,vector<double>&X,vector<double>&Y,double x){
double result=0;
for(int i=0;i<N;i++){
double temp=Y[i];
for(int j=0;j<N;j++){
if(i!=j){
temp = temp*(x-X[j]);
temp = temp/(X[i]-X[j]);
}
}
result += temp;
}
return result;
};
牛頓插值法
牛頓插值法公式如下,具體參見(百度文檔)
算法代碼
[cpp]
#include<iostream>
#include<string>
#include<vector>
using namespace std;
double Lagrange(int N,vector<double>&X,vector<double>&Y,double x);
int main(){
char a='n';
do{
cout<<"請輸入差值次數n的值:"<<endl;
int N;
cin>>N;
vector<double>X(N,0);
vector<double>Y(N,0);
cout<<"請輸入插值點對應的值及函數值(Xi,Yi):"<<endl;
for(int a=0;a<N;a++){
cin>>X[a]>>Y[a];
}
cout<<"請輸入要求值x的值:"<<endl;
double x;
cin>>x;
double result=Lagrange(N,X,Y,x);
cout<<"由拉格朗日插值法得出結果: "<<result<<endl;
cout<<"是否要繼續?(y/n):";
cin>>a;
}while(a=='y');
return 0;
}
double Lagrange(int N,vector<double>&X,vector<double>&Y,double x){
double result=0;
for(int i=0;i<N;i++){
double temp=Y[i];
for(int j=0;j<N;j++){
if(i!=j){
temp = temp*(x-X[j]);
temp = temp/(X[i]-X[j]);
}
}
result += temp;
}
return result;
};
牛頓插值法
牛頓插值法公式如下,具體參見(百度文檔)
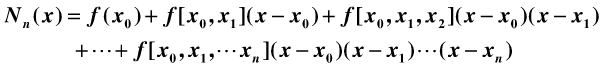 算法流程
算法流程
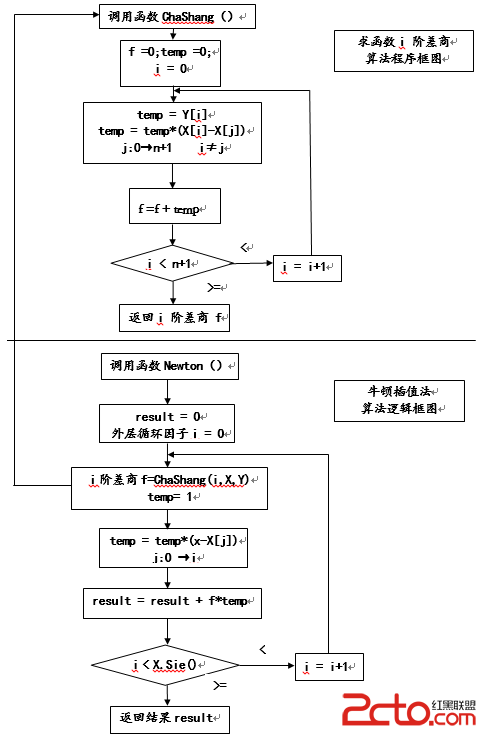 算法代碼
[cpp]
#include<iostream>
#include<string>
#include<vector>
using namespace std;
double ChaShang(int n,vector<double>&X,vector<double>&Y);
double Newton(double x,vector<double>&X,vector<double>&Y);
int main(){
int n;
cin>>n;
vector<double>X(n,0);
vector<double>Y(n,0);
for(int i=0;i<n;i++){
cin>>X[i]>>Y[i];
}
double x;
cin>>x;
cout<<Newton(x,X,Y);
}
double ChaShang(int n,vector<double>&X,vector<double>&Y){
double f=0;
double temp=0;
for(int i=0;i<n+1;i++){
temp=Y[i];
for(int j=0;j<n+1;j++)
if(i!=j) temp /= (X[i]-X[j]);
f += temp;
}
return f;
}
double Newton(double x,vector<double>&X,vector<double> &Y){
double result=0;
for(int i=0;i<X.size();i++){
double temp=1;
double f=ChaShang(i,X,Y);
for(int j=0;j<i;j++){
temp = temp*(x-X[j]);
}
result += f*temp;
}
return result;
}
實驗過程原始記錄
給定函數四個點的數據如下:
算法代碼
[cpp]
#include<iostream>
#include<string>
#include<vector>
using namespace std;
double ChaShang(int n,vector<double>&X,vector<double>&Y);
double Newton(double x,vector<double>&X,vector<double>&Y);
int main(){
int n;
cin>>n;
vector<double>X(n,0);
vector<double>Y(n,0);
for(int i=0;i<n;i++){
cin>>X[i]>>Y[i];
}
double x;
cin>>x;
cout<<Newton(x,X,Y);
}
double ChaShang(int n,vector<double>&X,vector<double>&Y){
double f=0;
double temp=0;
for(int i=0;i<n+1;i++){
temp=Y[i];
for(int j=0;j<n+1;j++)
if(i!=j) temp /= (X[i]-X[j]);
f += temp;
}
return f;
}
double Newton(double x,vector<double>&X,vector<double> &Y){
double result=0;
for(int i=0;i<X.size();i++){
double temp=1;
double f=ChaShang(i,X,Y);
for(int j=0;j<i;j++){
temp = temp*(x-X[j]);
}
result += f*temp;
}
return result;
}
實驗過程原始記錄
給定函數四個點的數據如下:
 試用拉格朗日插值確定函數在x=2.101,4.234處的函數值。
運行得到結果:
試用拉格朗日插值確定函數在x=2.101,4.234處的函數值。
運行得到結果:
 已知用牛頓插值公式求的近似值。
運行程序得到結果: 2.26667
實驗分析
1、Lagrange插值法和Newton插值法解決實際問題中關於只提供復雜的離散數據的函數求值問題,通過將所考察的函數簡單化,構造關於離散數據實際函數f(x)的近似函數P(x),從而可以計算未知點出的函數值,是插值法的基本思路。
2、實際上Lagrange插值法和Newton插值法是同一種方法的兩種變形,其構造擬合函數的思路是相同的,而實驗中兩個實際問題用兩種算法計算出結果是相同的。
3、實驗所得結果精確度並不高,一方面是因為所給數據較少,另一方面也是主要方面在Win32中C++中數據類型double精度只有7位,計算機在進行浮點運算時截斷運算會導致誤差。實際問題中,測量數據也可能導致誤差。
4、在解決實際問題中,更多是利用精確且高效的計算機求解。所以解決問題時不僅要構造可求解的算法,更重要是構造合理的可以編寫成程序由計算機求解的算法,而算法的優化不僅可以節省時間空間,更能得到更為精確有價值的結果。
已知用牛頓插值公式求的近似值。
運行程序得到結果: 2.26667
實驗分析
1、Lagrange插值法和Newton插值法解決實際問題中關於只提供復雜的離散數據的函數求值問題,通過將所考察的函數簡單化,構造關於離散數據實際函數f(x)的近似函數P(x),從而可以計算未知點出的函數值,是插值法的基本思路。
2、實際上Lagrange插值法和Newton插值法是同一種方法的兩種變形,其構造擬合函數的思路是相同的,而實驗中兩個實際問題用兩種算法計算出結果是相同的。
3、實驗所得結果精確度並不高,一方面是因為所給數據較少,另一方面也是主要方面在Win32中C++中數據類型double精度只有7位,計算機在進行浮點運算時截斷運算會導致誤差。實際問題中,測量數據也可能導致誤差。
4、在解決實際問題中,更多是利用精確且高效的計算機求解。所以解決問題時不僅要構造可求解的算法,更重要是構造合理的可以編寫成程序由計算機求解的算法,而算法的優化不僅可以節省時間空間,更能得到更為精確有價值的結果。