復化梯形
將積分區間[a,b]劃分n等分，步長，求積節點，在每個小區間上應用梯形公式
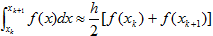然後將它們累加求和，作為所求積分I的近似值.
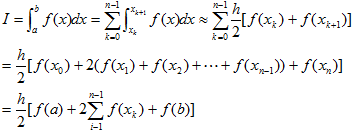記
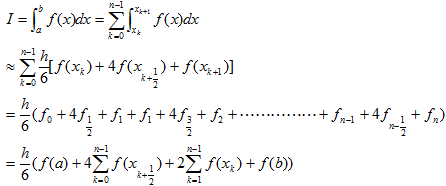式為復化梯形求積公式，下標n表示將區間n等分。
算法流程
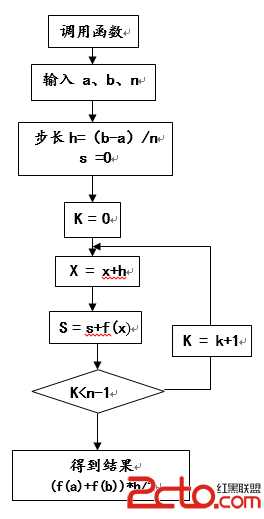算法代碼
[cpp]
double f(double x){
if(x==0) return 1;
else return (sin(x)/x);
}
double FuhuaTixing(int n,double a,double b){
double h = (b-a)/n;
double x = a;
double s = 0;
for(int k=0; k< n-1; k++){
x += h;
s += f(x);
}
double T = (f(a)+s*2+f(b))*h/2;
return T;
}
int main(){
char ans='n';
do{
cout<<"請輸入積分區間(a,b)："<<endl;
double a;
double b;
cin>>a>>b;
cout<<"請輸入等分份數n： "<<endl;
int n; cin>>n;
cout<<"由復化梯形公式球的結果："<<FuhuaTixing(n,a,b)<<endl;
cout<<"是否要繼續？(y/n)";
cin>>ans;
}while(ans == 'y');
return 0;
}
復化辛復生
將積分區間[a,b]劃分n等分，記子區間的中點為在每個小區間上應用辛普森公式，則有
其中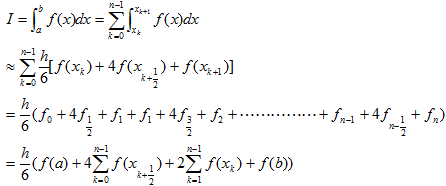
記
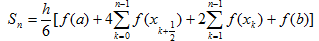式為復化辛普森求積公式。
算法流程
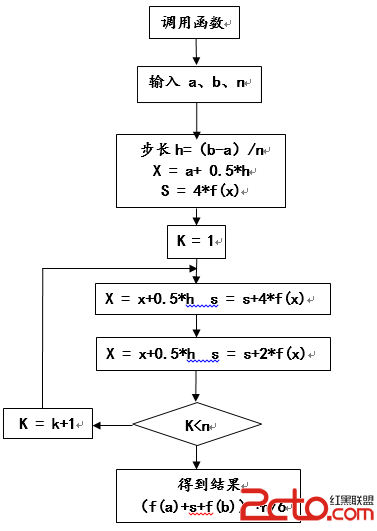算法代碼
[cpp]
double f(double x){
if (x==0)
return 1;
else return (sin(x)/x);
}
double Xinfusheng(double a,double b,int n){
double h = (b-a)/n;
double x = a+1/2*h;
double s = 4*f(x);
for(int k=1;k<n;k++){
x += 1/2*h;
s += 4*f(x);
x += 1/2*h;
s += 2*f(x);
}
double T=(f(a)+s+f(b))*h/6;
return T;
}
int main(){
char ans='n';
do{
cout<<"請輸入積分區間(a,b)："<<endl;
double a;
double b;
cin>>a>>b;
cout<<"請輸入等分份數n： "<<endl;
int n;
cin>>n;
cout<<"由復化梯形公式球的結果："<<Xinfusheng(a,b,n)<<endl;
cout<<"是否要繼續？(y/n)";
cin>>ans;
}while(ans == 'y');
return 0;
}
實驗過程原始記錄
分別用復化梯形公式和復化辛浦生公式計算定積分
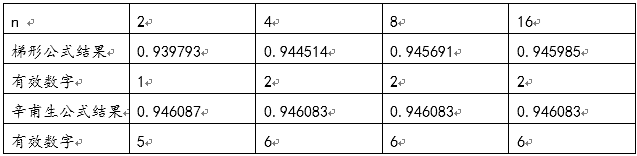
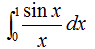取n=2，4，8，16，精確解為0.9460831
實驗結果及分析
1、用復化梯形公式和復化辛甫生公式都能得到較為准確的結果，且等分份數越多，結果的精度越高，梯形公式雖然在等分16份時得到精度與等分4份時相同，但已經越來越接近精確解。辛甫生公式由於C++運算中雙精度數值（double）只有7位有效數字的限制，增加等分份數時不容易看出其精度的增加。
2、比較兩種方法運算的結果，復化辛甫生公式等分2份時實際要計算5個點的函數值，與復化梯形公式等分4份時計算量基本相同，但得到精度明顯復化辛甫生公式要精確很多。
3、復化梯形公式和復化辛甫生公式對於光滑性較差的被積函數都能得到較為精確的結果，而且公式簡單，十分利於編譯簡單的程序由計算機運算，因而得到廣泛的應用。
4、實驗中的主要誤差來自於計算機浮點運算中的截余。
