題目：給定一個多邊形A，問能否穿過多邊形的洞B。
分析：計算幾何、凸包、旋轉卡殼、點與多邊形關系。問題實際是在求多邊形A的最小寬度和多邊形B能容納的最常線段長度。
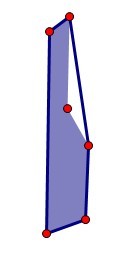1.對於多邊形A，構造凸包利用，旋轉卡殼求出對踵點對，然後求出最小的高。
2. 對於多邊形B，所求的最長線段，一定經過多邊形上的至少兩個點，枚舉所有點對，計算被截取的最長部分即可。
[cpp]
#include <algorithm>
#include <iostream>
#include <cstdlib>
#include <cstdio>
#include <cmath>
using namespace std;
typedef struct pnode
{
double x,y,d;
pnode( double a, double b ) {x = a;y = b;}
pnode(){};
}point;
point H[ 21 ];
point C[ 21 ];
point P0,Pn;
typedef struct lnode
{
double x,y,dx,dy,d;
int id,hit,sign;
lnode( point a, point b ) {x = a.x;y = a.y;dx = b.x-a.x;dy = b.y-a.y;}
lnode(){};
}line;
//兩點間距離
double dist( point a, point b )
{
return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}
//點到直線距離
double dist( point a, line l )
{
return fabs(l.dx*(a.y-l.y)-l.dy*(a.x-l.x))/sqrt(l.dx*l.dx+l.dy*l.dy);
}
//叉乘 ab*ac
double crossproduct( point a, point b, point c )
{
return (b.x-a.x)*(c.y-a.y)-(c.x-a.x)*(b.y-a.y);
}
//坐標排序
bool cmp1( point a, point b )
{
if ( a.x == b.x ) return a.y < b.y;
else return a.x < b.x;
}
//級角排序
bool cmp2( point a, point b )
{
double cp = crossproduct( P0, a, b );
if ( cp == 0 ) return a.d < b.d;
else return cp > 0;
}
//凸包掃描算法
double Graham( int N )
{
sort( C+0, C+N, cmp1 );
P0 = C[0];
for ( int i = 1 ; i < N ; ++ i )
C[i].d = dist( P0, C[i] );
sort( C+1, C+N, cmp2 );
//計算凸包
int top = 2;
for ( int i = 3 ; i < N ; ++ i ) {
while ( top > 0 && crossproduct( C[top-1], C[top], C[i] ) <= 0 ) -- top;
C[++ top] = C[i];
}
C[++ top] = C[0];
//旋轉卡殼，求對踵點對
int L = 0,R = 1;
double D = 500.000;
do{
while ( crossproduct( C[R], C[L], C[(L+1)%top] ) <= crossproduct( C[(R+1)%top], C[L], C[(L+1)%top] ) )
R = (R+1)%top;
D = min( D, dist( C[R], line( C[L], C[(L+1)%top] ) ) );
L = (L+1)%top;
}while ( L );
return D;
}
//直線與線段相交判斷
bool l_cross_s( line b, line a )
{
double t1 = b.dx*(a.y-b.y)-b.dy*(a.x-b.x);
double t2 = b.dx*(a.y+a.dy-b.y)-b.dy*(a.x+a.dx-b.x);
return t1*t2 < 0;
}
//線段相交
bool s_cross_s( line a, line b )
{
double t1 = 0.0+a.dx*(b.y-a.y)-a.dy*(b.x-a.x);
double t2 = 0.0+a.dx*(b.y+b.dy-a.y)-a.dy*(b.x+b.dx-a.x);
double t3 = 0.0+b.dx*(a.y-b.y)-b.dy*(a.x-b.x);
double t4 = 0.0+b.dx*(a.y+a.dy-b.y)-b.dy*(a.x+a.dx-b.x);
return (t1*t2 < 0)&&(t3*t4 < 0);
}
//點在線段上
bool on( point p, line l )
{
if ( l.dx*(p.y-l.y)-l.dy*(p.x-l.x) == 0 )
if ( (p.x-l.x)*(p.x-l.x-l.dx) <= 0 )
if ( (p.y-l.y)*(p.y-l.y-l.dy) <= 0 )
return true;
return false;
}
//點在多邊形內
bool in( point p, point* P, int n )
{
double d[4][2] = {-101,-103,-103,101,101,-103,101,103};
for ( int t = 0 ; t < 4 ; ++ t ) {
line s1 = line( p, point( d[t][0], d[t][1] ) );
int count = 0;
for ( int i = 0 ; i < n ; ++ i ) {
line s2 = line( P[i], P[i+1] );
if ( on( p, s2 ) ) return true;
if ( s_cross_s( s1, s2 ) ) count ++;
if ( on( P[i], s1 ) && l_cross_s( s1, line( P[i+1], P[(i-1+n)%n] ) ) ) count ++;
}
if ( count%2 == 0 ) return false;
}
return true;
}
//兩直線交點
point crosspoint( line l, line m )
{
point a = point( m.x, m.y );
point b = point( m.x+m.dx, m.y+m.dy );
if ( m.dx*l.dy == m.dy*l.dx ) {
if ( dist( point( l.x, l.y ), a ) < dist( point( l.x, l.y ), b ) )
return a;
else return b;
}else {
double a1 = -l.dy,b1 = l.dx,c1 = l.dx*l.y-l.dy*l.x;
double a2 = -m.dy,b2 = m.dx,c2 = m.dx*m.y-m.dy*m.x;
double x = (c1*b2-c2*b1)/(a1*b2-a2*b1);
double y = (c1*a2-c2*a1)/(b1*a2-b2*a1);
return point( x, y );
}
}
//計算空的最大長度
double Calcul( int N )
{
H[N] = H[0];
point X[ 21 ];
double D = 0.0;
for ( int i = 0 ; i < N ; ++ i )
for ( int j = i+1 ; j < N ; ++ j ) {
line l = line( H[i], H[j] );
int S = 0;
for ( int k = 0 ; k < N ; ++ k ) {
line m = line( H[k], H[k+1] );
if ( l_cross_s( l, m ) )
X[S ++] = crosspoint( l, m );
}
X[S ++] = H[i];
X[S ++] = H[j];
P0 = point( -101, -103 );
for ( int k = 0 ; k < S ; ++ k )
X[k].d = dist( P0, X[k] );
sort( X, X+S, cmp2 );
double sum = 0.0;
int fla = 0;
for ( int i = 1 ; i < S ; ++ i ) {
if ( in( point( (X[i-1].x+X[i].x)/2, (X[i-1].y+X[i].y)/2 ), H, N ) ) {
if ( fla ) sum += dist( X[i-1], X[i] );
else sum = dist( X[i-1], X[i] );
D = max( D, sum );
fla = 1;
}
}
}
return D;
}
int main()
{
int T,N,M;
while ( scanf("%d",&T) != EOF )
while ( T -- ) {
scanf("%d",&N);
for ( int i = 0 ; i < N ; ++ i )
scanf("%lf%lf",&H[i].x,&H[i].y);
scanf("%d",&M);
for ( int i = 0 ; i < M ; ++ i )
scanf("%lf%lf",&C[i].x,&C[i].y);
//計算硬幣最小寬度
double d = Graham( M );
//計算空的最大長度
double D = Calcul( N );
if ( d <= D ) printf("legal\n");
else printf("illegal\n");
}
return 0;
}
