1、問題描述：
給定N個頂點的多邊形，每個頂點標有一個整數，每條邊上標有+(加)或是×(乘)號，並且N條邊按照順時針
依次編號為1~N。下圖給出了一個N＝4個頂點的多邊形。
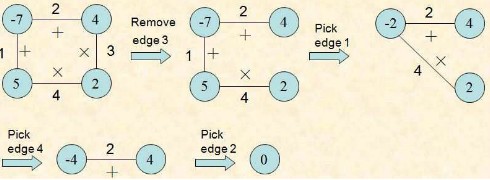
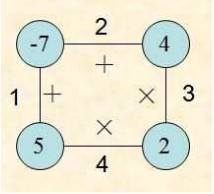游戲規則 ：(1) 首先，移走一條邊。 (2) 然後進行下面的操作： 選中一條邊E，該邊有兩個相鄰的頂點，不妨稱為V1和V2。對V1和V2頂點所標的整數按照E上所標運算符號(+或是×)進行運算，得到一個整數；用該整數標注一個新頂點，該頂點代替V1和V2 。 持續進行此操作，直到最後沒有邊存在，即只剩下一個頂點。該頂點的整數稱為此次游戲的得分(Score)。
2、問題分析：
解決該問題可用動態規劃中的最優子結構性質來解。
設所給的多邊形的頂點和邊的順時針序列為op[1],v[1],op[2],v[2],op[3],…,op[n],v[n] 其中，op[i]表示第i條邊所對應的運算符，v[i]表示第i個頂點上的數值，i=1~n。
在所給的多邊形中，從頂點i（1<=i<=n）開始，長度為j（鏈中有j個頂點）的順時針鏈p(i,j）可表示為v[i],op[i+1],…,v[i+j-1]，如果這條鏈的最後一次合並運算在op[i+s]處發生（1<=s<=j-1），則可在op[i+s]處將鏈分割為兩個子鏈p(i,s)和p(i+s,j-s)。www.2cto.com
設m[i,j,0]是鏈p(i,j)合並的最小值，而m[i,j,1]是最大值。若最優合並在op[i+s]處將p(i,j)分為兩個長度小於j的子鏈的最大值和最小值均已計算出。即：
a=m[i,s,0] b=m[i,s,1] c=m[i,s,0] d=m[i,s,1]
(1) 當op[i+s]=’+’時
m[i,j,0]=a+c ；m[i,j,1]=b+d
(2) 當op[i+s]=’*’時 www.2cto.com
m[i,j,0]=min{ac,ad,bc,bd} ； m[i,j,1]=max{ac,ad,bc,bd}
由於最優斷開位置s有1<=s<=j-1的j-1中情況。 初始邊界值為 m[i,1,0]=v[i] 1<=i<=n m[i,1,1]=v[i] 1<=i<=n
因為多變形式封閉的，在上面的計算中，當i+s>n時，頂點i+s實際編號為(i+s)modn。按上述遞推式計算出的m[i,n,1]記為游戲首次刪除第i條邊後得到的最大得分。
算法具體代碼如下：
[cpp]
//3d6 多邊形游戲
#include "stdafx.h"
#include <iostream>
using namespace std;
#define NMAX 100
int N,m[NMAX+1][NMAX+1][2],v[NMAX+1];
char op[NMAX+1];
void MinMax(int n,int i,int s,int j,int &minf,int &maxf);
int PloyMax(int n,int& p);
int main()
{
int p;
cout<<"請輸入多邊形頂點數："<<endl;
cin>>N;
for(int i=1; i<=N; i++)
{
cout<<"請輸入多邊形頂點"<<i<<"數值:"<<endl;
cin>>v[i];
m[i][1][0]=v[i];
m[i][1][1]=v[i];
cout<<"請輸入多邊形邊"<<i<<"運算符:"<<endl;
cin>>op[i];
}
cout<<"多邊形游戲首次刪除第"<<p<<"條邊，結果為："<<PloyMax(N,p)<<endl;
return 0;
}
void MinMax(int n,int i,int s,int j,int &minf,int &maxf)
{
int e[5];
int a=m[i][s][0],b=m[i][s][1];
int r=(i+s-1)%n+1;//多邊形的實際頂點編號
int c=m[r][j-s][0],d=m[r][j-s][1];
if(op[r-1]=='+')
{
minf=a+c;
maxf=b+d;
}
else
{
e[1]=a*c;
e[2]=a*d;
e[3]=b*c;
e[4]=d*b;
minf=e[1];
maxf=e[1];
for(int r=2;r<N;r++)
{
if(minf>e[r])minf=e[r];
if(maxf<e[r])maxf=e[r];
}
}
}
int PloyMax(int n,int& p)
{
int minf,maxf;
for(int j=2;j<=n;j++) //迭代鏈的長度
{
for(int i=1;i<=n;i++)//迭代首次刪掉第i條邊
{
for(int s=1 ;s<j;s++) //迭代斷開位置
{
MinMax(n,i,s,j,minf,maxf);
if(m[i][j][0]>minf) m[i][j][0]=minf;
if(m[i][j][1]<maxf) m[i][j][1]=maxf;
}
}
}
int temp=m[1][n][1];
p=1;
for(int i=2 ;i<=n; i++)
{
if(temp<m[i][n][1])
{
temp=m[i][n][1];
p=i;
}
}
return temp;
}
程序運行結果如下：
