題目意思：在一個n*m個方格中（頂點有（n+1）*(m+1)個），求所有三角形數，即三點不共線的所有情況。
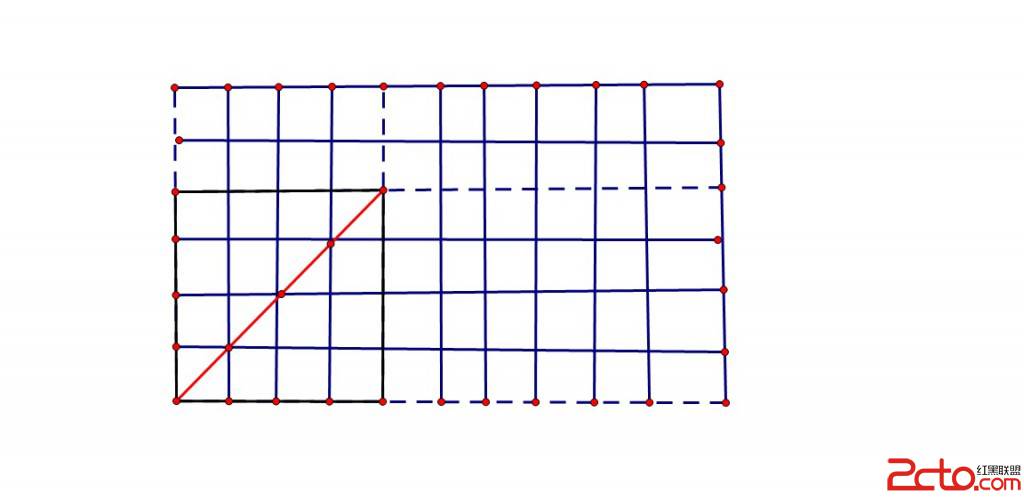
題解：令所有點的個數為t,用c[t,3]來枚舉所有情況，用總數扣去所有三點共線數就是所求的三角形數。那麼在求三點共線的情況時，水平和垂直的情況讀者自己考慮。對於傾斜的情況，先枚舉兩端的端點，如圖，在一個6*10的方格中選4*4的兩個端點，其中可構成三點花線的另一點的個數為最大公約數gcd(4,4) -1.如圖中的三個點，然後用乘於剩下的倍數（6-4+1）*（10-4+1），再乘於2（傾斜時有右上，右下兩種情況）.然後依次枚舉所有的矩形，求出所有三點共線的情況。於是所有情況減三點共線情況就是答案了。
代碼如下：
[cpp]
/*
* File: main.cpp
* Author: ssslpk
*
* Created on September 29, 2012, 12:20 PM
*/
#include <cstdlib>
#include<math.h>
#include<stdio.h>
#define int64 long long int
using namespace std;
#define N 1002
int64 f[N][N];
int gcd(int a,int b){return b? gcd(b,a%b): a;}
void init()
{
for(int i=1;i<=1000;i++)
{
for(int j=i;j<=1000;j++)
{
int d=gcd(i,j);
f[i][j]=f[j][i]=(int64)(d-1);
}
}
}
int main() {
int64 n,m;
init();
while(scanf("%lld%lld",&n,&m)!=EOF)
{
int64 sum=0;
for(int64 i=1;i<=n;i++)
{ www.2cto.com
for(int64 j=1;j<=m;j++)
{
sum+=f[j][i]*2*(n-i+1)*(m-j+1);
}
}
if(n>=2)sum+=(n+1)*(n)*(n-1)/6*(m+1);
if(m>=2)sum+=(m+1)*(m)*(m-1)/6*(n+1);
int64 t=(n+1)*(m+1);
int64 num;
if(t%3==0)
{
if((t-1)%2==0)num=t/3*(t-1)/2*(t-2);
else num=t/3*(t-2)/2*(t-1);
}
else if((t-1)%3==0)
{
if(t%2==0)
num=t/2*(t-1)/3*(t-2);
else num=(t-1)/6*(t-2)*t;
}
else
{
if((t-1)%2==0)
num=(t-1)/2*(t-2)/3*t;
else num=(t)/2*(t-2)/3*(t-1);
}
// printf("sum: %lld\n",sum);
printf("%lld\n",num-sum);
}
return 0;
}
