大家都知道，遞歸的本質和棧數據的存取很相似了，都是先進去，但是往往最後處理！再者對於遞歸函數的局部變量的存儲是按照棧的方式去存的，對於每一層的遞歸函數在棧中都保存了本層函數的局部變量，一邊該層遞歸函數結束時能夠保存原來該層的數據！如圖:
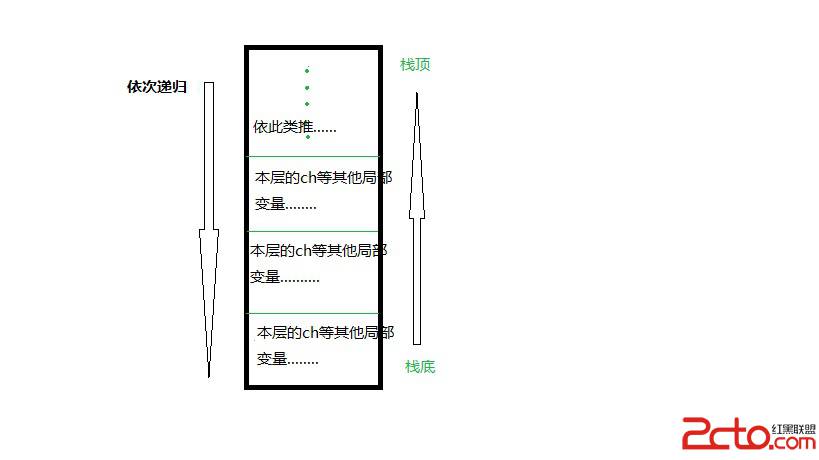如上圖遞歸式依次往下進行的，並且在該層遞歸函數還沒結束即將進入下一層遞歸調用時，將會把該層函數中的局部變量保存起來，以供下次使用!
好了，以上是遞歸函數的數據存儲方式，可是有時候我們又得抓頭了，遞歸的話，有時候又很難理解，貌似總也想不通!
於是我又把每一層遞歸函數化分為三部分了，第一部分:是遞歸調用前的一些數據處理，判斷以及遞歸結束判斷（當然了結束條件肯定在遞歸調用前，要不每次遞歸就不會結束了),第二部分:就是遞歸函數本身了。而第三部分:當然就是遞歸函數的後續處理代碼了！在這裡我想我們得想明白一件事情了，每一層的函數都是在上一層遞歸函數結束時才返回的然後接著處理該層遞歸函數剩下的部分!例如如下代碼:
[cpp]
#include<iostream>
#include<string>
using namespace std;
int i=0,j;
void reverse(string &s);
int main()
{
string s;
cin>>s;
j=i=s.size();
reverse(s);
cout<<s<<endl;
return 0;
}
void reverse(string &s)
{
char ch; //..........第一部分 ..........
i--;
ch=s[i];
cout<<ch<<endl; //這裡i是全局變量，而ch是局部變量會保存在棧中
if(-1==i)
return;
reverse(s); //本身的遞歸看做第二部分
//後續部分看做第三部分
s[--j]=ch; //這句當且僅當該遞歸函數中的reverse返回時 才執行
cout<<ch<<endl;
}
在以上代碼中，每一層只有當reverse（）結束了才會接著處理下面的s[--j]=ch;代碼，因為每一次遞歸進去的時候reverse()上面的代碼都已經處理了，所以當遞歸返回時處理的自然就是reverse()下面的代碼了，如此循環直到結束!不過我覺著最重要的還有一樣就是有時候不必刻意去關注的那麼細，也要有全局觀，例如我們只需要知道函數reverse()是繼續處理同樣的功能，沒必要再去想這個函數裡面又是怎麼樣怎麼樣的，我感覺肯定會抓狂的！希望跟我一樣糾結的朋友不在糾結遞歸了.........
另外，
遞歸的使用條件：
存在一個遞歸調用的終止條件；
每次遞歸的調用必須越來越靠近這個條件；只有這樣遞歸才會終止，否則是不能使用遞歸的！
總之，在你使用遞歸來處理問題之前必須首先考慮使用遞歸帶來的好處是否能補償
他所帶來的代價！否則，使用迭代算法會比遞歸算法要高效。
遞歸的基本原理：
１ 每一次函數調用都會有一次返回．當程序流執行到某一級遞歸的結尾處時，它會轉移到前一級遞歸繼續執行．
２ 遞歸函數中，位於遞歸調用前的語句和各級被調函數具有相同的順序．如打印語句 #1 位於遞歸調用語句前，它按照遞歸調用的順序被執行了 4 次．
３ 每一級的函數調用都有自己的局部變量．
４ 遞歸函數中，位於遞歸調用語句後的語句的執行順序和各個被調用函數的順序相反．
即位於遞歸函數入口前的語句，右外往裡執行；位於遞歸函數入口後面的語句，由裡往外執行。
５ 雖然每一級遞歸有自己的變量，但是函數代碼並不會得到復制．
６ 遞歸函數中必須包含可以終止遞歸調用的語句．
一旦你理解了遞歸(理解遞歸,關鍵是腦中有一幅代碼的圖片,函數執行到遞歸函數入口時,就擴充一段完全一樣的代碼,執行完擴充的代碼並return後,繼續執行前一次遞歸函數中遞歸函數入口後面的代碼),閱讀遞歸函數最容易的方法不是糾纏於它的執行過程，而是相信遞歸函數會順利完成它的任務。如果你的每個步驟正確無誤，你的限制條件設置正確，並且每次調用之後更接近限制條件，遞歸函數總是能正確的完成任務。
不算遞歸調用語句本身，到目前為止所執行的語句只是除法運算以及對quotient的值進行測試。由於遞歸調用這些語句重復執行，所以它的效果類似循環：當quotient的值非零時，把它的值作為初始值重新開始循環。但是，遞歸調用將會保存一些信息（這點與循環不同），也就好是保存在堆棧中的變量值。這些信息很快就會變得非常重要。
斐波那契數是典型的遞歸案例：
Fib(0) = 0 [基本情況] Fib(1) = 1 [基本情況]
對所有n > 1的整數：Fib(n) = (Fib(n-1) + Fib(n-2)) [遞歸定義]
遞歸算法一般用於解決三類問題：
(1)數據的定義是按遞歸定義的。(Fibonacci函數)
(2)問題解法按遞歸算法實現。(回溯)
(3)數據的結構形式是按遞歸定義的。(樹的遍歷，圖的搜索)
如:
procedure a;
begin
a;
end;
這種方式是直接調用.
又如:
procedure b;
begin
c;
end;
procedure c;
begin
b;
end;
這種方式是間接調用.
如何設計遞歸算法
1.確定遞歸公式
2.確定邊界(終了)條件
