Problem Description
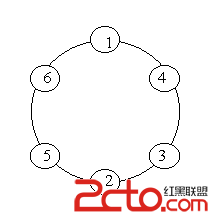
A ring is compose of n circles as shown in diagram. Put natural number 1, 2, ..., n into each circle separately, and the sum of numbers in two adjacent circles should be a prime.
Note: the number of first circle should always be 1.
Input
n (0 < n < 20).
Output
The output format is shown as sample below. Each row represents a series of circle numbers in the ring beginning from 1 clockwisely and anticlockwisely. The order of numbers must satisfy the above requirements. Print solutions in lexicographical order.
You are to write a program that completes above process.
Print a blank line after each case.
Sample Input
6
8
Sample Output
Case 1:
1 4 3 2 5 6
1 6 5 2 3 4
Case 2:
1 2 3 8 5 6 7 4
1 2 5 8 3 4 7 6
1 4 7 6 5 8 3 2
1 6 7 4 3 8 5 2
Source
Asia 1996, Shanghai (Mainland China)
Recommend
JGShining
[cpp]
/*********************************
* 日期：2013-3-14
* 作者：SJF0115
* 題號: HDU 題目1016: Prime Ring Problem
* 來源：http://acm.hdu.edu.cn/showproblem.php?pid=1016
* 結果：AC
* 來源：Asia 1996, Shanghai (Mainland China)
* 總結：
**********************************/
#include<stdio.h>
#include<string.h>
int prime[] = {0,0,1,1,0,1,0,1,0,0,0,1,0,1,0,0,0,1,0,1,0,0,0,1,0,0,0,0,0,1,0,1,0,0,0,0,0,1,0,0,0};
int visited[21];
int value[21];
int n;
void DFS(int step){
int i;
//最後一個數還需要和1判斷一下相加是否是素數
if(step == n+1){
if(prime[value[step - 1] + 1]){
//輸出素數環
for(i = 1;i <= n;i++){
printf("%d%c",value[i],i==n?'\n':' ');
}
}
}
else{
for(i = 2;i <= n;i++){
//該數據沒有使用過並且與前一個數相加為素數
if(!visited[i] && prime[i + value[step-1]]){
//標記已訪問
visited[i] = 1;
value[step] = i;
DFS(step+1);
visited[i] = 0;
}
}
}
}
int main(){
int caseNum = 1;
while(scanf("%d",&n) != EOF){
memset(visited,0,n);
printf("Case %d:\n",caseNum);
//素數環的第一個數永遠都是1
value[1] = 1;
DFS(2);
printf("\n");
caseNum ++;
}
return 0;
}
/*********************************
* 日期：2013-3-14
* 作者：SJF0115
* 題號: HDU 題目1016: Prime Ring Problem
* 來源：http://acm.hdu.edu.cn/showproblem.php?pid=1016
* 結果：AC
* 來源：Asia 1996, Shanghai (Mainland China)
* 總結：
**********************************/
#include<stdio.h>
#include<string.h>
int prime[] = {0,0,1,1,0,1,0,1,0,0,0,1,0,1,0,0,0,1,0,1,0,0,0,1,0,0,0,0,0,1,0,1,0,0,0,0,0,1,0,0,0};
int visited[21];
int value[21];
int n;
void DFS(int step){
int i;
//最後一個數還需要和1判斷一下相加是否是素數
if(step == n+1){
if(prime[value[step - 1] + 1]){
//輸出素數環
for(i = 1;i <= n;i++){
printf("%d%c",value[i],i==n?'\n':' ');
}
}
}
else{
for(i = 2;i <= n;i++){
//該數據沒有使用過並且與前一個數相加為素數
if(!visited[i] && prime[i + value[step-1]]){
//標記已訪問
visited[i] = 1;
value[step] = i;
DFS(step+1);
visited[i] = 0;
}
}
}
}
int main(){
int caseNum = 1;
while(scanf("%d",&n) != EOF){
memset(visited,0,n);
printf("Case %d:\n",caseNum);
//素數環的第一個數永遠都是1
value[1] = 1;
DFS(2);
printf("\n");
caseNum ++;
}
return 0;
}
