題目:給出一些牆,水從高往低流,每次只能到達一面牆,選擇一個路徑,使得路徑上的流量的最小值最大。
http://codeforces.com/problemset/problem/269/D
首先主要的是題意的理解問題。
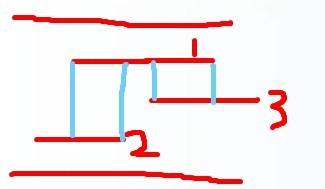 像上圖這種情況的話,1是可以流向2的,1也是可以流向3的。
我開始的理解是1不能流向2,因為中間有3的阻擋,其實只是看公共部分的。
像上圖這種情況的話,1是可以流向2的,1也是可以流向3的。
我開始的理解是1不能流向2,因為中間有3的阻擋,其實只是看公共部分的。
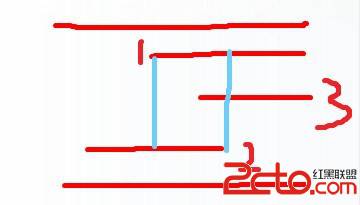 像這種情況1是不能流向2的,因為1和2的公共部分有3的阻擋。
理解這點之後,便好辦了。
按高度排序之後,將所有的坐標離散化。
按高度將線段插入到線段樹中,線段樹中維護這個區間最高的一條線段的標號,也就是標號的最大值。
像這種情況1是不能流向2的,因為1和2的公共部分有3的阻擋。
理解這點之後,便好辦了。
按高度排序之後,將所有的坐標離散化。
按高度將線段插入到線段樹中,線段樹中維護這個區間最高的一條線段的標號,也就是標號的最大值。
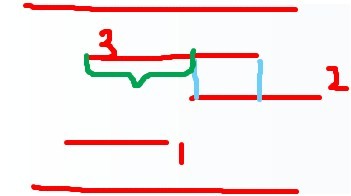
 對於線段3進行一次查詢之後,發現這段區間最後一次覆蓋的應該是線段2,但是線段3並非完全覆蓋於線段2的。
便可以繼續查詢綠色部分。
像左圖,查詢結果應該是線段1,所以3 是可以流向2,也是可以流向1的,這裡用dp做一次最優解就行了。
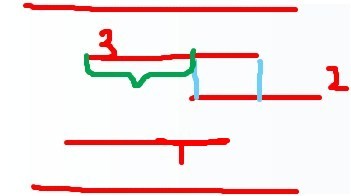
但是注意上面右圖的情況,查詢綠色部分,得到線段1,但是線段1的右端超過了綠色的右端,根據我們之前的查詢知道,綠色右端已經被2覆蓋,所以這時候要對兩端作一個標記,標明不能超過端點
[cpp]
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define test puts("OK");
#define inf 1000000000
#define lson (step<<1)
#define rson (step<<1|1)
using namespace std;
const int N=100005;
struct Wall{
int h,l,r;
Wall(){}
Wall(int _h,int _l,int _r):h(_h),l(_l),r(_r){}
bool operator<(const Wall w)const{
return h<w.h;
}
}wall[N];
struct Seg_Tree{
int left,right;
int val,all;
}L[N<<3];
int n,t;
int x[N<<1],cnt; //離散化
int dp[N]={0};
void Bulid(int step,int l,int r){
L[step].left=l;
L[step].right=r;
L[step].val=L[step].all=-1;
if(l==r) return ;
int m=(l+r)>>1;
Bulid(lson,l,m);
Bulid(rson,m+1,r);
}
void Push_Down(int step){
if(L[step].all!=-1){
L[lson].all=L[rson].all=L[step].all;
L[lson].val=L[rson].val=L[step].all;
L[step].all=-1;
}
}
void Push_Up(int step){
L[step].val=max(L[lson].val,L[rson].val);
}
void Update(int step,int l,int r,int id){
if(L[step].left==l&&L[step].right==r){
L[step].val=L[step].all=id;
return ;
}
Push_Down(step);
int m=(L[step].left+L[step].right)>>1;
if(r<=m) Update(lson,l,r,id);
else if(l>m) Update(rson,l,r,id);
else{
Update(lson,l,m,id);
Update(rson,m+1,r,id);
}
Push_Up(step);
}
int Query(int step,int l,int r){
if(L[step].left==l&&L[step].right==r)
return L[step].val;
int m=(L[step].left+L[step].right)>>1;
Push_Down(step);
if(r<=m) return Query(lson,l,r);
else if(l>m) return Query(rson,l,r);
else return max(Query(lson,l,m),Query(rson,m+1,r));
}
void slove(int l,int r,int who,int can_l,int can_r){
if(l>r) return ;
int id=Query(1,l,r);
if(id==-1){
Update(1,l,r,who);
dp[who]=x[r+1]-x[l];
return ;
}
int pre_l=wall[id].l,pre_r=wall[id].r;
if((pre_l>=l||can_l)&&(pre_r<=r||can_r)){
dp[who]=max(dp[who],min(dp[id],x[min(pre_r,r)+1]-x[max(pre_l,l)]));
}
if(l<pre_l) slove(l,pre_l-1,who,can_l,0);
if(r>pre_r) slove(pre_r+1,r,who,0,can_r);
}
int main(){
scanf("%d%d",&n,&t);
for(int i=0;i<n;i++){
int h,l,r;
scanf("%d%d%d",&h,&l,&r);
wall[i]=Wall(h,l,r);
x[i*2]=l;x[i*2+1]=r;
}
x[n*2]=-inf;x[n*2+1]=inf;
sort(x,x+2*n+2);
cnt=unique(x,x+2*n+2)-x;
wall[n++]=Wall(0,-inf,inf);
wall[n++]=Wall(t,-inf,inf);
sort(wall,wall+n);
for(int i=0;i<n;i++){
wall[i].l=lower_bound(x,x+cnt,wall[i].l)-x;
wall[i].r=lower_bound(x,x+cnt,wall[i].r)-x-1;
}
Bulid(1,0,cnt-1);
for(int i=0;i<n;i++){
int l=wall[i].l,r=wall[i].r;
slove(l,r,i,1,1);
Update(1,l,r,i);
}
printf("%d\n",dp[n-1]);
return 0;
}
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define test puts("OK");
#define inf 1000000000
#define lson (step<<1)
#define rson (step<<1|1)
using namespace std;
const int N=100005;
struct Wall{
int h,l,r;
Wall(){}
Wall(int _h,int _l,int _r):h(_h),l(_l),r(_r){}
bool operator<(const Wall w)const{
return h<w.h;
}
}wall[N];
struct Seg_Tree{
int left,right;
int val,all;
}L[N<<3];
int n,t;
int x[N<<1],cnt; //離散化
int dp[N]={0};
void Bulid(int step,int l,int r){
L[step].left=l;
L[step].right=r;
L[step].val=L[step].all=-1;
if(l==r) return ;
int m=(l+r)>>1;
Bulid(lson,l,m);
Bulid(rson,m+1,r);
}
void Push_Down(int step){
if(L[step].all!=-1){
L[lson].all=L[rson].all=L[step].all;
L[lson].val=L[rson].val=L[step].all;
L[step].all=-1;
}
}
void Push_Up(int step){
L[step].val=max(L[lson].val,L[rson].val);
}
void Update(int step,int l,int r,int id){
if(L[step].left==l&&L[step].right==r){
L[step].val=L[step].all=id;
return ;
}
Push_Down(step);
int m=(L[step].left+L[step].right)>>1;
if(r<=m) Update(lson,l,r,id);
else if(l>m) Update(rson,l,r,id);
else{
Update(lson,l,m,id);
Update(rson,m+1,r,id);
}
Push_Up(step);
}
int Query(int step,int l,int r){
if(L[step].left==l&&L[step].right==r)
return L[step].val;
int m=(L[step].left+L[step].right)>>1;
Push_Down(step);
if(r<=m) return Query(lson,l,r);
else if(l>m) return Query(rson,l,r);
else return max(Query(lson,l,m),Query(rson,m+1,r));
}
void slove(int l,int r,int who,int can_l,int can_r){
if(l>r) return ;
int id=Query(1,l,r);
if(id==-1){
Update(1,l,r,who);
dp[who]=x[r+1]-x[l];
return ;
}
int pre_l=wall[id].l,pre_r=wall[id].r;
if((pre_l>=l||can_l)&&(pre_r<=r||can_r)){
dp[who]=max(dp[who],min(dp[id],x[min(pre_r,r)+1]-x[max(pre_l,l)]));
}
if(l<pre_l) slove(l,pre_l-1,who,can_l,0);
if(r>pre_r) slove(pre_r+1,r,who,0,can_r);
}
int main(){
scanf("%d%d",&n,&t);
for(int i=0;i<n;i++){
int h,l,r;
scanf("%d%d%d",&h,&l,&r);
wall[i]=Wall(h,l,r);
x[i*2]=l;x[i*2+1]=r;
}
x[n*2]=-inf;x[n*2+1]=inf;
sort(x,x+2*n+2);
cnt=unique(x,x+2*n+2)-x;
wall[n++]=Wall(0,-inf,inf);
wall[n++]=Wall(t,-inf,inf);
sort(wall,wall+n);
for(int i=0;i<n;i++){
wall[i].l=lower_bound(x,x+cnt,wall[i].l)-x;
wall[i].r=lower_bound(x,x+cnt,wall[i].r)-x-1;
}
Bulid(1,0,cnt-1);
for(int i=0;i<n;i++){
int l=wall[i].l,r=wall[i].r;
slove(l,r,i,1,1);
Update(1,l,r,i);
}
printf("%d\n",dp[n-1]);
return 0;
}
對於線段3進行一次查詢之後,發現這段區間最後一次覆蓋的應該是線段2,但是線段3並非完全覆蓋於線段2的。
便可以繼續查詢綠色部分。
像左圖,查詢結果應該是線段1,所以3 是可以流向2,也是可以流向1的,這裡用dp做一次最優解就行了。
但是注意上面右圖的情況,查詢綠色部分,得到線段1,但是線段1的右端超過了綠色的右端,根據我們之前的查詢知道,綠色右端已經被2覆蓋,所以這時候要對兩端作一個標記,標明不能超過端點
[cpp]
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define test puts("OK");
#define inf 1000000000
#define lson (step<<1)
#define rson (step<<1|1)
using namespace std;
const int N=100005;
struct Wall{
int h,l,r;
Wall(){}
Wall(int _h,int _l,int _r):h(_h),l(_l),r(_r){}
bool operator<(const Wall w)const{
return h<w.h;
}
}wall[N];
struct Seg_Tree{
int left,right;
int val,all;
}L[N<<3];
int n,t;
int x[N<<1],cnt; //離散化
int dp[N]={0};
void Bulid(int step,int l,int r){
L[step].left=l;
L[step].right=r;
L[step].val=L[step].all=-1;
if(l==r) return ;
int m=(l+r)>>1;
Bulid(lson,l,m);
Bulid(rson,m+1,r);
}
void Push_Down(int step){
if(L[step].all!=-1){
L[lson].all=L[rson].all=L[step].all;
L[lson].val=L[rson].val=L[step].all;
L[step].all=-1;
}
}
void Push_Up(int step){
L[step].val=max(L[lson].val,L[rson].val);
}
void Update(int step,int l,int r,int id){
if(L[step].left==l&&L[step].right==r){
L[step].val=L[step].all=id;
return ;
}
Push_Down(step);
int m=(L[step].left+L[step].right)>>1;
if(r<=m) Update(lson,l,r,id);
else if(l>m) Update(rson,l,r,id);
else{
Update(lson,l,m,id);
Update(rson,m+1,r,id);
}
Push_Up(step);
}
int Query(int step,int l,int r){
if(L[step].left==l&&L[step].right==r)
return L[step].val;
int m=(L[step].left+L[step].right)>>1;
Push_Down(step);
if(r<=m) return Query(lson,l,r);
else if(l>m) return Query(rson,l,r);
else return max(Query(lson,l,m),Query(rson,m+1,r));
}
void slove(int l,int r,int who,int can_l,int can_r){
if(l>r) return ;
int id=Query(1,l,r);
if(id==-1){
Update(1,l,r,who);
dp[who]=x[r+1]-x[l];
return ;
}
int pre_l=wall[id].l,pre_r=wall[id].r;
if((pre_l>=l||can_l)&&(pre_r<=r||can_r)){
dp[who]=max(dp[who],min(dp[id],x[min(pre_r,r)+1]-x[max(pre_l,l)]));
}
if(l<pre_l) slove(l,pre_l-1,who,can_l,0);
if(r>pre_r) slove(pre_r+1,r,who,0,can_r);
}
int main(){
scanf("%d%d",&n,&t);
for(int i=0;i<n;i++){
int h,l,r;
scanf("%d%d%d",&h,&l,&r);
wall[i]=Wall(h,l,r);
x[i*2]=l;x[i*2+1]=r;
}
x[n*2]=-inf;x[n*2+1]=inf;
sort(x,x+2*n+2);
cnt=unique(x,x+2*n+2)-x;
wall[n++]=Wall(0,-inf,inf);
wall[n++]=Wall(t,-inf,inf);
sort(wall,wall+n);
for(int i=0;i<n;i++){
wall[i].l=lower_bound(x,x+cnt,wall[i].l)-x;
wall[i].r=lower_bound(x,x+cnt,wall[i].r)-x-1;
}
Bulid(1,0,cnt-1);
for(int i=0;i<n;i++){
int l=wall[i].l,r=wall[i].r;
slove(l,r,i,1,1);
Update(1,l,r,i);
}
printf("%d\n",dp[n-1]);
return 0;
}
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define test puts("OK");
#define inf 1000000000
#define lson (step<<1)
#define rson (step<<1|1)
using namespace std;
const int N=100005;
struct Wall{
int h,l,r;
Wall(){}
Wall(int _h,int _l,int _r):h(_h),l(_l),r(_r){}
bool operator<(const Wall w)const{
return h<w.h;
}
}wall[N];
struct Seg_Tree{
int left,right;
int val,all;
}L[N<<3];
int n,t;
int x[N<<1],cnt; //離散化
int dp[N]={0};
void Bulid(int step,int l,int r){
L[step].left=l;
L[step].right=r;
L[step].val=L[step].all=-1;
if(l==r) return ;
int m=(l+r)>>1;
Bulid(lson,l,m);
Bulid(rson,m+1,r);
}
void Push_Down(int step){
if(L[step].all!=-1){
L[lson].all=L[rson].all=L[step].all;
L[lson].val=L[rson].val=L[step].all;
L[step].all=-1;
}
}
void Push_Up(int step){
L[step].val=max(L[lson].val,L[rson].val);
}
void Update(int step,int l,int r,int id){
if(L[step].left==l&&L[step].right==r){
L[step].val=L[step].all=id;
return ;
}
Push_Down(step);
int m=(L[step].left+L[step].right)>>1;
if(r<=m) Update(lson,l,r,id);
else if(l>m) Update(rson,l,r,id);
else{
Update(lson,l,m,id);
Update(rson,m+1,r,id);
}
Push_Up(step);
}
int Query(int step,int l,int r){
if(L[step].left==l&&L[step].right==r)
return L[step].val;
int m=(L[step].left+L[step].right)>>1;
Push_Down(step);
if(r<=m) return Query(lson,l,r);
else if(l>m) return Query(rson,l,r);
else return max(Query(lson,l,m),Query(rson,m+1,r));
}
void slove(int l,int r,int who,int can_l,int can_r){
if(l>r) return ;
int id=Query(1,l,r);
if(id==-1){
Update(1,l,r,who);
dp[who]=x[r+1]-x[l];
return ;
}
int pre_l=wall[id].l,pre_r=wall[id].r;
if((pre_l>=l||can_l)&&(pre_r<=r||can_r)){
dp[who]=max(dp[who],min(dp[id],x[min(pre_r,r)+1]-x[max(pre_l,l)]));
}
if(l<pre_l) slove(l,pre_l-1,who,can_l,0);
if(r>pre_r) slove(pre_r+1,r,who,0,can_r);
}
int main(){
scanf("%d%d",&n,&t);
for(int i=0;i<n;i++){
int h,l,r;
scanf("%d%d%d",&h,&l,&r);
wall[i]=Wall(h,l,r);
x[i*2]=l;x[i*2+1]=r;
}
x[n*2]=-inf;x[n*2+1]=inf;
sort(x,x+2*n+2);
cnt=unique(x,x+2*n+2)-x;
wall[n++]=Wall(0,-inf,inf);
wall[n++]=Wall(t,-inf,inf);
sort(wall,wall+n);
for(int i=0;i<n;i++){
wall[i].l=lower_bound(x,x+cnt,wall[i].l)-x;
wall[i].r=lower_bound(x,x+cnt,wall[i].r)-x-1;
}
Bulid(1,0,cnt-1);
for(int i=0;i<n;i++){
int l=wall[i].l,r=wall[i].r;
slove(l,r,i,1,1);
Update(1,l,r,i);
}
printf("%d\n",dp[n-1]);
return 0;
}