1、問題描速:
設 S={x1, x2, ···, xn} 是一個有序集合,且x1, x2, ···, xn表示有序集合的二叉搜索樹利用二叉樹的頂點存儲有序集中的元素,而且具有性質:存儲於每個頂點中的元素x 大於其左子樹中任一個頂點中存儲的元素,小於其右子樹中任意頂點中存儲的元素。二叉樹中的葉頂點是形如(xi, xi+1) 的開區間。在表示S的二叉搜索樹中搜索一個元素x,返回的結果有兩種情形:
(1) 在二叉樹的內部頂點處找到: x = xi
(2) 在二叉樹的葉頂點中確定: x∈ (xi , xi+1)
設在情形(1)中找到元素x = xi的概率為bi;在情形(2)中確定x∈ (xi , xi+1)的概率為ai。其中約定x0= -∞ , xn+1= + ∞ ,有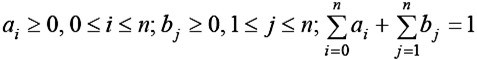 集合{a0,b1,a1,……bn,an}稱為集合S的存取概率分布。
最優二叉搜索樹:在一個表示S的二叉樹T中,設存儲元素xi的結點深度為ci;葉結點(xj,xj+1)的結點深度為dj。
集合{a0,b1,a1,……bn,an}稱為集合S的存取概率分布。
最優二叉搜索樹:在一個表示S的二叉樹T中,設存儲元素xi的結點深度為ci;葉結點(xj,xj+1)的結點深度為dj。
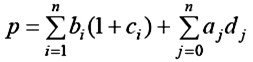 注:在檢索過程中,每進行一次比較,就進入下面一層,對於成功的檢索,比較的次數就是所在的層數加1。對於不成功的檢索,被檢索的關鍵碼屬於那個外部結點代表的可能關鍵碼集合,比較次數就等於此外部結點的層數。對於圖的內結點而言,第0層需要比較操作次數為1,第1層需要比較2次,第2層需要3次。
p表示在二叉搜索樹T中作一次搜索所需的平均比較次數。P又稱為二叉搜索樹T的平均路長,在一般情況下,不同的二叉搜索樹的平均路長是不同的。對於有序集S及其存取概率分布(a0,b1,a1,……bn,an),在所有表示有序集S的二叉搜索樹中找出一棵具有最小平均路長的二叉搜索樹。
設Pi是對ai檢索的概率。設qi是對滿足ai<X<ai+1,0<=i<=n的標識符X檢索的概率, (假定a0=--∞且an+1=+ ∞)。
注:在檢索過程中,每進行一次比較,就進入下面一層,對於成功的檢索,比較的次數就是所在的層數加1。對於不成功的檢索,被檢索的關鍵碼屬於那個外部結點代表的可能關鍵碼集合,比較次數就等於此外部結點的層數。對於圖的內結點而言,第0層需要比較操作次數為1,第1層需要比較2次,第2層需要3次。
p表示在二叉搜索樹T中作一次搜索所需的平均比較次數。P又稱為二叉搜索樹T的平均路長,在一般情況下,不同的二叉搜索樹的平均路長是不同的。對於有序集S及其存取概率分布(a0,b1,a1,……bn,an),在所有表示有序集S的二叉搜索樹中找出一棵具有最小平均路長的二叉搜索樹。
設Pi是對ai檢索的概率。設qi是對滿足ai<X<ai+1,0<=i<=n的標識符X檢索的概率, (假定a0=--∞且an+1=+ ∞)。
 對於有n個關鍵碼的集合,其關鍵碼有n!種不同的排列,可構成的不同二叉搜索樹有棵。(n個結點的不同二叉樹,卡塔蘭數)。如何評價這些二叉搜索樹,可以用樹的搜索效率來衡量。例如:標識符集{1, 2, 3}={do, if, stop}可能的二分檢索樹為:
對於有n個關鍵碼的集合,其關鍵碼有n!種不同的排列,可構成的不同二叉搜索樹有棵。(n個結點的不同二叉樹,卡塔蘭數)。如何評價這些二叉搜索樹,可以用樹的搜索效率來衡量。例如:標識符集{1, 2, 3}={do, if, stop}可能的二分檢索樹為:
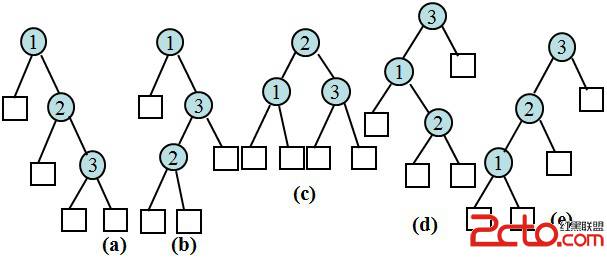 若P1=0.5, P2=0.1, P3=0.05,q0=0.15, q1=0.1, q2=0.05, q3=0.05,求每棵樹的平均比較次數(成本)。
Pa(n)=1 × p1 + 2 × p2+3 × p3 + 1×q0 +2×q1+ 3×( q2 + q3 ) =1 × 0.5+ 2 × 0.1+3 ×0.05 + 1×0.05 +2×0.1+ 3×( 0.05 + 0.05 ) =1.5
Pb(n)=1 × p1 + 2 × p3+3 × p2 + 1×q0 + 3×( q2 + q3 ) =1 × 0.5+ 2 × 0.05 + 3 ×0.1 + 1×0.15 +2×0.05+ 3×( 0.05 + 0.05 ) =1.6
Pc(n)=1 × p2 + 2 × (p1 + p3) + 2×(q0 +q1 +q2 + q3 ) =1 × 0.1+ 2 × (0.5 + 0.05) + 2×(0.15 + 0.1 + 0.05 + 0.05) =1.9
Pd(n)=1 × p3 + 2 × p1+3 × p2 + 1 × q3+2 × q0 +3 × (q1+ q2) =1 × 0.05 + 2 × 0.5 + 3 × 0.1 + 1×0.05 + 2 × 0.15 + 3 × (0.1 + 0.05) =2.15
Pe(n)=1 × p3 + 2 × p1+3 × p2 + 1 × q3+2 × q0 +3 × (q1 + q2) =1 × 0.05 + 2 × 0.5 + 3 × 0.1 + 1×0.05 + 2 × 0.15 + 3 × (0.1 + 0.05) =2.15
因此,上例中的最小平均路長為Pa(n)=1.5。
可以得出結論:結點在二叉搜索樹中的層次越深,需要比較的次數就越多,因此要構造一棵最小二叉樹,一般盡量把搜索概率較高的結點放在較高的層次。
2、最優子結構性質:
假設選擇 k為樹根,則 1, 2, …, k-1 和a0, a1, …, ak-1 都將位於左子樹 L 上,其余結點 (k+1, …, n 和 ak, ak+1, …, an)位於右子樹 R 上。設COST(L) 和COST(R) 分別是二分檢索樹T的左子樹和右子樹的成本。則檢索樹T的成本是:P(k)+ COST(L) + COST(R) + …… 。若 T 是最優的,則上式及 COST(L) 和COST(R) 必定都取最小值。
證明:二叉搜索樹T 的一棵含有頂點xi , ··· , xj和葉頂點(xi-1 , xi ) , ··· , ( xj , xj+1)的子樹可以看作是有序集{ xi , ··· , xj}關於全集為 { xi-1 , xj+1 }的一棵二叉搜索樹(T自身可以看作是有序集) 。根據S 的存取分布概率,在子樹的頂點處被搜索到的概率是:。{xi , ··· , xj}的存儲概率分布為{ai-1, bi, …, bj, aj },其中,ah,bk分別是下面的條件概率:。
若P1=0.5, P2=0.1, P3=0.05,q0=0.15, q1=0.1, q2=0.05, q3=0.05,求每棵樹的平均比較次數(成本)。
Pa(n)=1 × p1 + 2 × p2+3 × p3 + 1×q0 +2×q1+ 3×( q2 + q3 ) =1 × 0.5+ 2 × 0.1+3 ×0.05 + 1×0.05 +2×0.1+ 3×( 0.05 + 0.05 ) =1.5
Pb(n)=1 × p1 + 2 × p3+3 × p2 + 1×q0 + 3×( q2 + q3 ) =1 × 0.5+ 2 × 0.05 + 3 ×0.1 + 1×0.15 +2×0.05+ 3×( 0.05 + 0.05 ) =1.6
Pc(n)=1 × p2 + 2 × (p1 + p3) + 2×(q0 +q1 +q2 + q3 ) =1 × 0.1+ 2 × (0.5 + 0.05) + 2×(0.15 + 0.1 + 0.05 + 0.05) =1.9
Pd(n)=1 × p3 + 2 × p1+3 × p2 + 1 × q3+2 × q0 +3 × (q1+ q2) =1 × 0.05 + 2 × 0.5 + 3 × 0.1 + 1×0.05 + 2 × 0.15 + 3 × (0.1 + 0.05) =2.15
Pe(n)=1 × p3 + 2 × p1+3 × p2 + 1 × q3+2 × q0 +3 × (q1 + q2) =1 × 0.05 + 2 × 0.5 + 3 × 0.1 + 1×0.05 + 2 × 0.15 + 3 × (0.1 + 0.05) =2.15
因此,上例中的最小平均路長為Pa(n)=1.5。
可以得出結論:結點在二叉搜索樹中的層次越深,需要比較的次數就越多,因此要構造一棵最小二叉樹,一般盡量把搜索概率較高的結點放在較高的層次。
2、最優子結構性質:
假設選擇 k為樹根,則 1, 2, …, k-1 和a0, a1, …, ak-1 都將位於左子樹 L 上,其余結點 (k+1, …, n 和 ak, ak+1, …, an)位於右子樹 R 上。設COST(L) 和COST(R) 分別是二分檢索樹T的左子樹和右子樹的成本。則檢索樹T的成本是:P(k)+ COST(L) + COST(R) + …… 。若 T 是最優的,則上式及 COST(L) 和COST(R) 必定都取最小值。
證明:二叉搜索樹T 的一棵含有頂點xi , ··· , xj和葉頂點(xi-1 , xi ) , ··· , ( xj , xj+1)的子樹可以看作是有序集{ xi , ··· , xj}關於全集為 { xi-1 , xj+1 }的一棵二叉搜索樹(T自身可以看作是有序集) 。根據S 的存取分布概率,在子樹的頂點處被搜索到的概率是:。{xi , ··· , xj}的存儲概率分布為{ai-1, bi, …, bj, aj },其中,ah,bk分別是下面的條件概率:。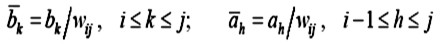 設Tij是有序集{xi , ··· , xj}關於存儲概率分布為{ai-1, bi, …, bj, aj}的一棵最優二叉搜索樹,其平均路長為pij,Tij的根頂點存儲的元素xm,其左子樹Tl和右子樹Tr的平均路長分別為pl和pr。由於Tl和Tr中頂點深度是它們在Tij中的深度減1,所以得到:
設Tij是有序集{xi , ··· , xj}關於存儲概率分布為{ai-1, bi, …, bj, aj}的一棵最優二叉搜索樹,其平均路長為pij,Tij的根頂點存儲的元素xm,其左子樹Tl和右子樹Tr的平均路長分別為pl和pr。由於Tl和Tr中頂點深度是它們在Tij中的深度減1,所以得到:
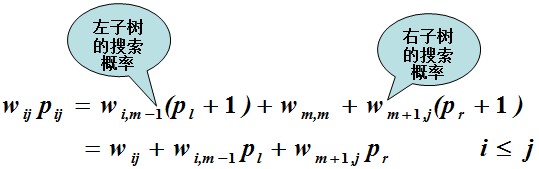 由於Ti是關於集合{xi , ··· , xm-1}的一棵二叉搜索樹,故Pl>=Pi,m-1。若Pl>Pi,m-1,則用Ti,m-1替換Tl可得到平均路長比Tij更小的二叉搜索樹。這與Tij是最優二叉搜索樹矛盾。故Tl是一棵最優二叉搜索樹。同理可證Tr也是一棵最優二叉搜索樹。因此最優二叉搜索樹問題具有最優子結構性質。
3、遞推關系:
根據最優二叉搜索樹問題的最優子結構性質可建立計算pij的遞歸式如下:
由於Ti是關於集合{xi , ··· , xm-1}的一棵二叉搜索樹,故Pl>=Pi,m-1。若Pl>Pi,m-1,則用Ti,m-1替換Tl可得到平均路長比Tij更小的二叉搜索樹。這與Tij是最優二叉搜索樹矛盾。故Tl是一棵最優二叉搜索樹。同理可證Tr也是一棵最優二叉搜索樹。因此最優二叉搜索樹問題具有最優子結構性質。
3、遞推關系:
根據最優二叉搜索樹問題的最優子結構性質可建立計算pij的遞歸式如下:
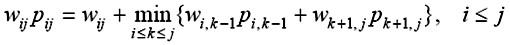 初始時:
初始時: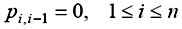 記 wi,j pi,j為m(i,j) ,則m(1,n)=w1,n p1,n=p1,n為所求的最優值。計算m(i,j)的遞歸式為:
記 wi,j pi,j為m(i,j) ,則m(1,n)=w1,n p1,n=p1,n為所求的最優值。計算m(i,j)的遞歸式為:
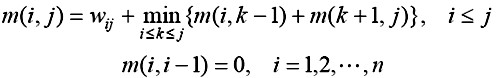 4、求解過程:
1)沒有內部節點時,構造T[1][0],T[2][1],T[3][2]……,T[n+1][n]
2)構造只有1個內部結點的最優二叉搜索樹T[1][1],T[2][2]…, T[n][n],可以求得m[i][i] 同時可以用一個數組存做根結點元素為:s[1][1]=1, s[2][2]=2…s[n][n]=n
3)構造具有2個、3個、……、n個內部結點的最優二叉搜索樹。
……
r ( 起止下標的差)
0 T[1][1], T[2][2] , …, T[n][n],
1 T[1][2], T[2][3], …,T[n-1][n],
2 T[1][3], T[2][4], …,T[n-2][n],
……
r T[1][r+1], T[2][r+2], …,T[i][i+r],…,T[n-r][n]
……
n-1 T[1][n]
具體代碼如下:
[cpp]
//3d11-1 最優二叉搜索樹 動態規劃
#include "stdafx.h"
#include <iostream>
using namespace std;
const int N = 3;
void OptimalBinarySearchTree(double a[],double b[],int n,double **m,int **s,double **w);
void Traceback(int n,int i,int j,int **s,int f,char ch);
int main()
{
double a[] = {0.15,0.1,0.05,0.05};
double b[] = {0.00,0.5,0.1,0.05};
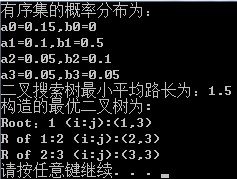
cout<<"有序集的概率分布為:"<<endl;
for(int i=0; i<N+1; i++)
{
cout<<"a"<<i<<"="<<a[i]<<",b"<<i<<"="<<b[i]<<endl;
}
double **m = new double *[N+2];
int **s = new int *[N+2];
double **w =new double *[N+2];
for(int i=0;i<N+2;i++)
{
m[i] = new double[N+2];
s[i] = new int[N+2];
w[i] = new double[N+2];
}
OptimalBinarySearchTree(a,b,N,m,s,w);
cout<<"二叉搜索樹最小平均路長為:"<<m[1][N]<<endl;
cout<<"構造的最優二叉樹為:"<<endl;
Traceback(N,1,N,s,0,'0');
for(int i=0;i<N+2;i++)
{
delete m[i];
delete s[i];
delete w[i];
}
delete[] m;
delete[] s;
delete[] w;
return 0;
}
void OptimalBinarySearchTree(double a[],double b[],int n,double **m,int **s,double **w)
{
//初始化構造無內部節點的情況
for(int i=0; i<=n; i++)
{
w[i+1][i] = a[i];
m[i+1][i] = 0;
}
for(int r=0; r<n; r++)//r代表起止下標的差
{
for(int i=1; i<=n-r; i++)//i為起始元素下標
{
int j = i+r;//j為終止元素下標
//構造T[i][j] 填寫w[i][j],m[i][j],s[i][j]
//首選i作為根,其左子樹為空,右子樹為節點
w[i][j]=w[i][j-1]+a[j]+b[j];
m[i][j]=m[i+1][j];
s[i][j]=i;
//不選i作為根,設k為其根,則k=i+1,……j
//左子樹為節點:i,i+1……k-1,右子樹為節點:k+1,k+2,……j
for(int k=i+1; k<=j; k++)
{
double t = m[i][k-1]+m[k+1][j];
if(t<m[i][j])
{
m[i][j]=t;
s[i][j]=k;//根節點元素
}
}
m[i][j]+=w[i][j];
}
}
}
void Traceback(int n,int i,int j,int **s,int f,char ch)
{
int k=s[i][j];
if(k>0)
{
if(f==0)
{
//根
cout<<"Root:"<<k<<" (i:j):("<<i<<","<<j<<")"<<endl;
}
else
{
//子樹
cout<<ch<<" of "<<f<<":"<<k<<" (i:j):("<<i<<","<<j<<")"<<endl;
}
int t = k-1;
if(t>=i && t<=n)
{
//回溯左子樹
Traceback(n,i,t,s,k,'L');
}
t=k+1;
if(t<=j)
{
//回溯右子樹
Traceback(n,t,j,s,k,'R');
}
}
}
4、構造最優解:
算法OptimalBinarySearchTree中用s[i][j]保存最優子樹T(i,j)的根節點中的元素。當s[i][n]=k時,xk為所求二叉搜索樹根節點元素。其左子樹為T(1,k-1)。因此,i=s[1][k-1]表示T(1,k-1)的根節點元素為xi。依次類推,容易由s記錄的信息在O(n)時間內構造出所求的最優二叉搜索樹。
5、復雜度分析與優化:
算法中用到3個數組m,s和w,故所需空間復雜度為O(n^2)。算法的主要計算量在於計算。對於固定的r,它需要的計算時間O(j-i+1)=O(r+1)。因此算法所耗費的總時間為:。事實上,由《動態規劃加速原理之四邊形不等式》可以得到:而此狀態轉移方程的時間復雜度為O(n^2)。由此,對算法改進後的代碼如下:
[cpp]
//3d11-1 最優二叉搜索樹 動態規劃加速原理 四邊形不等式
#include "stdafx.h"
#include <iostream>
using namespace std;
const int N = 3;
void OptimalBinarySearchTree(double a[],double b[],int n,double **m,int **s,double **w);
void Traceback(int n,int i,int j,int **s,int f,char ch);
int main()
{
double a[] = {0.15,0.1,0.05,0.05};
double b[] = {0.00,0.5,0.1,0.05};
cout<<"有序集的概率分布為:"<<endl;
for(int i=0; i<N+1; i++)
{
cout<<"a"<<i<<"="<<a[i]<<",b"<<i<<"="<<b[i]<<endl;
}
double **m = new double *[N+2];
int **s = new int *[N+2];
double **w =new double *[N+2];
for(int i=0;i<N+2;i++)
{
m[i] = new double[N+2];
s[i] = new int[N+2];
w[i] = new double[N+2];
}
OptimalBinarySearchTree(a,b,N,m,s,w);
cout<<"二叉搜索樹最小平均路長為:"<<m[1][N]<<endl;
cout<<"構造的最優二叉樹為:"<<endl;
Traceback(N,1,N,s,0,'0');
for(int i=0;i<N+2;i++)
{
delete m[i];
delete s[i];
delete w[i];
}
delete[] m;
delete[] s;
delete[] w;
return 0;
}
void OptimalBinarySearchTree(double a[],double b[],int n,double **m,int **s,double **w)
{
//初始化構造無內部節點的情況
for(int i=0; i<=n; i++)
{
w[i+1][i] = a[i];
m[i+1][i] = 0;
s[i+1][i] = 0;
}
for(int r=0; r<n; r++)//r代表起止下標的差
{
for(int i=1; i<=n-r; i++)//i為起始元素下標
{
int j = i+r;//j為終止元素下標
int i1 = s[i][j-1]>i?s[i][j-1]:i;
int j1 = s[i+1][j]>i?s[i+1][j]:j;
//構造T[i][j] 填寫w[i][j],m[i][j],s[i][j]
//首選i作為根,其左子樹為空,右子樹為節點
w[i][j]=w[i][j-1]+a[j]+b[j];
m[i][j]=m[i][i1-1]+m[i1+1][j];
s[i][j]=i1;
//不選i作為根,設k為其根,則k=i+1,……j
//左子樹為節點:i,i+1……k-1,右子樹為節點:k+1,k+2,……j
for(int k=i1+1; k<=j1; k++)
{
double t = m[i][k-1]+m[k+1][j];
if(t<m[i][j])
{
m[i][j]=t;
s[i][j]=k;//根節點元素
}
}
m[i][j]+=w[i][j];
}
}
}
void Traceback(int n,int i,int j,int **s,int f,char ch)
{
int k=s[i][j];
if(k>0)
{
if(f==0)
{
//根
cout<<"Root:"<<k<<" (i:j):("<<i<<","<<j<<")"<<endl;
}
else
{
//子樹
cout<<ch<<" of "<<f<<":"<<k<<" (i:j):("<<i<<","<<j<<")"<<endl;
}
int t = k-1;
if(t>=i && t<=n)
{
//回溯左子樹
Traceback(n,i,t,s,k,'L');
}
t=k+1;
if(t<=j)
{
//回溯右子樹
Traceback(n,t,j,s,k,'R');
}
}
}
運行結果如圖:
4、求解過程:
1)沒有內部節點時,構造T[1][0],T[2][1],T[3][2]……,T[n+1][n]
2)構造只有1個內部結點的最優二叉搜索樹T[1][1],T[2][2]…, T[n][n],可以求得m[i][i] 同時可以用一個數組存做根結點元素為:s[1][1]=1, s[2][2]=2…s[n][n]=n
3)構造具有2個、3個、……、n個內部結點的最優二叉搜索樹。
……
r ( 起止下標的差)
0 T[1][1], T[2][2] , …, T[n][n],
1 T[1][2], T[2][3], …,T[n-1][n],
2 T[1][3], T[2][4], …,T[n-2][n],
……
r T[1][r+1], T[2][r+2], …,T[i][i+r],…,T[n-r][n]
……
n-1 T[1][n]
具體代碼如下:
[cpp]
//3d11-1 最優二叉搜索樹 動態規劃
#include "stdafx.h"
#include <iostream>
using namespace std;
const int N = 3;
void OptimalBinarySearchTree(double a[],double b[],int n,double **m,int **s,double **w);
void Traceback(int n,int i,int j,int **s,int f,char ch);
int main()
{
double a[] = {0.15,0.1,0.05,0.05};
double b[] = {0.00,0.5,0.1,0.05};
cout<<"有序集的概率分布為:"<<endl;
for(int i=0; i<N+1; i++)
{
cout<<"a"<<i<<"="<<a[i]<<",b"<<i<<"="<<b[i]<<endl;
}
double **m = new double *[N+2];
int **s = new int *[N+2];
double **w =new double *[N+2];
for(int i=0;i<N+2;i++)
{
m[i] = new double[N+2];
s[i] = new int[N+2];
w[i] = new double[N+2];
}
OptimalBinarySearchTree(a,b,N,m,s,w);
cout<<"二叉搜索樹最小平均路長為:"<<m[1][N]<<endl;
cout<<"構造的最優二叉樹為:"<<endl;
Traceback(N,1,N,s,0,'0');
for(int i=0;i<N+2;i++)
{
delete m[i];
delete s[i];
delete w[i];
}
delete[] m;
delete[] s;
delete[] w;
return 0;
}
void OptimalBinarySearchTree(double a[],double b[],int n,double **m,int **s,double **w)
{
//初始化構造無內部節點的情況
for(int i=0; i<=n; i++)
{
w[i+1][i] = a[i];
m[i+1][i] = 0;
}
for(int r=0; r<n; r++)//r代表起止下標的差
{
for(int i=1; i<=n-r; i++)//i為起始元素下標
{
int j = i+r;//j為終止元素下標
//構造T[i][j] 填寫w[i][j],m[i][j],s[i][j]
//首選i作為根,其左子樹為空,右子樹為節點
w[i][j]=w[i][j-1]+a[j]+b[j];
m[i][j]=m[i+1][j];
s[i][j]=i;
//不選i作為根,設k為其根,則k=i+1,……j
//左子樹為節點:i,i+1……k-1,右子樹為節點:k+1,k+2,……j
for(int k=i+1; k<=j; k++)
{
double t = m[i][k-1]+m[k+1][j];
if(t<m[i][j])
{
m[i][j]=t;
s[i][j]=k;//根節點元素
}
}
m[i][j]+=w[i][j];
}
}
}
void Traceback(int n,int i,int j,int **s,int f,char ch)
{
int k=s[i][j];
if(k>0)
{
if(f==0)
{
//根
cout<<"Root:"<<k<<" (i:j):("<<i<<","<<j<<")"<<endl;
}
else
{
//子樹
cout<<ch<<" of "<<f<<":"<<k<<" (i:j):("<<i<<","<<j<<")"<<endl;
}
int t = k-1;
if(t>=i && t<=n)
{
//回溯左子樹
Traceback(n,i,t,s,k,'L');
}
t=k+1;
if(t<=j)
{
//回溯右子樹
Traceback(n,t,j,s,k,'R');
}
}
}
4、構造最優解:
算法OptimalBinarySearchTree中用s[i][j]保存最優子樹T(i,j)的根節點中的元素。當s[i][n]=k時,xk為所求二叉搜索樹根節點元素。其左子樹為T(1,k-1)。因此,i=s[1][k-1]表示T(1,k-1)的根節點元素為xi。依次類推,容易由s記錄的信息在O(n)時間內構造出所求的最優二叉搜索樹。
5、復雜度分析與優化:
算法中用到3個數組m,s和w,故所需空間復雜度為O(n^2)。算法的主要計算量在於計算。對於固定的r,它需要的計算時間O(j-i+1)=O(r+1)。因此算法所耗費的總時間為:。事實上,由《動態規劃加速原理之四邊形不等式》可以得到:而此狀態轉移方程的時間復雜度為O(n^2)。由此,對算法改進後的代碼如下:
[cpp]
//3d11-1 最優二叉搜索樹 動態規劃加速原理 四邊形不等式
#include "stdafx.h"
#include <iostream>
using namespace std;
const int N = 3;
void OptimalBinarySearchTree(double a[],double b[],int n,double **m,int **s,double **w);
void Traceback(int n,int i,int j,int **s,int f,char ch);
int main()
{
double a[] = {0.15,0.1,0.05,0.05};
double b[] = {0.00,0.5,0.1,0.05};
cout<<"有序集的概率分布為:"<<endl;
for(int i=0; i<N+1; i++)
{
cout<<"a"<<i<<"="<<a[i]<<",b"<<i<<"="<<b[i]<<endl;
}
double **m = new double *[N+2];
int **s = new int *[N+2];
double **w =new double *[N+2];
for(int i=0;i<N+2;i++)
{
m[i] = new double[N+2];
s[i] = new int[N+2];
w[i] = new double[N+2];
}
OptimalBinarySearchTree(a,b,N,m,s,w);
cout<<"二叉搜索樹最小平均路長為:"<<m[1][N]<<endl;
cout<<"構造的最優二叉樹為:"<<endl;
Traceback(N,1,N,s,0,'0');
for(int i=0;i<N+2;i++)
{
delete m[i];
delete s[i];
delete w[i];
}
delete[] m;
delete[] s;
delete[] w;
return 0;
}
void OptimalBinarySearchTree(double a[],double b[],int n,double **m,int **s,double **w)
{
//初始化構造無內部節點的情況
for(int i=0; i<=n; i++)
{
w[i+1][i] = a[i];
m[i+1][i] = 0;
s[i+1][i] = 0;
}
for(int r=0; r<n; r++)//r代表起止下標的差
{
for(int i=1; i<=n-r; i++)//i為起始元素下標
{
int j = i+r;//j為終止元素下標
int i1 = s[i][j-1]>i?s[i][j-1]:i;
int j1 = s[i+1][j]>i?s[i+1][j]:j;
//構造T[i][j] 填寫w[i][j],m[i][j],s[i][j]
//首選i作為根,其左子樹為空,右子樹為節點
w[i][j]=w[i][j-1]+a[j]+b[j];
m[i][j]=m[i][i1-1]+m[i1+1][j];
s[i][j]=i1;
//不選i作為根,設k為其根,則k=i+1,……j
//左子樹為節點:i,i+1……k-1,右子樹為節點:k+1,k+2,……j
for(int k=i1+1; k<=j1; k++)
{
double t = m[i][k-1]+m[k+1][j];
if(t<m[i][j])
{
m[i][j]=t;
s[i][j]=k;//根節點元素
}
}
m[i][j]+=w[i][j];
}
}
}
void Traceback(int n,int i,int j,int **s,int f,char ch)
{
int k=s[i][j];
if(k>0)
{
if(f==0)
{
//根
cout<<"Root:"<<k<<" (i:j):("<<i<<","<<j<<")"<<endl;
}
else
{
//子樹
cout<<ch<<" of "<<f<<":"<<k<<" (i:j):("<<i<<","<<j<<")"<<endl;
}
int t = k-1;
if(t>=i && t<=n)
{
//回溯左子樹
Traceback(n,i,t,s,k,'L');
}
t=k+1;
if(t<=j)
{
//回溯右子樹
Traceback(n,t,j,s,k,'R');
}
}
}
運行結果如圖: