一般情況下矩陣乘法需要三個for循環，時間復雜度為O(n^3)，現在我們將矩陣分塊如圖：( 來自MIT算法導論 )
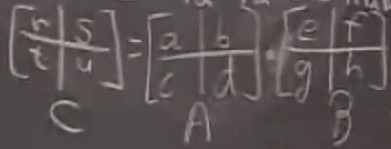一般算法需要八次乘法
r = a * e + b * g ;
s = a * f + b * h ;
t = c * e + d * g;
u = c * f + d * h;
strassen將其變成7次乘法，因為大家都知道乘法比加減法消耗更多，所有時間復雜更高！
strassen的處理是：
令：
p1 = a * ( f - h )
p2 = ( a + b ) * h
p3 = ( c +d ) * e
p4 = d * ( g - e )
p5 = ( a + d ) * ( e + h )
p6 = ( b - d ) * ( g + h )
p7 = ( a - c ) * ( e + f )
那麼我們可以知道：
r = p5 + p4 + p6 - p2
s = p1 + p2
t = p3 + p4
u = p5 + p1 - p3 - p7
我們可以看到上面只有7次乘法和多次加減法，最終達到降低復雜度為O( n^lg7 ) ~= O( n^2.81 );
代碼實現如下：
[cpp]
// strassen 算法：將矩陣相乘的復雜度降到O(n^lg7) ~= O(n^2.81)
// 原理是將8次乘法減少到7次的處理
// 現在理論上的最好的算法是O(n^2,367)，僅僅是理論上的而已
//
//
// 下面的代碼僅僅是簡單的實例而已，不必較真哦，呵呵~
// 下面的空間可以優化的，此處就不麻煩了~
#include <stdio.h>
#define N 10
//matrix + matrix
void plus( int t[N/2][N/2], int r[N/2][N/2], int s[N/2][N/2] )
{
int i, j;
for( i = 0; i < N / 2; i++ )
{
for( j = 0; j < N / 2; j++ )
{
t[i][j] = r[i][j] + s[i][j];
}
}
}
//matrix - matrix
void minus( int t[N/2][N/2], int r[N/2][N/2], int s[N/2][N/2] )
{
int i, j;
for( i = 0; i < N / 2; i++ )
{
for( j = 0; j < N / 2; j++ )
{
t[i][j] = r[i][j] - s[i][j];
}
}
}
//matrix * matrix
void mul( int t[N/2][N/2], int r[N/2][N/2], int s[N/2][N/2] )
{
int i, j, k;
for( i = 0; i < N / 2; i++ )
{
for( j = 0; j < N / 2; j++ )
{
t[i][j] = 0;
for( k = 0; k < N / 2; k++ )
{
t[i][j] += r[i][k] * s[k][j];
}
}
}
}
int main()
{
int i, j, k;
int mat[N][N];
int m1[N][N];
int m2[N][N];
int a[N/2][N/2],b[N/2][N/2],c[N/2][N/2],d[N/2][N/2];
int e[N/2][N/2],f[N/2][N/2],g[N/2][N/2],h[N/2][N/2];
int p1[N/2][N/2],p2[N/2][N/2],p3[N/2][N/2],p4[N/2][N/2];
int p5[N/2][N/2],p6[N/2][N/2],p7[N/2][N/2];
int r[N/2][N/2], s[N/2][N/2], t[N/2][N/2], u[N/2][N/2], t1[N/2][N/2], t2[N/2][N/2];
printf("\nInput the first matrix...:\n");
for( i = 0; i < N; i++ )
{
for( j = 0; j < N; j++ )
{
scanf("%d", &m1[i][j]);
}
}
printf("\nInput the second matrix...:\n");
for( i = 0; i < N; i++ )
{
for( j = 0; j < N; j++ )
{
scanf("%d", &m2[i][j]);
}
}
// a b c d e f g h
for( i = 0; i < N / 2; i++ )
{
for( j = 0; j < N / 2; j++ )
{
a[i][j] = m1[i][j];
b[i][j] = m1[i][j + N / 2];
c[i][j] = m1[i + N / 2][j];
d[i][j] = m1[i + N / 2][j + N / 2];
e[i][j] = m2[i][j];
f[i][j] = m2[i][j + N / 2];
g[i][j] = m2[i + N / 2][j];
h[i][j] = m2[i + N / 2][j + N / 2];
}
}
//p1
minus( r, f, h );
mul( p1, a, r );
//p2
plus( r, a, b );
mul( p2, r, h );
//p3
plus( r, c, d );
mul( p3, r, e );
//p4
minus( r, g, e );
mul( p4, d, r );
//p5
plus( r, a, d );
plus( s, e, f );
mul( p5, r, s );
//p6
minus( r, b, d );
plus( s, g, h );
mul( p6, r, s );
//p7
minus( r, a, c );
plus( s, e, f );
mul( p7, r, s );
//r = p5 + p4 - p2 + p6
plus( t1, p5, p4 );
minus( t2, t1, p2 );
plus( r, t2, p6 );
//s = p1 + p2
plus( s, p1, p2 );
//t = p3 + p4
plus( t, p3, p4 );
//u = p5 + p1 - p3 - p7 = p5 + p1 - ( p3 + p7 )
plus( t1, p5, p1 );
plus( t2, p3, p7 );
minus( u, t1, t2 );
for( i = 0; i < N / 2; i++ )
{
for( j = 0; j < N / 2; j++ )
{
mat[i][j] = r[i][j];
mat[i][j + N / 2] = s[i][j];
mat[i + N / 2][j] = t[i][j];
mat[i + N / 2][j + N / 2] = u[i][j];
}
}
printf("\n下面是strassen算法處理結果：\n");
for( i = 0; i < N; i++ )
{
for( j = 0; j < N; j++ )
{
printf("%d ", mat[i][j]);
}
printf("\n");
}
//下面是樸素算法處理
printf("\n下面是樸素算法處理結果：\n");
for( i = 0; i < N; i++ )
{
for( j = 0; j < N; j++ )
{
mat[i][j] = 0;
for( k = 0; k < N; k++ )
{
mat[i][j] += m1[i][j] * m2[i][j];
}
}
}
for( i = 0; i < N; i++ )
{
for( j = 0; j < N; j++ )
{
printf("%d ", mat[i][j]);
}
printf("\n");
}
return 0;
}
現在最好的計算矩陣乘法的復雜度是O( n^2.376 )，不過只是理論上的結果。此處僅僅做參考~
