對一個帶權有向圖G=(V,E),給定一個源頂點S,找出S到圖中其他頂點v的最短路徑即單源最短路徑問題。該問題還有很多變體,像單終點最短路徑、單對頂點最短路徑、每對頂點間的最短路徑等等。
最短路徑問題是具有最優子結構的:一對頂點間的最短路徑包含了該路徑上的頂點間的最短路徑。直觀上理解,如果該路徑上的兩個頂點間的路徑pij不是最短路徑,那麼用這兩個頂點間的最短路徑代替pij,那麼就會出現一條更短的路徑,與前面所說的最短路徑矛盾。(具體證明參見算法導論P358)。
需要說明的是負權值邊和松弛技術。Dijkstra算法是不允許圖中存在負權邊的,否則無法得到正確的結果。而Bellman-ford算法就允許圖中存在負權邊,而且該算法可以檢測圖中是否存在負權回路。兩種算法都用到了松弛技術。即對邊(u,v),如果通過u到達v比當前找到的到v的最短路徑還短,那麼就更新d[v]、parent[v]。通過松弛,可以減小最短路徑估計。
Bellman-ford算法:
因為圖中任意兩個頂點的最短路徑最多包含|V|-1條邊,所以至多對每條邊進行|V|-1次松弛後就會得到任意兩個頂點間的實際最短路徑。如果還能通過松弛降低最短路徑估計,那麼就可以斷定圖中存在負權回路,因為如果從s到v的路徑中包含負權回路,那麼s到v的最短路徑長度就是負無窮了。可以這樣理解,第i(i>=1)次松弛得到的是源點s到每個頂點vV的路徑長度為i的最短路徑,第|V|-1次松弛得到的就是長度為|V|-1的最短路徑。不過,顯然不是每個頂點到s的最短路徑長度都是|V|-1,所以對每條邊都進行|V|-1次松弛操作是沒有必要的。Bellman-ford的時間復雜度為O(VE)。可以對該算法進行簡單的優化,如果本次循環並未對任何一條邊進行松弛,那麼可以判定已經得到了最終結果,退出循環。
如圖所示:

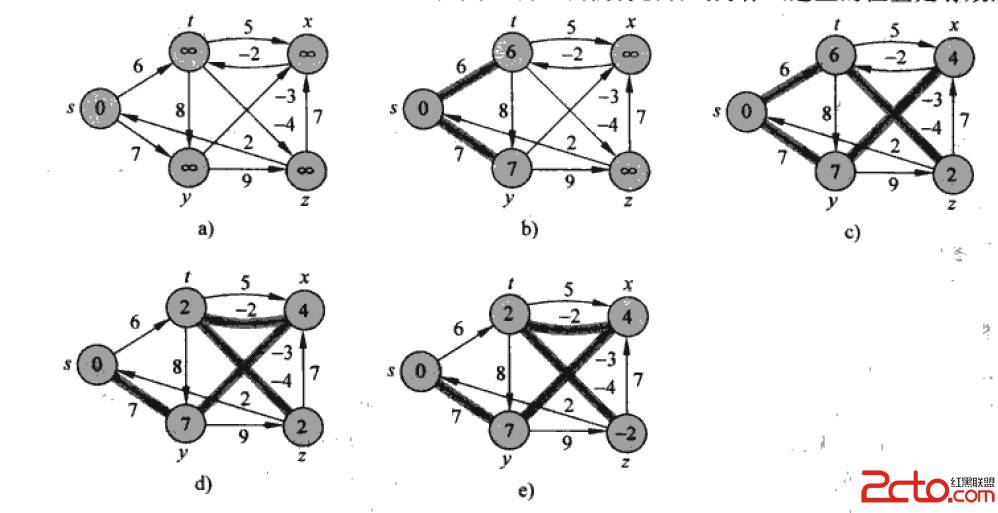
代碼如下:
[cpp]
#include<iostream>
#include<list>
using namespace std;
#define MAXVALUE 10000 //定義一個最長路徑
//此處Prim算法的圖為有向圖
struct Edge
{
int verno; //鄰接數組中節點編號
int weight; //權值
Edge* next; //指向下一條邊
};
struct Vertex
{
Edge *adj; //所指向的節點所在邊
int verno; //鄰接數組中節點編號
char key; //關鍵字
};
struct Graph
{
Vertex *vertexs; //節點數組
int vertexnum; //節點個數
int adjnum; //邊數
};
class MSWBellmanFord
{
public:
MSWBellmanFord(char *vertex,int vernum,char adj[][2],int *weight,int adjnum);
void BellmanInsert(int source,int dest,int weight);
int BellmanFindKey(char key);
void BellmanInitSingleSource();
bool BellmanMSW(char sourceKey);
void BellmanOutput();
private:
int *swayweight;
int *parent;
Graph *bfordGraph;
};
MSWBellmanFord::MSWBellmanFord(char *vertex,int vernum,char adj[][2],int *weight,int adjnum)
{
int i,source,dest;
swayweight = new int[vernum];
parent = new int[vernum];
bfordGraph = new Graph;
bfordGraph->vertexs = new Vertex[vernum];
bfordGraph->adjnum = adjnum;
bfordGraph->vertexnum = vernum;
for(i = 0;i < vernum;i++)
{
bfordGraph->vertexs[i].key = vertex[i];
bfordGraph->vertexs[i].verno = i;
bfordGraph->vertexs[i].adj = NULL;
}
for(i = 0;i < adjnum;i++)
{
source = BellmanFindKey(adj[i][0]);
dest = BellmanFindKey(adj[i][1]);
BellmanInsert(source,dest,weight[i]);
//BellmanInsert(dest,source,weight[i]); //無向圖與有向圖的區別在此
}
}
void MSWBellmanFord::BellmanInsert(int source,int dest,int weight)
{
if(bfordGraph->vertexs[source].adj == NULL || bfordGraph->vertexs[source].adj->weight > weight)
{
Edge* newnode = new Edge;
newnode->verno = dest;
newnode->weight = weight;
newnode->next = bfordGraph->vertexs[source].adj;
bfordGraph->vertexs[source].adj = newnode;
}
else
{
Edge* temp = bfordGraph->vertexs[source].adj;
while(temp->next != NULL) //插入新邊的時候,把權值從低到高進行排序
{
if(temp->next->weight > weight)
break;
temp = temp->next;
}
Edge* newnode = new Edge;
newnode->verno = dest;
newnode->weight = weight;
newnode->next = temp->next;
temp->next = newnode;
}
}
int MSWBellmanFord::BellmanFindKey(char key)
{
int i;
for(i = 0;i < bfordGraph->vertexnum;i++)
{
if(bfordGraph->vertexs[i].key == key)
break;
}
return i;
}
void MSWBellmanFord::BellmanInitSingleSource()
{
int vernum = bfordGraph->vertexnum;
for(int i = 0;i < vernum;i++)
{
swayweight[i] = MAXVALUE;
parent[i] = i;
}
}
bool MSWBellmanFord::BellmanMSW(char sourceKey)
{
int location = BellmanFindKey(sourceKey);
int vernum = bfordGraph->vertexnum;
int i,j;
Edge *temp;
BellmanInitSingleSource();
//swayweight[0] = 0; //這裡為了偷懶,沒有隨意指定source,location本來是代表source的下標的
swayweight[location] = 0;
for(i = 0;i < vernum; i++)
{
/*
for(j = 0;j < vernum; j++)
{
temp = bfordGraph->vertexs[j].adj;
while(temp != NULL)
{
if((temp->weight + swayweight[j]) < swayweight[temp->verno])
{
swayweight[temp->verno] = temp->weight + swayweight[j];
parent[temp->verno] = j;
}
temp = temp->next;
}
}
*/
temp = bfordGraph->vertexs[location].adj;
while(temp != NULL)
{
if((temp->weight + swayweight[location]) < swayweight[temp->verno])
{
swayweight[temp->verno] = temp->weight + swayweight[location];
parent[temp->verno] = location;
}
temp = temp->next;
}
j = (location + 1) % vernum;
while(j != location)
{
temp = bfordGraph->vertexs[j].adj;
while(temp != NULL)
{
if((temp->weight + swayweight[j]) < swayweight[temp->verno])
{
swayweight[temp->verno] = temp->weight + swayweight[j];
parent[temp->verno] = j;
}
temp = temp->next;
}
j = (j + 1) % vernum;
}
}
for(j = 0;j < vernum; j++)
{
temp = bfordGraph->vertexs[j].adj;
while(temp != NULL)
{
if((temp->weight + swayweight[j]) < swayweight[temp->verno])
{
return false;
}
temp = temp->next;
}
}
return true;
}
void MSWBellmanFord::BellmanOutput()
{
int i,j,weight;
list<int> route;
cout<<"All the most shortest route from source : "<<endl;
for(i = 0;i < bfordGraph->vertexnum;i++)
{
j = i;
weight = swayweight[j];
do
{
route.push_front(j);
j = parent[j];
}while(parent[j] != j);
cout<<bfordGraph->vertexs[j].key;
cout<<"---"<<bfordGraph->vertexs[route.front()].key;
route.pop_front();
while(!route.empty())
{
if(route.front() != j)
cout<<"---"<<bfordGraph->vertexs[route.front()].key;
route.pop_front();
}
cout<<" "<<weight<<endl;
}
}
int main()
{
char vertex[] = {'S','T','X','Y','Z'};
int vernum = 5;
char adj[][2] = {{'S','T'},{'S','Y'},{'T','X'},{'T','Y'},{'T','Z'},{'X','T'},{'Y','X'},{'Y','Z'},{'Z','S'},{'Z','X'}};
int weight[] = {6,7,5,8,-4,-2,-3,9,2,7};
int adjnum = 10;
MSWBellmanFord *bellford = new MSWBellmanFord(vertex,vernum,adj,weight,adjnum);
bellford->BellmanMSW('S');
bellford->BellmanOutput();
return 0;
}
#include<iostream>
#include<list>
using namespace std;
#define MAXVALUE 10000 //定義一個最長路徑
//此處Prim算法的圖為有向圖
struct Edge
{
int verno; //鄰接數組中節點編號
int weight; //權值
Edge* next; //指向下一條邊
};
struct Vertex
{
Edge *adj; //所指向的節點所在邊
int verno; //鄰接數組中節點編號
char key; //關鍵字
};
struct Graph
{
Vertex *vertexs; //節點數組
int vertexnum; //節點個數
int adjnum; //邊數
};
class MSWBellmanFord
{
public:
MSWBellmanFord(char *vertex,int vernum,char adj[][2],int *weight,int adjnum);
void BellmanInsert(int source,int dest,int weight);
int BellmanFindKey(char key);
void BellmanInitSingleSource();
bool BellmanMSW(char sourceKey);
void BellmanOutput();
private:
int *swayweight;
int *parent;
Graph *bfordGraph;
};
MSWBellmanFord::MSWBellmanFord(char *vertex,int vernum,char adj[][2],int *weight,int adjnum)
{
int i,source,dest;
swayweight = new int[vernum];
parent = new int[vernum];
bfordGraph = new Graph;
bfordGraph->vertexs = new Vertex[vernum];
bfordGraph->adjnum = adjnum;
bfordGraph->vertexnum = vernum;
for(i = 0;i < vernum;i++)
{
bfordGraph->vertexs[i].key = vertex[i];
bfordGraph->vertexs[i].verno = i;
bfordGraph->vertexs[i].adj = NULL;
}
for(i = 0;i < adjnum;i++)
{
source = BellmanFindKey(adj[i][0]);
dest = BellmanFindKey(adj[i][1]);
BellmanInsert(source,dest,weight[i]);
//BellmanInsert(dest,source,weight[i]); //無向圖與有向圖的區別在此
}
}
void MSWBellmanFord::BellmanInsert(int source,int dest,int weight)
{
if(bfordGraph->vertexs[source].adj == NULL || bfordGraph->vertexs[source].adj->weight > weight)
{
Edge* newnode = new Edge;
newnode->verno = dest;
newnode->weight = weight;
newnode->next = bfordGraph->vertexs[source].adj;
bfordGraph->vertexs[source].adj = newnode;
}
else
{
Edge* temp = bfordGraph->vertexs[source].adj;
while(temp->next != NULL) //插入新邊的時候,把權值從低到高進行排序
{
if(temp->next->weight > weight)
break;
temp = temp->next;
}
Edge* newnode = new Edge;
newnode->verno = dest;
newnode->weight = weight;
newnode->next = temp->next;
temp->next = newnode;
}
}
int MSWBellmanFord::BellmanFindKey(char key)
{
int i;
for(i = 0;i < bfordGraph->vertexnum;i++)
{
if(bfordGraph->vertexs[i].key == key)
break;
}
return i;
}
void MSWBellmanFord::BellmanInitSingleSource()
{
int vernum = bfordGraph->vertexnum;
for(int i = 0;i < vernum;i++)
{
swayweight[i] = MAXVALUE;
parent[i] = i;
}
}
bool MSWBellmanFord::BellmanMSW(char sourceKey)
{
int location = BellmanFindKey(sourceKey);
int vernum = bfordGraph->vertexnum;
int i,j;
Edge *temp;
BellmanInitSingleSource();
//swayweight[0] = 0; //這裡為了偷懶,沒有隨意指定source,location本來是代表source的下標的
swayweight[location] = 0;
for(i = 0;i < vernum; i++)
{
/*
for(j = 0;j < vernum; j++)
{
temp = bfordGraph->vertexs[j].adj;
while(temp != NULL)
{
if((temp->weight + swayweight[j]) < swayweight[temp->verno])
{
swayweight[temp->verno] = temp->weight + swayweight[j];
parent[temp->verno] = j;
}
temp = temp->next;
}
}
*/
temp = bfordGraph->vertexs[location].adj;
while(temp != NULL)
{
if((temp->weight + swayweight[location]) < swayweight[temp->verno])
{
swayweight[temp->verno] = temp->weight + swayweight[location];
parent[temp->verno] = location;
}
temp = temp->next;
}
j = (location + 1) % vernum;
while(j != location)
{
temp = bfordGraph->vertexs[j].adj;
while(temp != NULL)
{
if((temp->weight + swayweight[j]) < swayweight[temp->verno])
{
swayweight[temp->verno] = temp->weight + swayweight[j];
parent[temp->verno] = j;
}
temp = temp->next;
}
j = (j + 1) % vernum;
}
}
for(j = 0;j < vernum; j++)
{
temp = bfordGraph->vertexs[j].adj;
while(temp != NULL)
{
if((temp->weight + swayweight[j]) < swayweight[temp->verno])
{
return false;
}
temp = temp->next;
}
}
return true;
}
void MSWBellmanFord::BellmanOutput()
{
int i,j,weight;
list<int> route;
cout<<"All the most shortest route from source : "<<endl;
for(i = 0;i < bfordGraph->vertexnum;i++)
{
j = i;
weight = swayweight[j];
do
{
route.push_front(j);
j = parent[j];
}while(parent[j] != j);
cout<<bfordGraph->vertexs[j].key;
cout<<"---"<<bfordGraph->vertexs[route.front()].key;
route.pop_front();
while(!route.empty())
{
if(route.front() != j)
cout<<"---"<<bfordGraph->vertexs[route.front()].key;
route.pop_front();
}
cout<<" "<<weight<<endl;
}
}
int main()
{
char vertex[] = {'S','T','X','Y','Z'};
int vernum = 5;
char adj[][2] = {{'S','T'},{'S','Y'},{'T','X'},{'T','Y'},{'T','Z'},{'X','T'},{'Y','X'},{'Y','Z'},{'Z','S'},{'Z','X'}};
int weight[] = {6,7,5,8,-4,-2,-3,9,2,7};
int adjnum = 10;
MSWBellmanFord *bellford = new MSWBellmanFord(vertex,vernum,adj,weight,adjnum);
bellford->BellmanMSW('S');
bellford->BellmanOutput();
return 0;
}
結果如下:
[cpp]
All the most shortest route from source :
S---S 0
S---Y---X---T 2
S---Y---X 4
S---Y 7
S---Y---X---T---Z -2
請按任意鍵繼續. . .
All the most shortest route from source :
S---S 0
S---Y---X---T 2
S---Y---X 4
S---Y 7
S---Y---X---T---Z -2
請按任意鍵繼續. . .