Question：
Implement int sqrt(int x).
Compute and return the square root of x.
Anwser 1： 二分法
[cpp]
class Solution {
public:
int sqrt(int x) {
if(x < 0) return -1; // assert(x >= 0);
long long x2 = (long long)x;
long long left = 0;
long long right = x2;
long long mid = 0;
while(left <= right){
mid = left + (right - left) / 2;
if(mid * mid == x2 || (mid * mid < x2 && (mid + 1) * (mid + 1) > x2)){
return (int)mid;
} else if(mid * mid < x2){
left = mid + 1;
} else{
right = mid - 1;
}
}
}
};
注意點：
1） 非負數判斷，負數沒有開平方根
2） 取值范圍，mid = left + (right - left) / 2; 可能會超過int最大取值范圍，因此需設mid類型為long long（C++沒ulong）
Anwser 2： 牛頓迭代法
[cpp]
class Solution {
public:
int sqrt(int x) {
if(x < 0) return -1; // assert(x >= 0);
double n = x;
while(abs(n * n - x) > 0.0001){
n = (n + x / n) / 2;
}
return (int)n;
}
};
注意點：
求a的平方根問題，可以轉化為x^2 - a = 0 求x值，進而 abc(x^2 -a) < 0.0001 （0.0001為接近精度）
令 f(x) = x^2 - a， f(x) 即是精度取值范圍（無限趨近於0）
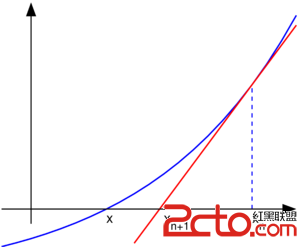對 函數 f(x) 求導：
變換公式，得：
把 f(x) = x^2 - a 公式求導，導入得： Xn+1 = Xn - (Xn^2 - a) / (2Xn) = Xn - (Xn - a/Xn) / 2 = (Xn + a/Xn) / 2
其中， Xn+1 無限接近於 Xn， 即有： Xn = (Xn + a/Xn) / 2
Anwser 3： 火星人算法
[cpp]
#include <stdio.h>
int InvSqrt(int x)
{
float x2 = (float)x;
float xhalf = x2 / 2;
int i = *(int*) & x2; // get bits for floating VALUE
i = 0x5f375a86 - (i>>1); // gives initial guess y0
x2 = *(float*) & i; // convert bits BACK to float
x2 = x2 * (1.5f - xhalf * x2 * x2); // Newton step, repeating increases accuracy
x2 = x2 * (1.5f - xhalf * x2 * x2); // Newton step, repeating increases accuracy
x2 = x2 * (1.5f - xhalf * x2 * x2); // Newton step, repeating increases accuracy
printf("\n\n1/x = %d\n", (int)(1/x2));
return (int)(1/x2);
}
int main(){
//InvSqrt(65535);
InvSqrt(10);
InvSqrt(2147395599);
InvSqrt(1297532724);
return 0;
}
說明：
此方法傳說非常高效，我是參考別人的float寫的int（參數）
