二叉樹 建立 非遞歸-前序-中序-後序-廣度優先遍歷

二叉樹是數據結構中非常基本 但是非常重要的一種
它是最小堆 二叉搜索樹  AVL樹  紅黑樹的基礎
對於二叉樹的各種操作必須完全理解透徹才行
[cpp]
#include <stdio.h>  
#include <stack>  
#include <queue>  
#include <stdlib.h>  
 
typedef int KeyType; 
 
//二叉樹節點  
typedef struct Node 
{ 
    KeyType key; 
    Node* lChild; 
    Node* rChild; 
}Node, *PNode; 
 
 
//建樹函數 此處采用了遞歸的方式建樹  
void createTree(PNode& root) 
{ 
    int temp; 
    scanf("%d", &temp); 
    //輸入0表示當前節點建立結束  
    if(temp == 0) 
    { 
        root = NULL; 
        return; 
    } 
    else 
    { 
        root = (PNode)malloc(sizeof(Node)); 
        root->key = temp;            //初始化當前節點  
        createTree(root->lChild);    //初始化當前節點左孩子  
        createTree(root->rChild);    //初始化當前節點右孩子  
    } 
} 
 
//前序遞歸遍歷  不做詳述  
void preOrder(PNode root) 
{ 
    if(!root) 
        return; 
    preOrder(root->lChild); 
    printf("%3d", root->key); 
    preOrder(root->rChild); 
} 
 
 
//前序非遞歸遍歷  
void preOrderNonRecursive(PNode root) 
{ 
    PNode p = root; 
    stack<PNode> node_stack;//采用棧作為輔助結構  
    while(p || !node_stack.empty()) 
    { 
        //定位到當前節點的最左節點（注意：此處最左節點也被放入了棧中）  
        while(p) 
        { 
            node_stack.push(p); 
            p = p->lChild; 
        } 
        //定位到當前節點最左節點之後訪問之 然後訪問它的右子節點  
        if(!node_stack.empty()) 
        { 
            p = node_stack.top(); 
            node_stack.pop(); 
            printf("%3d", p->key); 
            p = p->rChild; 
        } 
    } 
} 
 
//中序遍歷  
void inOrder(PNode root) 
{ 
    if(!root) 
        return; 
    PNode p = root; 
    printf("%3d", p->key); 
    inOrder(p->lChild); 
    inOrder(p->rChild); 
} 
 
//中序非遞歸遍歷  
//很多人講中序非遞歸遍歷比前序和後序非遞歸遍歷要困難  
//個人以為這只是因為對前序和後序非遞歸遍歷的理解不夠透徹  
void inOrderNonRecursive(PNode root) 
{ 
    stack<PNode> node_stack; 
    PNode p = root; 
    while(p || !node_stack.empty()) 
    { 
        //沿左子樹挨個訪問根節點 一直到最左子節點 同時將他們放入棧中  
        //注意：在中序遍歷中，將節點放入棧中是為了回溯時可以定位到他們的右子節點，但是由於他們本身已經被訪問過，  
        //所以在彈出棧的時候只需要直接去處理他們的右子節點即可  
        while(p) 
        { 
            printf("%3d", p->key); 
            node_stack.push(p); 
            p = p->lChild; 
        } 
        if(!node_stack.empty()) 
        { 
            p = node_stack.top(); 
            node_stack.pop(); 
            p = p->rChild;    //如前所述，直接處理其右子節點  並不對棧中元素本身做處理  
        } 
    } 
} 
 
//後序遞歸遍歷  
void postOrder(PNode root) 
{ 
    if(!root) 
        return; 
    PNode p = root; 
    postOrder(p->rChild); 
    printf("%3d", p->key); 
    postOrder(p->lChild); 
} 
 
 
//後序非遞歸遍歷  
//跟前序遍歷一個道理 此處不作贅述  
void postOrderNonRecursive(PNode root) 
{ 
    stack<PNode> node_stack; 
    PNode p = root; 
    while(p || !node_stack.empty()) 
    { 
        while(p) 
        { 
            node_stack.push(p); 
            p = p->rChild; 
        } 
        if(!node_stack.empty()) 
        { 
            p = node_stack.top(); 
            node_stack.pop(); 
            printf("%3d", p->key); 
            p = p->lChild; 
        } 
    } 
} 
 
//深度優先遍歷  
//深度優先遍歷的思想就是先將根節點放入隊列，然後對隊列中的每個節點，訪問完頭部節點之後，彈出頭節點，  
//同時將頭結點的左子節點和右子節點放入隊列，如此循環即可  
void depthFirst(PNode root) 
{ 
    if(!root) 
        return; 
    queue<PNode> node_queue; 
    PNode p = root; 
    node_queue.push(p); 
    while(!node_queue.empty()) 
    { 
        p = node_queue.front(); 
        printf("%3d", p->key); 
        node_queue.pop(); 
        if(p->lChild) 
            node_queue.push(p->lChild); 
        if(p->rChild) 
            node_queue.push(p->rChild); 
    } 
} 
 
int main() 
{ 
    PNode root = NULL; 
    createTree(root); 
     
    printf("pre order               :"); 
    preOrder(root); 
    printf("\n"); 
     
    printf("pre nonrecursive order  :"); 
    preOrderNonRecursive(root); 
    printf("\n"); 
     
    printf("in order                :"); 
    inOrder(root); 
    printf("\n"); 
     
    printf("in nonrecursive order   :"); 
    inOrderNonRecursive(root); 
    printf("\n"); 
     
    printf("post order              :"); 
    postOrder(root); 
    printf("\n"); 
     
    printf("post nonrecursive order :"); 
    postOrderNonRecursive(root); 
    printf("\n"); 
     
    printf("depth first order       :"); 
    depthFirst(root); 
    printf("\n"); 
    return 0; 
} 

#include <stdio.h>
#include <stack>
#include <queue>
#include <stdlib.h>

typedef int KeyType;

//二叉樹節點
typedef struct Node
{
 KeyType key;
 Node* lChild;
 Node* rChild;
}Node, *PNode;

//建樹函數 此處采用了遞歸的方式建樹
void createTree(PNode& root)
{
 int temp;
 scanf("%d", &temp);
 //輸入0表示當前節點建立結束
 if(temp == 0)
 {
  root = NULL;
  return;
 }
 else
 {
  root = (PNode)malloc(sizeof(Node));
  root->key = temp;   //初始化當前節點
  createTree(root->lChild); //初始化當前節點左孩子
  createTree(root->rChild); //初始化當前節點右孩子
 }
}

//前序遞歸遍歷  不做詳述
void preOrder(PNode root)
{
 if(!root)
  return;
 preOrder(root->lChild);
 printf("%3d", root->key);
 preOrder(root->rChild);
}

//前序非遞歸遍歷
void preOrderNonRecursive(PNode root)
{
 PNode p = root;
 stack<PNode> node_stack;//采用棧作為輔助結構
 while(p || !node_stack.empty())
 {
  //定位到當前節點的最左節點（注意：此處最左節點也被放入了棧中）
  while(p)
  {
   node_stack.push(p);
   p = p->lChild;
  }
  //定位到當前節點最左節點之後訪問之 然後訪問它的右子節點
  if(!node_stack.empty())
  {
   p = node_stack.top();
   node_stack.pop();
   printf("%3d", p->key);
   p = p->rChild;
  }
 }
}

//中序遍歷
void inOrder(PNode root)
{
 if(!root)
  return;
 PNode p = root;
 printf("%3d", p->key);
 inOrder(p->lChild);
 inOrder(p->rChild);
}

//中序非遞歸遍歷
//很多人講中序非遞歸遍歷比前序和後序非遞歸遍歷要困難
//個人以為這只是因為對前序和後序非遞歸遍歷的理解不夠透徹
void inOrderNonRecursive(PNode root)
{
 stack<PNode> node_stack;
 PNode p = root;
 while(p || !node_stack.empty())
 {
  //沿左子樹挨個訪問根節點 一直到最左子節點 同時將他們放入棧中
  //注意：在中序遍歷中，將節點放入棧中是為了回溯時可以定位到他們的右子節點，但是由於他們本身已經被訪問過，
  //所以在彈出棧的時候只需要直接去處理他們的右子節點即可
  while(p)
  {
   printf("%3d", p->key);
   node_stack.push(p);
   p = p->lChild;
  }
  if(!node_stack.empty())
  {
   p = node_stack.top();
   node_stack.pop();
   p = p->rChild;    //如前所述，直接處理其右子節點  並不對棧中元素本身做處理
  }
 }
}

//後序遞歸遍歷
void postOrder(PNode root)
{
 if(!root)
  return;
 PNode p = root;
 postOrder(p->rChild);
 printf("%3d", p->key);
 postOrder(p->lChild);
}

//後序非遞歸遍歷
//跟前序遍歷一個道理 此處不作贅述
void postOrderNonRecursive(PNode root)
{
 stack<PNode> node_stack;
 PNode p = root;
 while(p || !node_stack.empty())
 {
  while(p)
  {
   node_stack.push(p);
   p = p->rChild;
  }
  if(!node_stack.empty())
  {
   p = node_stack.top();
   node_stack.pop();
   printf("%3d", p->key);
   p = p->lChild;
  }
 }
}

//深度優先遍歷
//深度優先遍歷的思想就是先將根節點放入隊列，然後對隊列中的每個節點，訪問完頭部節點之後，彈出頭節點，
//同時將頭結點的左子節點和右子節點放入隊列，如此循環即可
void depthFirst(PNode root)
{
 if(!root)
  return;
 queue<PNode> node_queue;
 PNode p = root;
 node_queue.push(p);
 while(!node_queue.empty())
 {
  p = node_queue.front();
  printf("%3d", p->key);
  node_queue.pop();
  if(p->lChild)
   node_queue.push(p->lChild);
  if(p->rChild)
   node_queue.push(p->rChild);
 }
}

int main()
{
 PNode root = NULL;
 createTree(root);
 
 printf("pre order               :");
 preOrder(root);
 printf("\n");
 
 printf("pre nonrecursive order  :");
 preOrderNonRecursive(root);
 printf("\n");
 
 printf("in order                :");
 inOrder(root);
 printf("\n");
 
 printf("in nonrecursive order   :");
 inOrderNonRecursive(root);
 printf("\n");
 
 printf("post order              :");
 postOrder(root);
 printf("\n");
 
 printf("post nonrecursive order :");
 postOrderNonRecursive(root);
 printf("\n");
 
 printf("depth first order       :");
 depthFirst(root);
 printf("\n");
 return 0;
}

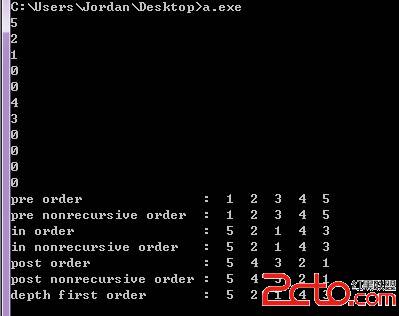
運行截圖：