概述
假如你有一張地圖,地圖上給出了每一對相鄰城市的距離,從一個地點到另一個地點,如何找到一條最短的路?最短路算法要解決的就是這類問題。定義:給定一個有(無)向圖,每一條邊有一個權值w,給定一個起始點S和終止點T,求從S出發走到T的權值最小路徑,即為最短路徑。最短路徑算法依賴一種性質:一條兩頂點間的最短路徑包含路徑上其他最短路徑。最簡單的說就是:最短路徑的子路徑是最短路徑。
松弛技術
松弛技術本質上是一個貪心操作。松弛操作:對每個頂點v屬於V,都設置一個屬性d[v],用來描述從源點s到v的最短路徑上權值的上界,稱為最短路徑估計(shortest-path estimate),同時parent[v]代表前趨。初始化偽代碼:
[html]
INITIALIZE-SINGLE-SOURCE(G, s)
for each vertex v (- V[G]
do
d[v] <- INF
parent[v] <- NULL
done
d[s] <- 0
INITIALIZE-SINGLE-SOURCE(G, s)
for each vertex v (- V[G]
do
d[v] <- INF
parent[v] <- NULL
done
d[s] <- 0
初始化後,對所有v屬於V,parent[v] = NULL,對v屬於{V - {s}},有d[s] = 0 以及d[v]=無窮。松弛一條邊(u, v),如果這條邊可以對最短路徑改進,則更新d[v]和parent[v]。一次松弛操作可以減少最短路徑估計的值d[v],並更新v的前趨域parent[v].下面的偽代碼對邊(u, v)進行了一步松弛操作:
[html]
RELAX(u, v, w)
if d[v] > d[u] + w(u, v)
then
d[v] <- d[u] + w(u, v)
parent[v] <- u
fi
RELAX(u, v, w)
if d[v] > d[u] + w(u, v)
then
d[v] <- d[u] + w(u, v)
parent[v] <- u
fi
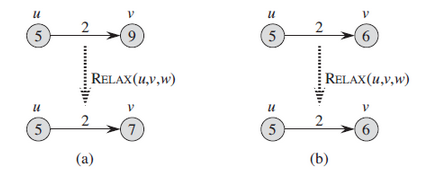
上圖所示中,左邊例子,最短路徑估計值減小,右邊例子,最短路徑估計值不變。當發現v到u有更近的路徑時,更新d[v]和parent[v]
Dijkstra算法
解決最短路徑問題,最經典的算法是Dijkstra算法,它是一種單源最短路徑算法,其核心思想是貪心算法(Greedy Algorithm)。Dijkstra算法要求所有邊的權值非負
算法思想
設G = (V, E)是一個帶權有向圖,把圖中頂點集合V分成兩組,第一組為已求出最短路徑的頂點集合(用S表示,初始時S中只有一個源點,以後每求得一條最短路徑,就將其加入到集合S中,直到全部頂點都加入到S中,算法就結束了);第二組為其余未確定最短路徑的頂點集合(用U表示),按最短路徑長度的遞增次序把第二組的頂點加入S中。在加入的過程中,總保持從源點v到S中各頂點的最短路徑長度不大於從源點v到U中任何頂點的最短路徑長度。此外,每個頂點對應一個距離,S中的頂點的距離就是從v到此頂點的最短路徑長度,U中的頂點的距離,是從v到此頂點只包括S中的頂點為中間頂點的當前最短路徑長度
偽代碼
[html]
Dijkstra(G, w, s)
INITIALIZE-SINGLE-SOURCE(G, s)
S <- 空集
Q <- V[G]
while Q != 空集
do
u <- EXTRACT-MIN(Q)
S <- S && {u}
for each vertex v (- Adj[u]
do
RELAX(u, v, w)
done
done
Dijkstra(G, w, s)
INITIALIZE-SINGLE-SOURCE(G, s)
S <- 空集
Q <- V[G]
while Q != 空集
do
u <- EXTRACT-MIN(Q)
S <- S && {u}
for each vertex v (- Adj[u]
do
RELAX(u, v, w)
done
done
Dijkstra算法時間主要消耗在尋找最小權值的邊,和松弛所有剩余邊,所以EXTRACT-MIN(Q)這一步,更好的方法是使用優先隊列,優先隊列可以使用二叉堆
算法描述
假設用帶權的鄰接矩陣arcs來表示帶權有向圖,arcs[i][j]表示弧<vi, vj>上的權值。若<vi, vj>不存在,則置arcs[i][j]為無窮(在計算機上可用允許的最大值代替)。S為已找到從v出發的最短路徑的終點的集合,它的初始狀態為空集。那麼,從v出發到圖上其余各頂點(終點)vi可能達到的最短路徑長度的初值為:D[I] = arcs[src][i] vi (- V
選擇vj,使得D[j] = Min{D[i] | vi (- V - S},vj就是當前求得的一條從v出發的最短路徑的終點。令S = S && {j}
修改從v出發到集合V - S上任一頂點vk可達的最短路徑長度。如果 D[j] + arcs[j][k] < D[k],則修改D[k] = D[j] + arcs[j][k]
重復操作2、3共n-1次。由此求得從v到圖中其余各頂點的最短路徑長度是依路徑長度遞增的序列
實現代碼(c語言)
[cpp]
#include <stdio.h>
#include <stdlib.h>
// 圖頂點的最大值
#define NODE 102
// 邊權值的最大值
#define MAX 10002
// 鄰接矩陣存儲圖
int map[NODE][NODE];
// 記錄src到其它各個頂點的最短路徑長度
int dis[NODE];
// 標記數組,判斷哪些src到哪些頂點的最短路徑已經求出
int mark[NODE];
/**
* 用Dijkstra算法求圖map的src到其余頂點的最短路徑
* src為單源頂點,n為圖中頂點個數
*/
void dijkstra(int src, int n)
{
int i, j, min, k, tmp;
// 初始化
for (i = 0; i < n; i ++) {
dis[i] = map[src][i];
mark[i] = 0;
}
dis[src] = 0;
mark[src] = 1;
// n-1次主循環,每次循環求得src到某個頂點v的最短路徑
for (i = 1; i < n; i ++) {
min = MAX;
k = src;
for (j = 0; j < n; j ++) {
if (!mark[j] && dis[j] < min) {
k = j;
min = dis[j];
}
}
mark[k] = 1;
// 更新src到其它各頂點的最短路徑
for (j = 0; j < n; j ++) {
tmp = map[k][j] + dis[k];
if (tmp < dis[j] && mark[j] == 0) {
dis[j] = tmp;
}
}
}
}
#include <stdio.h>
#include <stdlib.h>
// 圖頂點的最大值
#define NODE 102
// 邊權值的最大值
#define MAX 10002
// 鄰接矩陣存儲圖
int map[NODE][NODE];
// 記錄src到其它各個頂點的最短路徑長度
int dis[NODE];
// 標記數組,判斷哪些src到哪些頂點的最短路徑已經求出
int mark[NODE];
/**
* 用Dijkstra算法求圖map的src到其余頂點的最短路徑
* src為單源頂點,n為圖中頂點個數
*/
void dijkstra(int src, int n)
{
int i, j, min, k, tmp;
// 初始化
for (i = 0; i < n; i ++) {
dis[i] = map[src][i];
mark[i] = 0;
}
dis[src] = 0;
mark[src] = 1;
// n-1次主循環,每次循環求得src到某個頂點v的最短路徑
for (i = 1; i < n; i ++) {
min = MAX;
k = src;
for (j = 0; j < n; j ++) {
if (!mark[j] && dis[j] < min) {
k = j;
min = dis[j];
}
}
mark[k] = 1;
// 更新src到其它各頂點的最短路徑
for (j = 0; j < n; j ++) {
tmp = map[k][j] + dis[k];
if (tmp < dis[j] && mark[j] == 0) {
dis[j] = tmp;
}
}
}
}