彼岸
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 2279 Accepted Submission(s): 1256
Problem Description
突破蝙蝠的包圍,yifenfei來到一處懸崖面前,懸崖彼岸就是前進的方向,好在現在的yifenfei已經學過御劍術,可御劍輕松飛過懸崖。
現在的問題是:懸崖中間飛著很多紅,黃,藍三種顏色的珠子,假設我們把懸崖看成一條長度為n的線段,線段上的每一單位長度空間都可能飛過紅,黃,藍三種珠子,而yifenfei必定會在該空間上碰到一種顏色的珠子。如果在連續3段單位空間碰到的珠子顏色都不一樣,則yifenfei就會墜落。
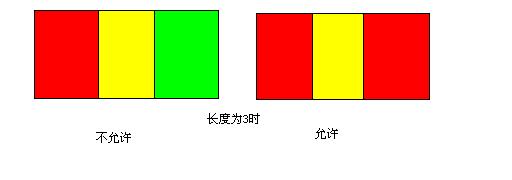
比如經過長度為3的懸崖,碰到的珠子先後為 “紅黃藍”,或者 “藍紅黃” 等類似情況就會墜落,而如果是 “紅黃紅” 或者 “紅黃黃”等情況則可以安全到達。
現在請問:yifenfei安然抵達彼岸的方法有多少種?

Input
輸入數據首先給出一個整數C,表示測試組數。
然後是C組數據,每組包含一個正整數n (n<40)。
Output
對應每組輸入數據,請輸出一個整數,表示yifenfei安然抵達彼岸的方法數。
每組輸出占一行。
Sample Input
2
2
3
Sample Output
9
21
Author
yifenfei
Source
ACM程序設計期末考試081230
Recommend
yifenfei
算的上是自己第一道自己解決的dp題目了 對dp都絕望了
思路:
用 dp[n][a][b] n代表長度 a代表n-1位置處的顏色 b代表n位置處的顏色
則有
dp[n][a][b]=dp[n-1][a][a]+dp[n-1][b][a];
同理
dp[n][a][a]=dp[n-1][a][a]+dp[n-1][b][a]+dp[n-1][c][a];
dp[n][a][c]=dp[n-1][a][a]+dp[n-1][c][a];
[cpp]
#include<stdio.h>
#include<algorithm>
using namespace std;
int dp[100][3][3];
int main()
{
int cas,n,i,j,a,b,c;
dp[2][1][1]=dp[2][1][2]=dp[2][1][3]=1;
dp[2][2][1]=dp[2][2][2]=dp[2][2][3]=1;
dp[2][3][1]=dp[2][3][2]=dp[2][3][3]=1;
for(n=3;n<40;n++)
{
for(a=1;a<=3;a++)
for(b=1;b<=3;b++)
for(c=1;c<=3;c++)
{
if(a==b||b==c||a==c) continue;
dp[n][a][b]=dp[n-1][a][a]+dp[n-1][b][a];
dp[n][a][a]=dp[n-1][a][a]+dp[n-1][b][a]+dp[n-1][c][a];
dp[n][a][c]=dp[n-1][a][a]+dp[n-1][c][a];
}
}
scanf("%d",&cas);
while(cas--)
{
scanf("%d",&n);
int ans=0;
if(n==0) {printf("0\n");continue;}
else if(n==1) {printf("3\n");continue;}
ans=dp[n][1][1]+dp[n][1][2]+dp[n][1][3]
+dp[n][2][1]+dp[n][2][2]+dp[n][2][3]
+dp[n][3][1]+dp[n][3][2]+dp[n][3][3];
printf("%d\n",ans);
}
return 0;
}