POJ 1699 Best Sequence

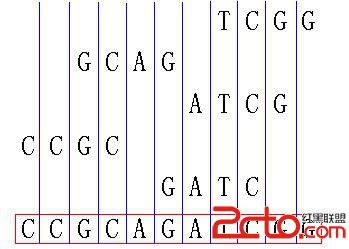
Best Sequence Time Limit: 1000MS   Memory Limit: 10000K  Total Submissions: 4198   Accepted: 1662    Description   The twenty-first century is a biology-technology developing century. One of the most attractive and challenging tasks is on the gene project, especially on gene sorting program. Recently we know that a gene is made of DNA. The nucleotide bases from which DNA is built are A(adenine), C(cytosine), G(guanine), and T(thymine). Given several segments of a gene, you are asked to make a shortest sequence from them. The sequence should use all the segments, and you cannot flip any of the segments.    For example, given 'TCGG', 'GCAG', 'CCGC', 'GATC' and 'ATCG', you can slide the segments in the following way and get a sequence of length 11. It is the shortest sequence (but may be not the only one).   

    Input   The first line is an integer T (1 <= T <= 20), which shows the number of the cases. Then T test cases follow. The first line of every test case contains an integer N (1 <= N <= 10), which represents the number of segments. The following N lines express N segments, respectively. Assuming that the length of any segment is between 1 and 20. Output   For each test case, print a line containing the length of the shortest sequence that can be made from these segments. Sample Input   1 5 TCGG GCAG CCGC GATC ATCG Sample Output   11Source   POJ Monthly--2004.07.18 [Submit] [Go Back] [Status] [Discuss]    Home Page Go Back To top       思路：把完全包含在一個串中的另一個串去掉。然後預處理出各個串的銜接位置。最後在dfs全排列，找出最小答案

#include <iostream>
#include <cstring>
#include <cstdio>
#include <cstdlib>
#define INF 0x7ffffff
using namespace std;
char s1[20][30],s2[20][30];
int len[20],pos[20][20],pt[20];
bool status[20];
int n,Min;
int main()
{
    //freopen("data1.in","r",stdin);
    bool check(char str1[30],char str2[30]);
    void dfs(int k);
    int t;
    scanf("%d",&t);
    while(t--)
    {
        int Top=0;
        scanf("%d",&n);
        for(int i=0;i<=n-1;i++)
        {
            scanf("%s",s2[i]);
        }
        for(int i=0;i<=n-1;i++)
        {
            int j;
            for(j=i+1;j<=n-1;j++)
            {
                int l1,l2;
                l1 = strlen(s2[i]);
                l2 = strlen(s2[j]);
                if(l1==l2&&strcmp(s2[i],s2[j])==0)
                {
                    break;
                }else if(l1<l2&&check(s2[i],s2[j]))
                {
                    break;
                }
            }
            if(j==n)
            {
                strcpy(s1[Top++],s2[i]);
            }
        }
        n=Top;
        for(int i=0;i<=n-1;i++)
        {
            len[i] = strlen(s1[i]);
        }
        for(int i=0;i<=n-1;i++)
        {
            for(int j=0;j<=n-1;j++)
            {
                if(i==j)
                {
                    continue;
                }
                int x;
                for(x=0;x<=len[i]-1;x++)
                {
                    int y;
                    for(y = x;y<=len[i]-1;y++)
                    {
                        if(s1[i][y] != s1[j][y-x])
                        {
                            break;
                        }
                    }
                    if(y==len[i])
                    {
                        break;
                    }
                }
                pos[i][j] = x;
            }
        }
        memset(status,false,sizeof(status));
        Min=INF;
        dfs(0);
        printf("%d\n",Min);
    }
    return 0;
}
//str1是否在str2中
bool check(char str1[30],char str2[30])
{
    int l1 = strlen(str1);
    int l2 = strlen(str2);
    int i,j;
    for(i=0;i<=l2-1;i++)
    {
        for(j=i;j-i<=l1-1;j++)
        {
            if(str2[j]!=str1[j-i])
            {
                break;
            }
        }
        if(j-i==l1)
        {
            return true;
        }
    }
    return false;
}
void dfs(int k)
{
    for(int i=0;i<=n-1;i++)
    {
        if(!status[i])
        {
            pt[k] = i;
            status[i] = true;
            if(k==n-1)
            {
                int s = len[pt[0]];
                for(int j=1;j<=n-1;j++)
                {
                    int sum1 = len[pt[j]] - (len[pt[j-1]]-pos[pt[j-1]][pt[j]]);
                    s+=sum1;
                }
                Min=min(Min,s);
            }else
            {
                dfs(k+1);
            }
            status[i] = false;
        }
    }
}