HDU 2196 Computer - from lanshui_Yang

Problem Description
A school bought the first computer some time ago(so this computer's id is 1). During the recent years the school bought N-1 new computers. Each new computer was connected to one of settled earlier. Managers of school are anxious about slow functioning of the net and want to know the maximum distance Si for which i-th computer needs to send signal (i.e. length of cable to the most distant computer). You need to provide this information.

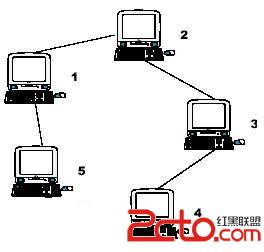
Hint: the example input is corresponding to this graph. And from the graph, you can see that the computer 4 is farthest one from 1, so S1 = 3. Computer 4 and 5 are the farthest ones from 2, so S2 = 2. Computer 5 is the farthest one from 3, so S3 = 3. we also get S4 = 4, S5 = 4.

Input
Input file contains multiple test cases.In each case there is natural number N (N<=10000) in the first line, followed by (N-1) lines with descriptions of computers. i-th line contains two natural numbers - number of computer, to which i-th computer is connected and length of cable used for connection. Total length of cable does not exceed 10^9. Numbers in lines of input are separated by a space.

Output
For each case output N lines. i-th line must contain number Si for i-th computer (1<=i<=N).

Sample Input
5
1 1
2 1
3 1
1 1

Sample Output
3
2
3
4
4    題目大意:抽象以後的問題很容易理解：給你一棵樹，讓你求出樹中任意一個節點到其他節點的最大距離。    解題思路：簡單的想法是對每個節點都調用一次bfs來求和樹中其他節點的距離的最大值，但是，這顯然會TLE。換種思路，先求出樹的直徑的兩個端點A 和 B ， 那麼樹中任意一個節點C 在樹中距離其他節點的最大值一定是max{A -> C  ， B -> C} ,這樣，只需調用3次 bfs 就可以了，第一次以任意節點為起點進行bfs找端點A ， 第二次是以端點A為起點進行 bfs 找端點B（此過程中同時求出了樹中其他節點到端點A的距離的值 ） ， 第三次是以端點B為起點進行bfs ， 此過程是為了求出樹中其他節點到端點 B 的距離的值 同時 求出max{A -> C  ， B -> C} 。    下面請看代碼：

#include<iostream>
#include<cstring>
#include<string>
#include<algorithm>
#include<cstdio>
#include<queue>
using namespace std ;
const int MAXN = 1e6 +7 ;
int n ;
struct Node
{
    int adj ;
    int dist ;
    Node *next ;
};
Node *vert[MAXN] ;
int vis[MAXN] ; // 建立標記數組
int distmp[MAXN] ;   // 記錄端點A到樹中其他節點的距離
int disans[MAXN] ;  // 記錄 max{A -> C  ， B -> C}
queue<int> q ;
int bfs(int start)
{
    memset(vis , 0 , sizeof(vis)) ;  // 每次 bfs 都別忘記
    memset(distmp , 0 , sizeof(distmp)) ;
    while (!q.empty())
    {
        q.pop() ;
    }
    int duan ;
    vis[start] = 1 ;
    distmp[start] = 0 ;
    if(distmp[start] > disans[start])  // 找max{A -> C  ， B -> C}
    {
        disans[start] = distmp[start] ;
    }
    q.push(start) ;
    int maxr = 0 ;
    Node * p ;
    int tmp ;
    while (!q.empty())
    {
        tmp = q.front() ;
        q.pop() ;
        vis[tmp] = 1 ;
        p = vert[tmp] ;
        while (p != NULL)
        {
            int tp2 = p -> adj ;
            if(!vis[tp2])
            {
                vis[tp2] = 1 ;
                distmp[tp2] = distmp[tmp] + p -> dist ;
                if(distmp[tp2] > disans[tp2])
                {
                    disans[tp2] = distmp[tp2] ;
                }
                if(maxr < distmp[tp2])
                {
                    duan = tp2 ;
                    maxr = distmp[tp2] ;
                }
                q.push(tp2) ;
            }
            p = p -> next ;
        }
    }
    return duan ;
}
void ans()  // 進行3次bfs
{
    int duan1 = bfs(1) ;
    int duan2 = bfs(duan1) ;
    bfs(duan2) ;
}
int main()
{
    while (scanf("%d" , &n) != EOF)
    {
        memset(disans , 0 , sizeof(disans)) ;
        memset(vert , 0 , sizeof(vert)) ;
        int i ;
        getchar() ;
        for(i = 2 ; i <= n ; i ++)  // 建圖 ，此處很關鍵，千萬要理解題意！！
        {
            int b , d ;
            scanf("%d%d" , &b , &d) ;
            Node *p ;
            p = new Node ;
            p -> adj = b ;
            p -> dist = d ;
            p -> next = vert[i] ;
            vert[i] = p ;

            p = new Node ;
            p -> adj = i ;
            p -> dist = d ;
            p ->next = vert[b] ;
            vert[b] = p ;
        }
        ans() ;
        for(i = 1 ; i <= n ; i ++)
        {
            printf("%d\n" , disans[i]) ;
        }
    }
    return 0 ;
}