How Many Points of Intersection?
We have two rows. There are a dots on the top row and b dots on the bottom row. We draw line segments connecting every dot on the top row with every dot on the bottom row. The dots are arranged in such a way that the number of internal intersections among the line segments is maximized. To achieve this goal we must not allow more than two line segments to intersect in a point. The intersection points on the top row and the bottom are not included in our count; we can allow more than two line segments to intersect on those two rows. Given the value of a and b, your task is to compute P(a, b), the number of intersections in between the two rows. For example, in the following figure a = 2 and b = 3. This figure illustrates that P(2, 3) = 3.
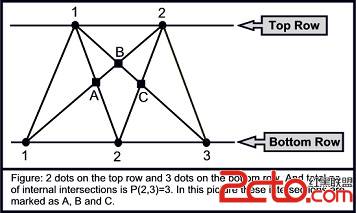
Input
Each line in the input will contain two positive integers a ( 0 < a20000) and b ( 0 < b20000). Input is terminated by a line where both a and b are zero. This case should not be processed. You will need to process at most 1200 sets of inputs.
Output
For each line of input, print in a line the serial of output followed by the value of P(a, b). Look at the output for sample input for details. You can assume that the output for the test cases will fit in 64-bit signed integers.
Sample Input
2 2
2 3
3 3
0 0
Sample Output
Case 1: 1
Case 2: 3
Case 3: 9
有兩條線,輸入第一條線上點n個,和第二條線上點m個。 輸出如果把n,m上每兩點都相連,交點有幾個。。
解法:加入n有3個,m有3個。假設從m這條線找點去連接m, 第一點連過去3條一個交點都沒。第二點連過去。m2連n1的時候將會交第一點連過去的m1n2、m1n3,m2連n2的時候將會交第一點和第二點連過去的m1n3。。為1 + 2;第三點連過去將會交第一點和第二點連過去的幾條。為 2 * (1 + 2)。。
找到規律可以推出。。交點個數x為,求出一個sum = (1 + 2 + ... + n - 1)。 然後x = sum * 1 + sum * 2 + ... + m - 1;
輸出x。
代碼:
#include <stdio.h>
#include <string.h>
int a, b;
int main()
{
int t = 1;
while (scanf("%d%d", &a, &b) != EOF && a || b)
{
long long num1 = 0;
long long sum = 0;
for (int i = 1; i < a; i ++)
num1 += i;
for (int i = 1; i < b; i ++)
sum += num1 * i;
printf("Case %d: %lld\n", t ++, sum);
}
return 0;
}