Slash Maze
By filling a rectangle with slashes (/) and backslashes ( ), you can generate nice little mazes. Here is an example:
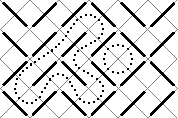
As you can see, paths in the maze cannot branch, so the whole maze only contains cyclic paths and paths entering somewhere and leaving somewhere else. We are only interested in the cycles. In our example, there are two of them.
Your task is to write a program that counts the cycles and finds the length of the longest one. The length is defined as the number of small squares the cycle consists of (the ones bordered by gray lines in the picture). In this example, the long cycle has length 16 and the short one length 4.
Input
The input contains several maze descriptions. Each description begins with one line containing two integers w and h ( ), the width and the height of the maze. The next h lines represent the maze itself, and contain w characters each; all these characters will be either ``/" or ``\".
The input is terminated by a test case beginning with w = h = 0. This case should not be processed.
Output
For each maze, first output the line ``Maze #n:'', where n is the number of the maze. Then, output the line ``kCycles; the longest has length l.'', where k is the number of cycles in the maze and l the length of the longest of the cycles. If the maze does not contain any cycles, output the line ``There are no cycles.".
Output a blank line after each test case.
Sample Input
6 4
\//\\/
\///\/
//\\/\
\/\///
3 3
///
\//
\\\
0 0
Sample Output
Maze #1:
2 Cycles; the longest has length 16.
Maze #2:
There are no cycles.
題意:輸入'/'、'\'組合成一個迷宮。。要找出迷宮中可以形成回路的回路個數和回路中最長的回路長度。。。
思路:這裡用了2個方法。。。
第一個方法是: 把迷宮每一個格子轉換成3 *3的格子。。斜線的格子用1表示,其余用0表示,每個格子保存好後。在新的地圖進行搜索。這樣就可以廣搜BFS。如果地圖中為0點的點可以走出邊界。就是不可能形成回路。
如果不會走出邊界。就必然可以形成回路,每次搜完一點後,把相鄰的一片標記掉。就不用重復搜索了。如果搜索到可以形成回路的。他的長度為走過的格子數除以3。
#include <stdio.h>
#include <string.h>
int n, m;
int d[4][2] = {{-1, 0}, {0, 1}, {1, 0}, {0, -1}};
int map[275][275];
int maxx;
char sb;
struct Q
{
int x;
int y;
} q[66666];
int vis[275][275];
int numc;
void bfs(int x, int y)
{
memset(q, 0, sizeof(q));
memset(vis, 0, sizeof(vis));
int h = 0;
int r = 1;
int num = 1;
q[h].x = x;
q[h].y = y;
vis[x][y] = 1;
while (h < r)
{
for (int i = 0; i < 4; i ++)
{
int xx = q[h].x + d[i][0];
int yy = q[h].y + d[i][1];
if (xx < 0 || xx >= 3 * n || yy < 0 || yy >= 3 * m)
{
return;
}
if (map[xx][yy] == 0 && vis[xx][yy] == 0)
{
vis[xx][yy] = 1;
q[r].x = xx;
q[r].y = yy;
num ++;
r ++;
}
}
h ++;
}
numc ++;
if (maxx < num / 3)
maxx = num / 3;
}
void bfs2(int x, int y)
{
memset(q, 0, sizeof(q));
int h = 0;
int r = 1;
q[h].x = x;
q[h].y = y;
map[x][y] = 1;
while (h < r)
{
for (int i = 0; i < 4; i ++)
{
int xx = q[h].x + d[i][0];
int yy = q[h].y + d[i][1];
if (map[xx][yy] == 0 && xx >= 0 && xx < 3 * n && yy >= 0 && yy < 3 * m)
{
map[xx][yy] = 1;
q[r].x = xx;
q[r].y = yy;
r ++;
}
}
h ++;
}
}
int main()
{
int tt = 1;
while (scanf("%d%d", &m, &n) != EOF && n + m)
{
maxx = 0;
numc = 0;
memset(map, 0, sizeof(map));
getchar();
for (int i = 0; i < n; i ++)
{
for (int j = 0; j < m; j ++)
{
scanf("%c", &sb);
if (sb == '\\')
{
map[i * 3][j * 3] = 1;
map[i * 3 + 1][j * 3 + 1] = 1;
map[i * 3 + 2][j * 3 + 2] = 1;
}
if (sb == '/')
{
map[i * 3][j * 3 + 2] = 1;
map[i * 3 + 1][j * 3 + 1] = 1;
map[i * 3 + 2][j * 3] = 1;
}
}
getchar();
}
for (int i = 0; i < 3 * n; i ++)
{
for (int j = 0; j < 3 * m; j ++)
{
if (map[i][j] == 0)
{
bfs(i, j);
bfs2(i, j);
}
}
}
printf("Maze #%d:\n", tt ++);
if (numc)
printf("%d Cycles; the longest has length %d.\n\n", numc, maxx);
else
printf("There are no cycles.\n\n");
}
return 0;
}
第二個方法是:跟物理中的光學有關。。其實可以把每個牆壁看成鏡子,路徑看成光線。光射入鏡子以後反射的路徑是唯一的。然後每次就按照這個路徑搜索。。如果會射出邊界。。那麼這條路徑不可取。如果回射回起點,表明有回路。。這個方法寫起來比較煩。要考慮牆壁是‘\','/'和路徑入射方向。。但是時間比上一個方法快了許多。
#include <stdio.h>
#include <string.h>
int bo;
int n, m;
int xxx, yyy;
int www;
int numc;
int d[4][2] = {{-1,0},{0,1},{1,0},{0,-1}};
char map[80][80];
int vis[2][80][80];
int maxx;
void dfs(int x, int y, int f, int w, int bu)
{
if (x < 1 || x > n || y < 1 || y > m)
return;
if (bo == 0)
bo = 1;
else
{
if (x == xxx && y == yyy && w == www)
{
numc ++;
if (maxx < bu)
maxx = bu;
return;
}
}
vis[w][x][y] = 1;
int xx = x + d[f][0];
int yy = y + d[f][1];
if (f == 0)
{
if (map[xx][yy] == '\\')
{
dfs(xx, yy, 3, 1, bu + 1);
}
if (map[xx][yy] == '/')
{
dfs(xx, yy, 1, 1, bu + 1);
}
}
if (f == 1)
{
if (map[xx][yy] == '\\')
{
dfs(xx, yy, 2, 1, bu + 1);
}
if (map[xx][yy] == '/')
{
dfs(xx, yy, 0, 0, bu + 1);
}
}
if (f == 2)
{
if (map[xx][yy] == '\\')
{
dfs(xx, yy, 1, 0, bu + 1);
}
if (map[xx][yy] == '/')
{
dfs(xx, yy, 3, 0, bu + 1);
}
}
if (f == 3)
{
if (map[xx][yy] == '\\')
{
dfs(xx, yy, 0, 0, bu + 1);
}
if (map[xx][yy] == '/')
{
dfs(xx, yy, 2, 1, bu + 1);
}
}
}
int main()
{
int tt = 1;
while (scanf("%d%d", &m, &n) != EOF && n + m)
{
maxx = 0;
numc = 0;
getchar();
memset(map, 0, sizeof(map));
memset(vis, 0, sizeof(vis));
for (int i = 1; i <= n; i ++)
{
gets(map[i] + 1);
}
for (int i = 1; i <= n; i ++)
for (int j = 1; j <= m; j ++)
{
xxx = i; yyy = j;
if (vis[0][i][j] == 0)
{
www = 0;
bo = 0;
dfs(i, j, 0, 0, 0);
if (map[i][j] == '/')
{
bo = 0;
dfs(i, j, 3, 0, 0);
}
if (map[i][j] == '\\')
{
bo = 0;
dfs(i, j, 1, 0, 0);
}
}
if (vis[1][i][j] == 0)
{
www = 1;
if (map[i][j] == '/')
{
bo = 0;
dfs(i, j, 1, 1, 0);
}
if (map[i][j] == '\\')
{
bo = 0;
dfs(i, j, 3, 1, 0);
}
bo = 0;
dfs(i, j, 2, 1, 0);
}
}
printf("Maze #%d:\n", tt ++);
if (numc)
printf("%d Cycles; the longest has length %d.\n\n", numc / 2, maxx);
else
printf("There are no cycles.\n\n");
}
return 0;
}