深入理解 cocos2d-x 坐標系

首先對於初學的，帶大家認識 cocos2d-x 中坐標系的幾個概念，參考 http://blog.csdn.net/tskyfree/article/details/8292544。其他的往下看。

弄懂坐標系是開始開發的重要的一步，為了不讓大家頭暈，現在深入的為大家講解一下，本人原文地址：http://www.cnblogs.com/lyout/p/3292702.html。

首先我們添加兩個測試精靈(寬：27，高：40)到場景裡面：

		CCSprite *sprite1 = CCSprite::create("player.png");
		sprite1->setPosition(ccp(20, 40));
		sprite1->setAnchorPoint(ccp(0, 0));
		this->addChild(sprite1);

		CCSprite *sprite2 = CCSprite::create("player.png");
		sprite2->setPosition(ccp(-15, -30));
		sprite2->setAnchorPoint(ccp(1, 1));
		this->addChild(sprite2);

然後調試，在場景中大概是下圖這樣顯示（以左下角為坐標原點，從左到右為x方向，從下到上為y方向，廢話了：））：

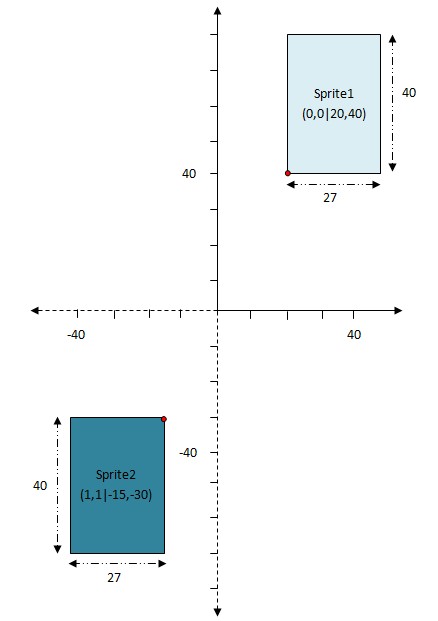
在cocos2d-x中，，我們暫且可以看作是精靈的中心位置，一般來說有每個方向有三種可能的值:0,0.5,1。上圖中紅色圓點即為各自的錨點，sprite1 錨點為 (0,0) 左下角，sprite2錨點為(1,1)在右上角。

現在我們來看看坐標系轉換，同樣地，我們先寫點測試代碼：

		CCPoint p1 = sprite2->convertToNodeSpace(sprite1->getPosition());
		CCPoint p2 = sprite2->convertToWorldSpace(sprite1->getPosition());
		CCPoint p3 = sprite2->convertToNodeSpaceAR(sprite1->getPosition());
		CCPoint p4 = sprite2->convertToWorldSpaceAR(sprite1->getPosition());

接著，再打印出各點的x,y值：

		CCLog("p1:%f,%f", p1.x, p1.y);
		CCLog("p2:%f,%f", p2.x, p2.y);
		CCLog("p3:%f,%f", p3.x, p3.y);
		CCLog("p4:%f,%f", p4.x, p4.y);

現在開始分析這四個常用坐標系轉換函數轉換後的值（有興趣的同學可以先算一算）。

由於cocos2d-x的坐標系（本地坐標系）是以左下角為坐標原點的，所以 ，那麼很明顯的：

p1就是相對於來說在sprite2坐標系中的位置，經過對比上圖，我們可以得到（20-(-42)，40-(-70)）即（62,110）

p2就是相對於來說在上圖坐標系中的位置，這樣我們可以計算出sprite1在sprite2坐標系中的位置：（20+(-42),40+(-70)），即（-22,-30）

p3就是相對於來說在sprite2坐標系中的位置，也就是（20-(-15)，40-(-30)）,即（35,70）

p4就是相對於來說在上圖坐標系中的位置，也就是（20+(-15),40+(-30)），即（5,10）

現在我們可以知道，計算方法。

好了，方法出來了，有興趣的可以做計算一下以下幾個坐標的值（先不要上機調試），然後回復我，差不多10個回復後我會貼出正確答案：

		CCPoint p1 = sprite1->convertToNodeSpace(sprite2->getPosition());
		CCPoint p2 = sprite1->convertToWorldSpace(sprite2->getPosition());
		CCPoint p3 = sprite1->convertToNodeSpaceAR(sprite2->getPosition());
		CCPoint p4 = sprite1->convertToWorldSpaceAR(sprite2->getPosition());