二分查找法在算法家族大類中屬於“分治法”,二分查找的過程比較簡單,代碼見我的另一篇日志,戳這裡!因二分查找所涉及的有序表是一個向量,若有插入和刪除結點的操作,則維護表的有序性所花的代價是O(n)。
就查找性能而言,二叉查找樹和二分查找不分伯仲,但是,就維護表的有序性而言,二叉排序樹無須移動結點,只需修改指針即可完成插入和刪除操作,且其平均的執行時間均為O(lgn),因此更有效。二叉查找樹,顧名思義,是一種可以用來二分查找的樹數據結構,其左孩子比父節點小,右孩子比父節點大,還有一個特性就是”中序遍歷“可以讓結點有序。在對關鍵字進行查找的時候,根據關鍵字與根節點的關鍵字比較的結果,分別選擇繼續與其左子樹或者右子樹進行比較,直到找到所查找的關鍵字或者訪問節點的左右子樹不存在(沒找到關鍵字)則退出!
二叉查找樹的主要操作有:插入關鍵字,查找關鍵字,刪除關鍵字。下面分別對這三個步驟做詳細描述和算法實現。
為了方便,我將二叉查找樹實現為一個類,結構如下:
typedef Node_ * Node_ * Node_ *~**
1. 插入關鍵字的過程如下所示:
其中的compEQ和compLT為2個宏定義,用來比較兩個關鍵字的大小。
2. 查找關鍵字的過程比較簡單,和二分查找方法類似,代碼如下:
Node**current =(current !=(compEQ(data, current->= compLT(data, current->data) ?->left : current->
3. 刪除關鍵字的過程分為2種情況討論:單孩子的情況和左右孩子的情況。
1> 單孩子情況分析:
如果刪除的節點有左孩子那就把左孩子頂上去,如果有右孩子就把右孩子頂上去,so easy!如圖所示:
好了,二叉查找樹的代碼告一段落,我們在來分析一下二叉查找樹的插入過程,假如有以下序列:<4, 17, 16, 20, 37, 38, 43>,則會生成如下所示二叉樹:
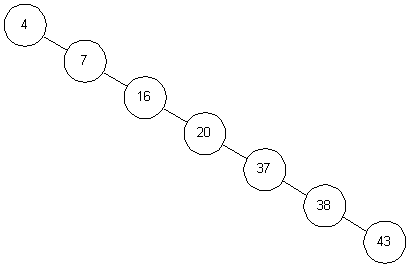
這已經完全退化成了一個單鏈表,勢必影響到關鍵字的查找過程。不過總會有解決辦法的,下一篇博客我將繼續這個話題,對普通二叉樹經過旋轉,即使用平衡二叉樹,使其保持最壞復雜度在O(logN)。
謝謝大家的閱讀,希望能夠幫到大家!PS:文章中部分圖片利用了博客園另外一篇文章的插圖(戳這裡)!
Published by Windows Live Write!