題目:給出兩個鏈表的頭指針,比如head1和head2,判斷這兩個鏈表是否相交。這裡為了化簡,我們假設兩個鏈表均不帶環。
方案一:蠻力法。一般我們都能想到的,就是從head1開始,逐個與head2中的每個結點的地址比較,看是否相等,如果不等,則head1移動到下一個結點,繼續和head2中的每一個結點的地址比較;如果找到相等,則這兩個鏈表相交;直到head1==NULL,則不相交。注意為了避免存在相同的元素,我們采取比較地址的方法,而不是比較元素,在判斷鏈表裡是否有環的時候,也是采用比較地址的方法。時間復雜度為O(N*N)。
方案二:利用空間換時間的做法。采用計數法。如果兩個鏈表相交則說明該鏈表有相同的結點。而地址有時其唯一的標示,所以我們還是可以采取和方案一一樣的比較地址的方案。只不過我們使用哈希表,將鏈表head1每個結點的地址進行hash取值,然後遍歷haed2鏈表一遍,我們就可以得出是否有相同的結點,也就是是否存在相交。這裡是時間復雜度為:O(N)=O(Lenght(head1)+Length(head2))+輔助空間O(Lenght(head1))。
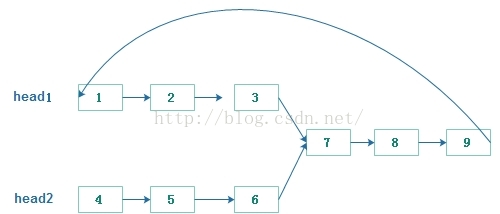
方案三:由於鏈表裡沒有環。那麼我們可以將該問題進行轉化,將head1頭結點接到head2的尾部,這樣我們就可以通過判斷head2鏈表裡有沒有環來進行判斷,他們是否相交。具體如下圖所示。
如果head2沒有環,則證明這兩個鏈表不相交,如果head2裡有環,則證明這兩個鏈表相交。
具體如何判斷鏈表是否有環。
方案四:由於只需要判斷這兩個鏈表時否相交,如果相交,那麼這兩個鏈表的最後一個結點一定是同一個,它們是‘Y’字形的;但是如果不相交那就不存在這個特點。所以我們可以通過兩次遍歷,得到兩個鏈表的最後一個結點,然後通過比較這兩個鏈表的地址是否相同來判斷它們是否相交。時間復雜度:O(Lenght(head1)+Length(head2))=O(N)。
這個題雖然比較簡單,只是方案三裡有一點兒值得學習的地方,就是我們可以將不熟悉的問題轉化為我們熟悉的問題,這樣在解決問題的時候就會簡單很多。有些問題正面解決很難,但是通過轉化以後就會很簡單。