程序師世界是廣大編程愛好者互助、分享、學習的平台，程序師世界有你更精彩！
設為首頁 加入收藏
首頁
編程語言
C語言|JAVA編程
Python編程
網頁編程
ASP編程|PHP編程
JSP編程
數據庫知識
MYSQL數據庫|SqlServer數據庫
Oracle數據庫|DB2數據庫
 程式師世界 >> 編程語言 >> C語言 >> C++ >> 關於C++ >> 數字之魅：子數組之和的最大值[二維]+[三維]

數字之魅：子數組之和的最大值[二維]+[三維]

編輯：關於C++

題目：如何求出一個二維數組中的最大子數組之和。

方案一：暴力破解-枚舉法。對於一個二維數組我們列舉出每一個子數組值的大小，然後進行比較，這樣就可以得到最大的和了。其時間復雜度為：O(N*N*M*M*Sum的時間復雜度)[N表示行數，M表示列數,Sum是求解子矩陣的和]。由於Sum函數求和也是采用循環，足見這個時間復雜度可是相當的大。

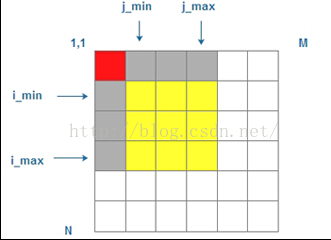
方案二：先計算出以左上角的元素(1,1)和當前元素(i,j)為頂點對的子矩陣的部分和，部分和的計算如下圖(一)所示，我們可以看出：以(i_min,j_min),(i_min,j_max),(i_max,j_min),(i_max,j_max)為頂點的矩形區域的元素和為：Sum[i_max][j_max] = Sum[i_max][j_max]-Sum[i_min-1][j_max]-Sum[i_max][j_min-1]+Sum[i_min-1][j_min-1]。也就是在已知部分和的基礎上就可以在0(1)的時間內得到任意矩形的元素之和。

那麼如何得到部分和呢?

如圖二所示，在更小的“部分和”基礎上，也能以O(1)得到新的“部分和”。公式為：Sum[i][j]=Sum[i-1][j]+Sum[i][j-1]-Sum[i-1][j-1]+arr[i][j]這裡的arr[i][j]是矩陣中的arr[i][j]的值。因此在這裡我們可以用O(N*M)來得到部分和。這裡我們主要去掉了計算法子矩陣和的時間復雜度，所以其時間復雜度為：O(N*N*M*M).相比與方案一有所提高。

 

\
圖一

 

 

\

 

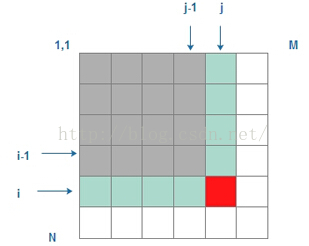
 圖二

方案三：其實我們仔細的想一想，就可以發現，它的最簡單的原型是求一維數組中的最大值。那麼基於這個啟發，我們可以把問題從二維轉化為一維以提高算法性能。假設已經確定了矩陣區域的上下邊界，知道矩陣區域的上下邊界分布是第a行和第c行，就把每列的第a行和第c行之間的元素看成一個整體。即求數組：(merge[1],merge[2],merge[3]....).merge[i]=arr[a][i]+arr[b][i]+..+arr[c][i].

這樣我們可以枚舉矩形的上下邊界，然後再用一維情況下的方法確定左右邊界，相當於一維數組中的一個元素(通過子矩陣部分和可以在O(1)時間內計算出整體之和)，就可以得到二維問題的解。新方法的時間復雜度為：O(N*N*M)=O(N*N*N)。具體過程如下圖三所示：

 

\

 

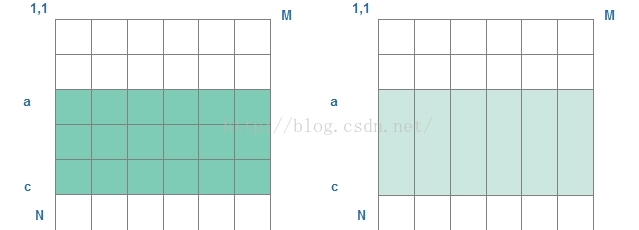
圖三

方案一的具體實現代碼：
 

int arr[N][M];
int Max(int x,int y)//得到最大值;
{
	return  (x>y)?x:y;
}
int Sum(int imin,int imax,int jmin,int jmax)//得到子矩陣的和，時間復雜度為O(N*N)；
{
	int sum=0;
	for(int i=imin;i<=imax;i++)
		for(int j=jmin;j<jmax;j++)
			sum+=arr[i][j];
	return sum;
}
int MaxSum(int *arr,int m,int n) //得到子矩陣的最大值；
{
	int maximum=0;
	for(int i_min=1;i_min<=n;i_min++)
		for(int i_max=i_min;i_max<=n;i_max++)
			for(int j_min=1;j_min<=m;j_max++)
				for(int j_max=j_min;j_max<=m;j_max++)
					maximum=Max(maximum,Sum(i_min,i_max,j_min,j_max));
	return maximum;
}

 

方案二的具體實現代碼：
 

int arr[N][M];
int Sum[N][M];//存儲部分和的數組；
int Max(int x,int y)//得到最大值;
{
	return  (x>y) ? x:y;
}
void GetSum()//預處理得到部分和；
{
	for(int i=0;i<=n;i++)
		Sum[i][0]=0;//邊界值；
	for(int j=0;j<=n;j++)
		Sum[0][j]=0;//邊界值；真正的部分和數據是從Sum[1][1]開始的;
	for(i=1;i<=n;i++)
		for(j=1;j<=m;j++)
			Sum[i][j]=Sum[i-1][j]+Sum[i][j-1]-Sum[i-1][j-1]+arr[i][j]
}
inline int Sum(int i_min,int i_max,int j_min,int j_max)//調用比較頻繁，可設置為內聯函數，提高效率。和方案一相比，其時間復雜度為O(1).
{
	return Sum[i_max][j_max]-Sum[i_min-1][j_max]-Sum[i_max][j_min-1]+Sum[i_min-1][j_min-1];
}
int MaxSum(int *arr,int m,int n)
{
	int maximum=0;
	for(int i_min=1;i_min<=n;i_min++)
		for(int i_max=i_min;i_max<=n;i_max++)
			for(int j_min=1;j_min<=m;j_max++)
				for(int j_max=j_min;j_max<=m;j_max++)
					maximum=Max(maximum,Sum(i_min,i_max,j_min,j_max));
	return maximum;
}

方案三的具體實現代碼：

#include <iostream>  
#include <algorithm>  
using namespace std;  
#define LEN 888 
int arr[LEN][LEN];  
long long Sum[LEN][LEN];  


inline long long MatrixSum(int s, int t, int i, int j)  
{  
	return Sum[i][j]-Sum[i][t-1]-Sum[s-1][j]+Sum[s-1][t-1];  
}  


int main()  
{  
	int row, col, i, j;  
	cout<<"please input the row and col of the array:"<<endl;
	cin >> row >> col;  
	cout<<"please input the data of the array:"<<endl;
	for (i=1; i<=row; i++)  //輸入數據；
		for (j=1; j<=col; j++)  
			cin >> arr[i][j];  


	for (i=0; i<=row; i++)  //設置邊界線；
		Sum[i][0] = 0;  
	for (j=0; j<=col; j++)  
		Sum[0][j] = 0;  


	for (i=1; i<=row; i++)  // 預處理計算矩陣的部分和 
		for (j=1; j<=col; j++)  
			Sum[i][j] = arr[i][j]+Sum[i-1][j]+Sum[i][j-1]-Sum[i-1][j-1];  


	int a, c;  
	long long MaxSum = arr[1][1]; //初始值的設置； 
	for (a=1; a<=row; a++)  
		for (c=a; c<=col; c++)  // 將子矩陣上下邊界設為第a行和第c行，求取取最大值  
		{  
			long long Tail = MatrixSum(a, 1, c, 1);  //合並列；
			for (j=2; j<=col; j++)  //按一維數組向後枚舉；
			{  
				Tail = max( MatrixSum(a, j, c, j), MatrixSum(a, j, c, j)+Tail);   
				MaxSum = max(Tail, MaxSum);  
			}  
		}  


		cout <<"最大的子矩陣和為："<< MaxSum<<endl;  
		system("pause");
		return 0;
}

運行結果如下：

 

\

 

擴展問題1：如果二維數組也是首尾相連，像一條首尾相連的帶子，算法會如何改變?其實現代碼如下：

#include

#include

using namespace std;

#define LEN 1003

int arr[LEN][LEN];

long long Sum[LEN][LEN];

inline long long MatrixSum(int s, int t, int i, int j)

{

return Sum[i][j]-Sum[i][t-1]-Sum[s-1][j]+Sum[s-1][t-1];

}

int main()

{

int row, col, i, j;

cout<<"please input the row and col of the array:"<> row >> col;

cout<<"please input the data of the array:"<> arr[i][j];

for (i=0; i<=row; i++)

Sum[i][0] = 0;

for (j=0; j<=col; j++)

Sum[0][j] = 0;

// 計算矩陣的部分和

for (i=1; i<=row; i++) //計算部分和;

for (j=1; j<=col; j++)

Sum[i][j] = arr[i][j]+Sum[i-1][j]+Sum[i][j-1]-Sum[i-1][j-1];

int a, c;

long long MaxSum = arr[1][1]; // 上下邊界不會跨過第n行和第1行

for (a=1; a<=row; a++)

for (c=a; c<=row; c++)

{

// 將子矩陣上下邊界設為第a行和第c行

// 左右邊界不會跨過第m列和第1列

long long Tail = MatrixSum(a, 1, c, 1);

for (j=2; j<=col; j++)

{

Tail = max(MatrixSum(a, j, c, j),

MatrixSum(a, j, c, j)+Tail);

MaxSum = max(Tail, MaxSum);

}

long long Sum = MatrixSum(a, 1, c, 1); // 左右邊界會跨過第n列和第1列

long long Start = Sum;

int sind = 1;

for (i=2; i<=col; i++)

{

Sum += MatrixSum(a, i, c, i);

if (Sum > Start) {Start = Sum; sind = i;}

}

Tail = MatrixSum(a, col, c, col);

int tind = col;

for (j=col-1; j>=1; j--)

{

Sum += MatrixSum(a, j, c, j);

if (Sum > Tail) {Tail = Sum; tind = j;}

}

if (sindMaxSum)

MaxSum = Start+Tail;

}

cout <<"最大的子矩陣和為："<< MaxSum<


擴展問題2：求3維矩陣，也就是長方體中子長方體的最大值?

長方體我們需要求子長方體的最大值，那麼可以想象一下!其實思路和二維是一樣的，主要是采取降維的思路，這樣可以把復雜的問題簡單化。主要關鍵還是在求部分和，其求解公式如下：

PS[i][j][k] = A[i][j][k]+PS[i-1][j][k]+PS[i][j-1][k]+PS[i][j][k-1]-PS[i-1][j-1][k]-PS[i-1][j][k-1]-PS[i][j-1][k-1]+PS[i-1][j-1][k-1]; [i,j,k形象點兒可分別代表其長寬高]

其時間復雜度為：O(N*N*M*M*Q)=O(N^5)。可以得出：一維是O(N)，二維是O(N*N)，三維是O(N^5).具體實現代碼如下：

#include

#include

using namespace std;

#define LEN 500

int arr[LEN][LEN][LEN];

int Sum[LEN][LEN][LEN];

inline int MaxCubeSum(int a, int b, int c, int d, int i, int j)

{

return Sum[b][d][j]-Sum[a-1][d][j]-Sum[b][c-1][j]-Sum[b][d][i-1]+

Sum[a-1][c-1][j]+Sum[a-1][d][i-1]+Sum[b][c-1][i-1]-Sum[a-1][c-1][i-1];

}

int main()

{

int row, col, high, i, j, k;

cout<<"please input the row, col and high of the array:"<> row >> col >>high;

cout<<"please input the data of the array:"<> arr[i][j][k];

for (i=0; i<=row; i++)

for (j=0; j<=col; j++)

Sum[i][j][0] = 0;

for (i=0; i<=row; i++)

for (k=0; k<=high; k++)

Sum[i][0][k] = 0;

for (j=0; j<=col ; j++)

for (k=0; k<=high; k++)

Sum[0][j][k] = 0;

// 計算長方體的部分和

for (i=1; i<=row; i++)

for (j=1; j<=col; j++)

for (k=1; k<=high; k++)

Sum[i][j][k] = arr[i][j][k]+Sum[i-1][j][k]+Sum[i][j-1][k]+Sum[i][j][k-1]-Sum[i-1][j-1][k]-Sum[i-1][j][k-1]-Sum[i][j-1][k-1]+Sum[i-1][j-1][k-1];

int a, b, c, d;

int MaxSum = arr[1][1][1];

// 限制第一維的取值范圍

for (a=1; a<=row; a++)

for (b=a; b<=row; b++)

// 限制第二維的取值范圍

for (c=1; c<=col; c++)

for (d=c; d<=col; d++)

{

// 只剩下最後一維沒有確定，利用一維部分和的方法

int Tail = MaxCubeSum(a,b,c,d,1,1);

for (j=2; j<=k; j++)

{

int cur = MaxCubeSum(a,b,c,d,j,j);

Tail = max(Tail+cur, cur);

MaxSum = max(Tail, MaxSum);

}

}

cout <<"最大的子矩陣和為："<< MaxSum<

 

  1. 上一頁:
  2. 下一頁:
關於C++
數據結構基礎(13)

采用鏈式存儲的棧成為鏈式棧(或簡稱鏈棧), 鏈棧的優點是便於
C++、Java、JavaScript中的日志(log)

編程思想之日志記錄什麼是log？相信你一定用日記寫過點滴心事
算法練習系列—hiho1048 狀態壓縮一(鋪地磚)

  編程之美的課後題也有一個和整個題目一樣的。（P
dubbo+spring+zookeeper之demo制作

兩個工程，最好使用maven比較好，但是由於時間有限，所以暫
利用堆排序實現學生成績管理

1　引言排序是計算機數據處理及其它許多軟件系統
Pentium III處理器的單指令多數據流擴展指令（2）

關鍵字 :Pentium,處理器,單指令多數據
相關文章
閱讀排行榜
STM32M CUBE實現printf打印調試信息以及實現單字節接收 POJ 2299 Ultra HDU3294 Girls&#39; research HDU 1253 勝利大逃亡 [LeetCode][Java] Spiral Matrix II POJ 3169 Layout（差分約束系統） LeetCode Pascal&#39;s Triangle II HDU 3911 Black And White（線段樹區間合並） hdu 1394(BIT求逆序數) C++入門學習——explicit關鍵字的作用 C/C++誤區四：char c = getchar();
熱門圖文
ecshop後台登錄超時session過期的解決辦法 PHP用身份證號獲取星座和生肖的方法 ArrayList集合，arraylist集合排序 一個簡單的記事本代碼03 php模擬post上傳圖片實現代碼 亂碼的解決，亂碼解決 在ASP.NET 2.0中操作數據之五十八：在程序啟動階段緩存數據 ubantu-有沒有好文推薦？關於Ubantu下安裝openstack的？
欄目導航
C++基礎知識C++入門知識關於C++
Copyright © 程式師世界 All Rights Reserved