很多計算機科學家認為排序是算法研究中最基礎的問題，不僅如此，有的學者指出對待解決問題先進行排序，可能有利於的問題的分析以及求解思路的產生。
排序算法 1 插入排序 2 歸並排序 3 堆排序 31 堆 311 維護堆的性質 312 建堆 32 堆排序算法 33 優先隊列 4 快速排序 5 計數排序 6 基數排序和桶排序 7 總結和要求
插入排序是穩定排序，時間復雜度是O(n^2)。思路是采用從後向前依次挪位置，直到key的位置找到，然後放進去。
void insert_sort(vector& A){
for (int i = 1; i < A.size(); i++){
int key = A[i];
int j = i - 1;
while (j>=0 && A[j] > key){
A[j + 1] = A[j];
j--;
}
A[j+1] = key;
}
}
int main()
{
srand(time(0));
vector nums(10);
for (int i = 0; i < nums.size(); i++){
nums[i] = rand() % 20;
}
for (auto val : nums)
cout << val << " ";
cout << endl;
insert_sort(nums);
cout << "insert-sort: " << endl;
for (auto val : nums)
cout << val << " ";
cout << endl;
return 0;
}
插入排序運行結果如圖
![插入排序代碼示例](https://www.aspphp.online/bianchen/UploadFiles_4619/201701/2017010315022951.png "\")
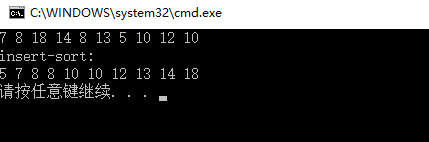
歸並排序，復雜度O(nlgn)。
思路是每次將數組分成兩部分，然後對各部分進行排序，通過合並（歸並）操作將兩段已經排序過的數組進行整合，形成新的排序數組的順序。
void merge(vector& nums, int left, int mid, int right){
vector L(nums.begin() + left, nums.begin() + mid+1);
vector R(nums.begin() + mid + 1, nums.begin() + right+1);
L.push_back(INT_MAX);
R.push_back(INT_MAX);
int i = 0;
int j = 0;
for (int k = left; k <= right; k++){
if (L[i] <= R[j])
nums[k] = L[i++];
else
nums[k] = R[j++];
}
}
void merge_sort(vector& nums, int left, int right){
if (left < right){
int mid = (left + right) / 2;
merge_sort(nums, left, mid);
merge_sort(nums, mid + 1, right);
merge(nums, left, mid, right);
}
}
int main()
{
srand(time(0));
vector nums(10);
for (int i = 0; i < nums.size(); i++){
nums[i] = rand() % 20;
}
for (auto val : nums)
cout << val << " ";
cout << endl;
merge_sort(nums, 0, nums.size() - 1);
cout << "merge-sort: " << endl;
for (auto val : nums)
cout << val << " ";
cout << endl;
return 0;
}
運行結果如圖：
![歸並排序圖示](https://www.aspphp.online/bianchen/UploadFiles_4619/201701/2017010315022942.png "\")
堆的性質的維護，以下都以最大堆為例。
堆的維護的主要思想是“逐層下降”。舉例：某個結點i, 假設其左右子結點left(i)，right(i)都已經是最大堆，那麼需要調節(或者說是調換)i, left(i), right(i)的值，並保證調換後的子樹繼續調換下去直到子樹繼續滿足堆的性質。首先，如果結點i的值大於左右子結點的值(即i的值是三個值中的最大值)，則不需要調換，因為左右子結點均滿足堆的性質，同時結點i也滿足了結點值大於等於子結點的值，所以整棵樹就是最大堆（也有叫大頂堆）。其次，如果結點i的值不是三個中的最大值，不妨設左結點的值最大（即左結點的值比右結點以及i的值都大），則把i的值跟左結點的值調換，此時i, left, right滿足了父結點值大於等於左右子結點值的情況，那麼被調換後的左結點的值（變小了），以該結點為參考對象，它因為變小了，那麼它還滿足堆的要去嗎，所以需要繼續進行檢測和調換，即逐層的進行下去，直到原來的i值滑落到穩定的位置。時間復雜度是O(lgn)。以下是算法代碼的具體驗證：
/*
最大堆的維持輸入參數是一個數組，和一個小標i，
表示維持i到heap-size使該范圍的二叉樹為一個最大堆。
注意一個前提：結點i的左右子樹都已經是最大堆。
此處假設a的數組長度size與heap-size一致。
*/
void max_heapify(vector& a, int i){
int largest = i;
int left = 2 * i+ 1;//因為數組的下標是從0開始的，與算法表述裡的數組下標都是從1開始的，故應該進行相應轉化，以使其對應
int right = 2 * i + 2;
if (left < a.size() && a[left] > a[i])
largest = left;
if (right < a.size() && a[right] > a[largest])
largest = right;
if (largest != i){
int tmp = a[i];
a[i] = a[largest];
a[largest] = tmp;
max_heapify(a, largest);
}
}
int main()
{
vector a(10, 0);
for (int i= 0; i < 10; i++)
a[i] = 10-i;
for (auto val : a)
cout << val << " ";
cout << endl;
a[0] = 1;
max_heapify(a, 0);
for (auto val : a)
cout << val << " ";
return 0;
}
![維持最大堆化示例](https://www.aspphp.online/bianchen/UploadFiles_4619/201701/2017010315022923.png "\")
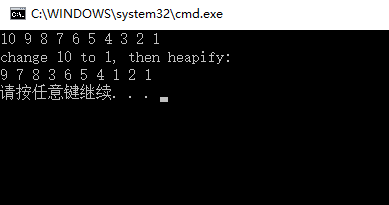
知道堆的性質的維護方法以後，建堆的思路也就有了，就是從已經堆化的部分逐步往上調用最大堆化函數，使整個數組逐漸全部滿足堆的要求。底層的每一個單獨的葉結點是滿足堆的要求的，葉結點有A.length - A.length/2 個。所以從葉結點的父結點那一層開始建堆，這些點的下標范圍是:1– A.length/2 建堆的過程是從後往前每個點調用最大堆化函數，所以可能會有人認為復雜度是O(nlgn)，這個結果雖然正確但不是漸近緊確的，經過證明可以得到建堆過程的一個更緊確的界：O(n)。證明方法請參考算法導論。一下是建堆過程的代碼示例：
void build_max_heap(vector& a){
for (int i = a.size() / 2-1; i >= 0; i--)
max_heapify(a, i);
}
int main()
{
srand(time(0));
vector a(10, 0);
for (int i= 0; i < 10; i++)
a[i] = rand()%20;
for (auto val : a)
cout << val << " ";
cout << endl;
cout << "buid max-heap: " << endl;
build_max_heap(a);
for (auto val : a)
cout << val << " ";
cout << endl;
return 0;
}
![建堆代碼示例](https://www.aspphp.online/bianchen/UploadFiles_4619/201701/2017010315022977.png "\")
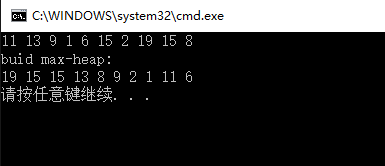
給定數組A，如要對數組A進行排序輸出，則第一步是根據A數組建堆，此步時間復雜度為O(n), 建好堆的數組A的最大元素一定在A[1]（算法描述裡數組的首個位置下標為1，代碼裡數組的首個位置下標為0，此處再做一次區分）。那麼我把A[1]與A[n]調換，則此時數組裡的最大元素已經跑到數組的最後位置，那麼數組的前n-1個元素是什麼樣的情況，由於A[1]和A[n]互換，所以新的A[1]結點以及其左右子結點組成的triangle不一定滿足最大堆的性質了（父結點的值大於等於子結點的值），但是其左右子結點對應的樹，依然是滿足堆的性質的，所以對於A的前n-1個元素，只需要對A[1]結點調用維持堆化過程，整個n-1個元素就又變成了新的最大堆，其第一個元素A[1]就是n-1個元素中的最大值，也即是數組A中的次大值, 此時把A[1]與A[n-1]交換，則次大值放入了正確的位置，依次類推，直到位置2-n都放入了相應的值，則排序結束，時間復雜度O(nlgn)。以下是代碼示例：
void max_heapify(vector& a, int i, int heap_size){
int largest = i;
int left = 2 * i + 1;//因為數組的下標是從0開始的，與算法表述裡的下標略微不對應，故應該用此表述
int right = 2 * i + 2;
if (left < heap_size && a[left] > a[i])
largest = left;
if (right < heap_size && a[right] > a[largest])
largest = right;
if (largest != i){
int tmp = a[i];
a[i] = a[largest];
a[largest] = tmp;
max_heapify(a, largest, heap_size);
}
}
void build_max_heap(vector& a, int heap_size){
for (int i = heap_size / 2-1; i >= 0; i--)
max_heapify(a, i, heap_size);
}
void heapsort(vector& a){
int n = a.size();
build_max_heap(a, a.size());
for (int i = n - 1; i >= 1; i--){
int tmp = a[0];
a[0] = a[i];
a[i] = tmp;
max_heapify(a, 0, i);
}
}
int main()
{
srand(time(0));
vector a(10, 0);
for (int i= 0; i < 10; i++)
a[i] = rand()%20;
for (auto val : a)
cout << val << " ";
cout << endl;
cout << "heap sort: " << endl;
heapsort(a);
for (auto val : a)
cout << val << " ";
cout << endl;
return 0;
}
![堆排序代碼示例](https://www.aspphp.online/bianchen/UploadFiles_4619/201701/2017010315022938.png "\")
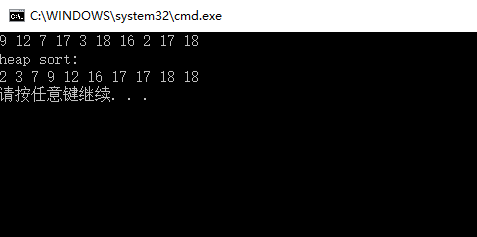
略
快排是排序中的經典算法，最壞情況下復雜度是O(n^2)，期望的時間復雜度是O(nlgn)。主要思想是：每次給一個元素x=A[r]找到其特定的位置，使左邊的元素都小於x，右側的值都大於x。如何實現就是用i來標記小於x的個數，然後沒遇到一個小於x的值，就把i的范圍值加1，並把這個較小的值置換進小於x的區域裡。最後r前的元素都遍歷完了，就把元素x與i+1位置上的元素置換，因為i+1這個位置，對應的就應該是x，也就是說值x就對應了排好序的數組情況下的i+1的位置。剩下的對i+1位置之前之後的兩段分別排序就行，遞歸進行。
int partition(vector& a, int p, int r){
int x = a[r];
int i = p - 1;
for (int j = p; j < r; j++){
if (a[j] < x){
i++;
swap(a[i], a[j]);
}
}
swap(a[i + 1], a[r]);
return i + 1;
}
void quicksort(vector& a, int p, int r){
if (p < r){
int q = partition(a, p, r);
quicksort(a, p, q - 1);
quicksort(a, q + 1, r);
}
}
int main()
{
srand(time(0));
vector a(10);
for (int i = 0; i < 10; i++){
a[i] = rand() % 100;
}
for (auto val : a)
cout << val << " ";
cout << endl;
cout << "quicksort: " << endl;
quicksort(a, 0, a.size() - 1);
for (auto val : a)
cout << val << " ";
cout << endl;
return 0;
}
以下是隨機版本的快排代碼示例
int partition(vector& a, int p, int r){
int x = a[r];
int i = p - 1;
for (int j = p; j < r; j++){
if (a[j] < x){
i++;
swap(a[i], a[j]);
}
}
swap(a[i + 1], a[r]);
return i + 1;
}
int randomized_partition(vector& a, int p, int r){
int i = rand() % (r-p+1)+p;//i是從[p, r]之間的一個隨機數
swap(a[i], a[r]);
return partition(a, p, r);
}
void quicksort(vector& a, int p, int r){
if (p < r){
int q = randomized_partition(a, p, r);
quicksort(a, p, q - 1);
quicksort(a, q + 1, r);
}
}
int main()
{
srand(time(0));
vector a(10);
for (int i = 0; i < 10; i++){
a[i] = rand() % 100;
}
for (auto val : a)
cout << val << " ";
cout << endl;
cout << "quicksort: " << endl;
quicksort(a, 0, a.size() - 1);
for (auto val : a)
cout << val << " ";
cout << endl;
return 0;
}
![隨機版本快排代碼示例](https://www.aspphp.online/bianchen/UploadFiles_4619/201701/2017010315022967.png "\")
在已知待排序的元素范圍為0-k之間時，可使用計數排序。當k=O(n)時，此時運行時間為Θ(n)。思路是：記錄對應元素出現的次數，則可以推算出改元素在排序後中的數組的下標。
void counting_sort(vector& A, vector& B, int k){
vector C(k + 1, 0);
for (int i = 0; i < A.size(); i++)
C[A[i]]++;
for (int i = 1; i < C.size(); i++)
C[i] += C[i - 1];
for (int i = A.size() - 1; i >= 0; i--){
B[C[A[i]]-1] = A[i];
C[A[i]]--;
}
}
int main()
{
srand(time(0));
vector nums(10);
for (int i = 0; i < nums.size(); i++){
nums[i] = rand() % 20;
}
for (auto val : nums)
cout << val << " ";
cout << endl;
vector B(10);
counting_sort(nums, B, 20);
cout << "counting-sort: " << endl;
for (auto val : B)
cout << val << " ";
cout << endl;
return 0;
}
![計數排序示例](https://www.aspphp.online/bianchen/UploadFiles_4619/201701/2017010315023024.png "\")
基數排序，要求n個數，每個數d位，每位有k個可能，則復雜度為O(d(n+k))。基數排序與快排的比較：哪一個排序算法更適合取決於具體實現和底層硬件的特性（例如，快速排序通常比基數排序能更有效的使用硬件的緩存），以及輸入數據的特性。另外，當主存容量比較寶貴時，我們可能更會傾向於像快速排序這樣的原址排序算法。
桶排序假設輸入數據服從均勻分布，並位於[0, 1)之間。最壞時間復雜度O(n^2)，平均時間復雜度O(n)。只要輸入數據滿足下列性質：所有桶的大小的平方和與總元素成線性關系，那麼桶排序就能在線性時間完成。桶排序思路是建立若干桶，然後把數據分入桶中，然後各個桶內進行插入排序，最後總的輸出。
今天和伙伴進行了討論，發現算法的實現要求熟練，即動手就能把代碼實現，這算是基本的要求。然後是對時間復雜度的證明。
參考 算法導論
