【poj 2411】Mondriaan's Dream 狀態壓縮DP

Mondriaan’s Dream

Time Limit: 3000MS Memory Limit: 65536K
Total Submissions: 14345 Accepted: 8273

Description

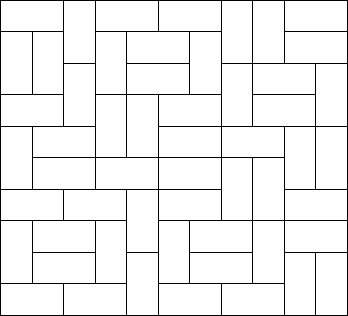
Squares and rectangles fascinated the famous Dutch painter Piet Mondriaan. One night, after producing the drawings in his ‘toilet series’ (where he had to use his toilet paper to draw on, for all of his paper was filled with squares and rectangles), he dreamt of filling a large rectangle with small rectangles of width 2 and height 1 in varying ways.

Expert as he was in this material, he saw at a glance that he’ll need a computer to calculate the number of ways to fill the large rectangle whose dimensions were integer values, as well. Help him, so that his dream won’t turn into a nightmare!
Input

The input contains several test cases. Each test case is made up of two integer numbers: the height h and the width w of the large rectangle. Input is terminated by h=w=0. Otherwise, 1<=h,w<=11.

Output

For each test case, output the number of different ways the given rectangle can be filled with small rectangles of size 2 times 1. Assume the given large rectangle is oriented, i.e. count symmetrical tilings multiple times.
Sample Input
1 2
1 3
1 4
2 2
2 3
2 4
2 11
4 11
0 0

Sample Output
1
0
1
2
3
5
144
51205

Source

Ulm Local 2000

題目鏈接：http://poj.org/problem?id=2411

題意：
經典的鋪磚塊問題；

思路：
1.《=11的數據范圍–》狀態壓縮DP
遞推式：

dp[i]+=tmp[j];

2.滾動數組dp[i]與前一行達到i狀態的方案數

代碼2：（）dfs版

#include
#include 
using namespace std;
long long  f[12][1<<12];//fullfil level i,the imfactto sta   ; target f[m][0];
int n,m;
int num=0;
int F1[1<<23];
int F2[1<<23];
void dfs(int i,int fromm,int too)
{
    if(i>n) return;
    if(i==n)   
    {   
    num++;  
    F1[num]=fromm;
    F2[num]=too;    
    }
    dfs(i+1,(fromm<<1)+1,too<<1);
    dfs(i+1,fromm<<1,(too<<1)+1);
    dfs(i+2,fromm<<2,too<<2);
}
int main()
{
    while(cin>>n>>m)
    {  
    if(n==0&&m==0)
    return 0;
    num=0;
    memset(f,0,sizeof(f));

    f[0][0]=1;
    dfs(0,0,0);
    for(int i=0;i<=m-1;i++)
      for(int j=1;j<=num;j++)
          {
            f[i+1][F2[j]]+=f[i][F1[j]];
          }


   cout<

代碼：dp

#include
#include
#include
#include
using namespace std;
#define M (1<<11)+10
long long tmp[M];
long long  dp[M];
int n,m;
bool mark[M];
long long  b[13];
bool C(int x)
{
    while(x)
    {
        if(x&1)
        {
            x>>=1;
            if(!(x&1)) return 0; //第j列是1則第j+1列必須是1 
            x>>=1;
        }
        else x>>=1;
    }
    return 1;
}
void init()
{
    memset(mark,0,sizeof(mark));
    memset(tmp,0,sizeof(tmp));
    for(int i=0;in) swap(n,m);
        init();
        solve();
    }


}