在之前的博文中我們已經將頂層的網絡結構都介紹完畢,包括卷積層、下采樣層、全連接層,在這篇博文中主要有兩個任務,一是整體貫通一下卷積神經網絡在對圖像進行卷積處理的整個流程,二是繼續我們的類分析,這次需要進行分析的是卷積層和下采樣層的公共基類:partial_connected_layer。
一、卷積神經網絡的工作流程
首先給出經典的5層模式的卷積神經網絡LeNet-5結構模型:
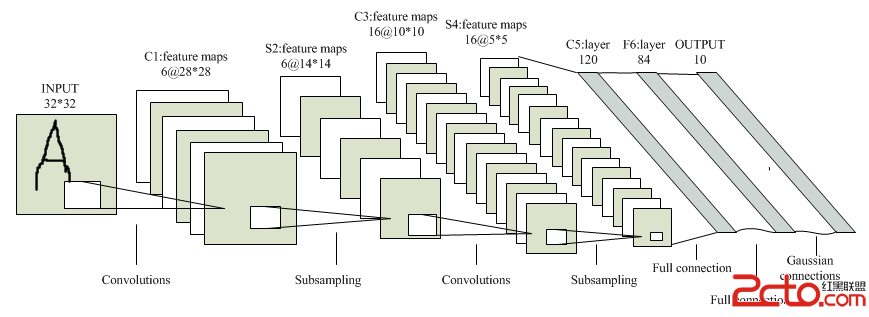
這是一個典型的卷積層-下采樣層-卷積層-下采樣層-卷積層-全連接層模式的CNN結構,接下裡觀察在我們的程序實例中對網絡的初始化情況:
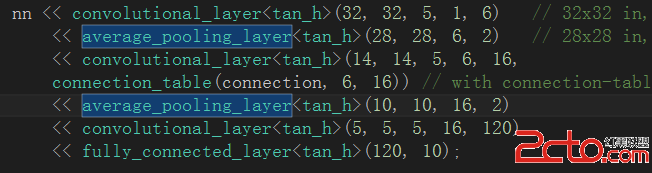
(1)卷積層C1:輸入圖像的尺寸為32*32,卷積核尺寸(卷積窗口尺寸)為5*5,輸入數據模板數量為1,卷積核模板種類為6個,導致C1層對每個輸入的圖像進行卷積操作之後,得到6個卷積特征模板輸出,並且卷積後圖像的尺寸變為32-5+1=28
(2)均值下采樣層S2:輸入圖像的尺寸為28*28,輸入數據矩陣的個數為6個,均值下采樣是的鄰域窗口為2*2,。這裡需要強調的一點是S2和C1是相鄰層,S2以C1層的輸出為輸入,因此S2的輸入尺寸等於C1的輸出尺寸,S2的輸入特征模板個數等於C1的輸出特征模板個數,並且這兩層之間的連接方式為全連接。S2層由於對輸入數據矩陣進行了2*2的均值下采樣,因此導致數據尺寸會縮小為原來的四分之一,即14*14。
(3)卷積層C3:輸入圖像尺寸為14*14,卷積核尺寸為5*5,輸入數據模板數量為6個,該層卷積模板種類為16個,導致C3層對每個輸入的圖像進行卷積操作之後,得到16個卷積特征模板輸出,並且卷積後圖像的尺寸變為14-5+1=10。並且C3層與S2層之間的連接屬性並非是默認的全連接,而是按照指定連接方式(存儲在connection變量中)進行連接。
(4)均值下采樣層S4:輸入數據矩陣的尺寸為10*10,輸入數據矩陣的個數為16個,均值下采樣的鄰域窗口為2*2,與S2相似,這裡的下采樣操作同樣導致矩陣尺寸減半,因此S4層的特征矩陣輸入尺寸為5*5。
(5)卷積層C5:輸入數據矩陣尺寸為5*5,卷積核尺寸為5*5,輸入數據模板數量為16,卷積核模板種類為120個。由於在這一層數據矩陣的尺寸已經和卷積核尺寸相同,導致每一次的卷積操作都將得到一個具體數值(即卷積窗口無法進行滑動),導致C5層輸出的特征結構是一個120維的特征向量。
(6)全連接層:輸入特征維數為120,輸出特征維數為10(一共有十類),完成特征的分類工作,類此與一個抽象的線性分類函數。
(6)激活函數:從代碼中可以看出,這裡各個層之間的激活函數統一選用tan_h函數,當然tiny_cnn中還封裝了很多其他類型的激活函數,在這裡可以隨便選擇,但需要注意的一點是這個網絡中理論上只能使用一種類型的激活函數。
二、partial_connected_layer類結構
在分析partial_connected_layer類的過程中,同樣遵循“成員變量-構造函數-功能函數”的分析流程
2.1 成員變量
partial_connected_layer類主要有以下五個成員變量:

這五個成員變量的結構及功能是分析tiny_cnn網絡映射機制的一個重點,因此在這裡對其著重進行一下分析。首先需要注明一點的是,前三個變量本質上是一個雙層vector結構的成員變量,之所以稱其為雙層vector,是因為在io_connection等別名對應的宏定義中,已經包含了一層vector屬性:

因此weight2io_、out2wi_、in2wo_、bias2out_均是雙層的vector結構,前三個變量的核心存儲單元是pair(,),第四個變量的核心存儲單元則是一個無符號整型變量,為了更好的說明這種雙層vector的特殊結構,這裡給出一個示意圖:
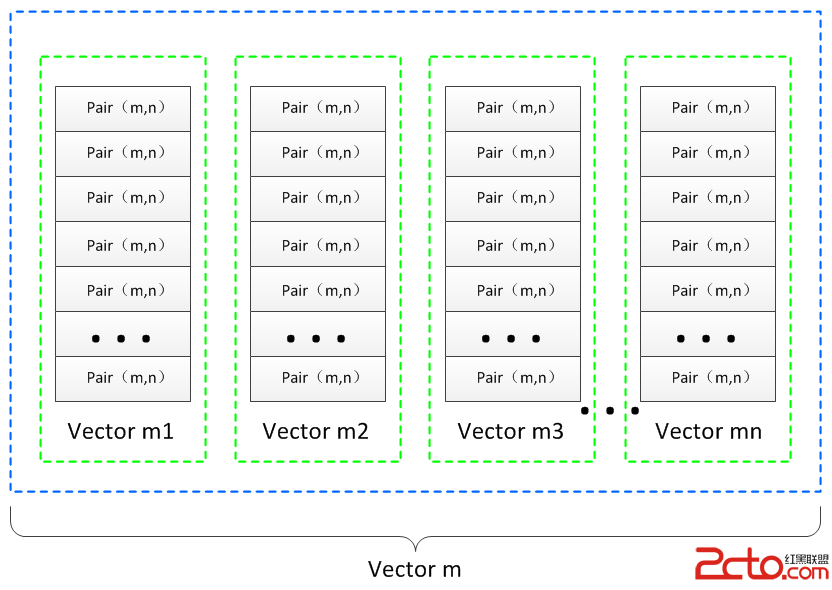
這裡之所以采用了雙層的vector結構,主要原因在於partial_connected_layer類是一個基類型,需要卷積層和下采樣層提供基本層結構框架,而在實際的網絡模型中都包含多個相同結構的卷積層和下采樣層,在對具體某一層的某一個映射核進行索引時,就需要用到這種雙層的vector結構。最外層的vector(vector m)用來標記當前層的具體標號,即指明當前層是具體哪一層;內層的vector()(vector m1~vector mn)用來索引當前層中具體哪一個卷積核,因為一個卷積核包含多個權重值(例如C1層共有6個卷積核,每個卷積核包含5*5=25個權重值,因此C1層在存儲卷積核權重時需要用到6個vecto類型容器,每個容器中包含25個值)。總之一個卷積核中包含多個權重值,一個卷積層中包含多個卷積核,這就要求使用一種雙層vector的數據結構對它進行存儲,其索引機制一定程度上有些類似於二維數組的索引機制。
OK,這篇博客就先介紹到這裡,在下一篇博文中我們將著重介紹partial_connected_layer類中的相關構造函數以及一些重要的功能函數。