二維平面上有n個點(xi, yi),現在這些點中取若干點構成一個集合S,對它們按照x坐標排序,順次連接,將會構成一些連續上升、下降的折線,設其數量為f(S)。如下圖中,1->2,2->3,3->5,5->6(數字為下圖中從左到右的點編號),將折線分為了4部分,每部分連續上升、下降。
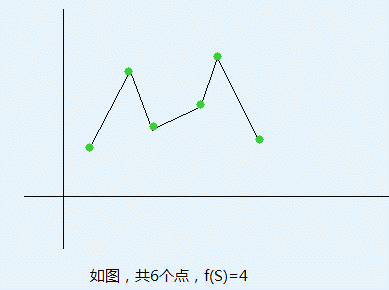
現給定k,求滿足f(S) = k的S集合個數。
Input
第一行兩個整數n和k,以下n行每行兩個數(xi, yi)表示第i個點的坐標。所有點的坐標值都在[1, 100000]內,且不存在兩個點,x坐標值相等或y坐標值相等
Output
輸出滿足要求的方案總數 mod 100007的結果
Sample Input
5 1
5 5
3 2
4 4
2 3
1 1
Sample Output
19
HINT
對於100%的數據,n <= 50000,0 < k <= 10
Source
首先我們將點按照x軸排序。
我們也可以將縱坐標離散化。
然後就可以用動態規劃解決了。
令f[i][j][0]和f[i][j][1]分別表示前i個點,選擇j段,最後一段是下降或者上升的方案數。
狀態轉移方程如下:
f[i][j][0]=∑(f[k][j][0]+f[k][j-1][1]) (ka[i].y)
f[i][j][1]=∑(f[k][j][1]+f[k][j-1][0]) (k
很明顯可以用樹狀數組或者線段樹優化。
#include
#include
#include
#include
#include
#include
#define F(i,j,n) for(int i=j;i<=n;i++)
#define D(i,j,n) for(int i=j;i>=n;i--)
#define ll long long
#define maxn 100005
#define mod 100007
using namespace std;
struct data{int x,y;}a[maxn];
int n,m,b[maxn];
inline int read()
{
int x=0,f=1;char ch=getchar();
while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
while (ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
inline bool cmp(data d1,data d2)
{
return d1.x
