LeetCode 204 Count Primes（質數計數）（*）

翻譯

計算小於一個非負整數n的質數的個數。

原文

Count the number of prime numbers less than a non-negative number, n.

分析

這道題以前遇到過，當時是用的最笨的辦法，現在也沒什麼好想法，又恰好題目有提示，我就點開了。題目的提示是一條一條給出來的，我也就逐個的全點開了，感覺好失敗……

public int countPrimes(int n) {
   int count = 0;
   for (int i = 1; i < n; i++) {
      if (isPrime(i)) count++;
   }
   return count;
}

private boolean isPrime(int num) {
   if (num <= 1) return false;
   // Loop's ending condition is i * i <= num instead of i <= sqrt(num)
   // to avoid repeatedly calling an expensive function sqrt().
   for (int i = 2; i * i <= num; i++) {
      if (num % i == 0) return false;
   }
   return true;
}

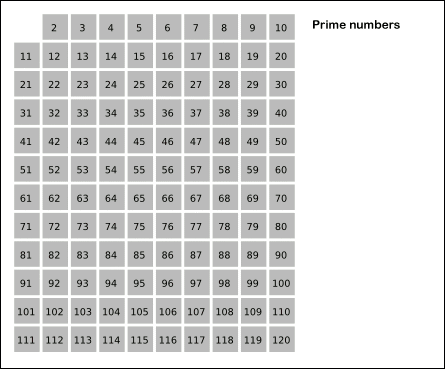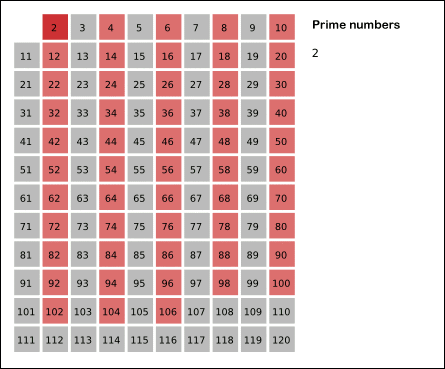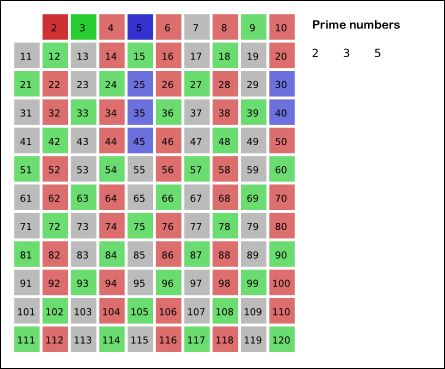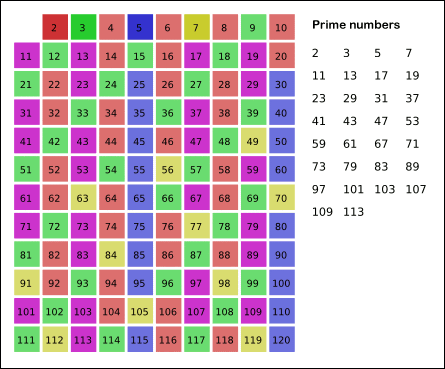
The Sieve of Eratosthenes is one of the most efficient ways to find all prime numbers up to n. 
I promise that the concept is surprisingly simple.

public int countPrimes(int n) {
   boolean[] isPrime = new boolean[n];
   for (int i = 2; i < n; i++) {
      isPrime[i] = true;
   }
   // Loop's ending condition is i * i < n instead of i < sqrt(n)
   // to avoid repeatedly calling an expensive function sqrt().
   for (int i = 2; i * i < n; i++) {
      if (!isPrime[i]) continue;
      for (int j = i * i; j < n; j += i) {
         isPrime[j] = false;
      }
   }
   int count = 0;
   for (int i = 2; i < n; i++) {
      if (isPrime[i]) count++;
   }
   return count;
}

以上均為LeetCode原文……

把上面的代碼翻譯一下成如下：

class Solution {
public:
    bool isPrime(int num) {
        if (num <= 1) return false;
        for (int i = 2; i*i <= num; ++i) {
            if (num%i == 0) return false;
        }
        return true;
    }

    int countPrimes(int n) {
        bool *isPrime = new bool[n];
        for (int i = 2; i < n; ++i) {
            isPrime[i] = true;
        }
        for (int i = 2; i*i < n; ++i) {
            if (!isPrime[i]) continue;
            for (int j = i*i; j < n; j += i) {
                isPrime[j] = false;
            }
        }
        int count = 0;
        for (int i = 2; i < n; ++i) {
            if (isPrime[i]) count++;
        }
        return count;
    }
};

摘錄一些代碼：

class Solution {
public:
    int countPrimes(int n) {
        switch(n) {
            case 0:
            case 1:
            case 2: return 0;
            case 3: return 1;
            case 4:
            case 5: return 2;
            case 6: 
            case 7: return 3;
            case 8:
            case 9: 
            case 10: 
            case 11: return 4;
            case 12: 
            case 13: return 5;
            case 14: 
            case 15: return 6;
            case 10000: return 1229;
            case 499979: return 41537;
            case 999983: return 78497;
            case 1500000: return 114155;
        }
    }
};

int countPrimes(int n) {
    if(--n < 2) return 0;
    int m = (n + 1)/2, count = m, k, u = (sqrt(n) - 1)/2;
    bool notPrime[m] = {0};

    for(int i = 1; i <= u;i++)
        if(!notPrime[i])
          for(k = (i+ 1)*2*i; k < m;k += i*2 + 1)
              if (!notPrime[k])
              {
                  notPrime[k] = true;
                  count--;
              }
    return count;
}