opencv小練習：哈爾小波(Haar)

首先說一下一維haar小波的原理。
例如我們有一個一維的圖像[2,4,6,8,10,12,14,16].

求均值：我們求相鄰像素的均值[3,7,11,15]。這個新的圖像分辨率就成了原來的一半(8/2=4)。

求差值。上面的均值我們存儲了圖像的整體信息。但是很多細節信息我們丟掉了，所以我們同時要記錄圖像的細節信息，這樣在重構時能夠恢復圖像的全部信息。下面是求第m個差值的公式：

b[m]=(a[2m]?a[2m+1])/2

經過計算我們得到了結果[-1,-1,-1,-1]。這個新的分辨率也成了原來的一半(8/2=4)。
3. 此時上面兩步形成了第一次分解的結果[3,7,11,15,-1,-1,-1,-1]。包含了圖像的整體信息和細節信息。接下來的分解我們重復1,2步，將整體信息再次進行分解，得到了二級分解結果[5，13，-2，-2].同樣的，前面的[5,13]是整體信息，後面的[-2,-2]是細節信息。

分辨率 整體信息 細節信息 4 3,7,11,15 -1,-1,-1,-1 2 5，13 -2，-2 1 9 -4

經過三次分解，我們得到了一個整體信息和三個細節系數，這個就是一維小波變換。

對於二維haar小波，我們通常一次分解形成了整體圖像，水平細節，垂直細節，對角細節。首先我們按照一維haar小波分解的原理，按照行順序對行進行處理，然後按照列順序對行處理結果進行同樣的處理。最後形成了如下的形式。

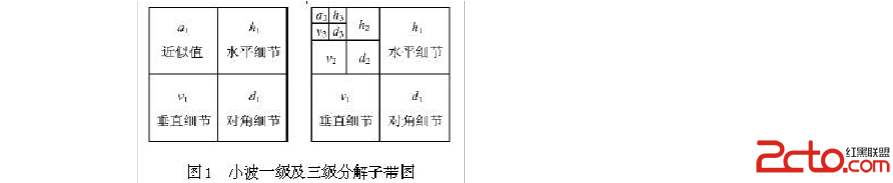
接下來就是代碼時間了，首先看下代碼結果:

c++代碼（Z喎?/kf/ware/vc/" target="_blank" class="keylink">vcGVuY3aw5rG+o7pvcGVuY3YzLjCjqaO6PC9wPg0KPHByZSBjbGFzcz0="brush:java;"> /************************************************* Copyright:zhuchen Author: zhuchen Date:2016-01-10 Description:多級haar小波變換 **************************************************/ # include # include using namespace std; using namespace cv; int main(){ Mat img = imread("lenna.bmp",0); int Height = img.cols; int Width = img.rows; int depth = 3; //定義分解深度 int depthcount = 1; Mat tmp = Mat::ones(Width, Height, CV_32FC1); Mat wavelet = Mat::ones(Width, Height, CV_32FC1); Mat imgtmp = img.clone(); imgtmp.convertTo(imgtmp, CV_32FC1); while (depthcount<=depth){ Width = img.rows / depthcount; Height = img.cols / depthcount; for (int i = 0; i < Width; i++){ for (int j = 0; j < Height / 2; j++){ tmp.at(i, j) = (imgtmp.at(i, 2 * j) + imgtmp.at(i, 2 * j + 1)) / 2; tmp.at(i, j + Height / 2) = (imgtmp.at(i, 2 * j) - imgtmp.at(i, 2 * j + 1)) / 2; } } for (int i = 0; i < Width / 2; i++){ for (int j = 0; j < Height; j++){ wavelet.at(i, j) = (tmp.at(2 * i, j) + tmp.at(2 * i + 1, j)) / 2; wavelet.at(i + Width / 2, j) = (tmp.at(2 * i, j) - tmp.at(2 * i + 1, j)) / 2; } } imgtmp = wavelet; depthcount++; } namedWindow("jpg",0); wavelet.convertTo(wavelet, CV_8UC1); wavelet += 50; //圖像暗度過低，所以這裡我加了50 imshow("jpg", wavelet); waitKey(0); return 0; }