leetcode筆記：Largest Rectangle in Histogram

一.題目描述

Given n non-negative integers representing the histogram’s bar height where the width of each bar is 1, find the area of largest rectangle in the histogram.

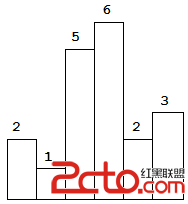
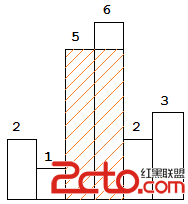
Above is a histogram where width of each bar is 1, given height =[2,1,5,6,2,3].

vcPmu/08Y29kZT4xICogNiA9IDY8L2NvZGU+oaOyu7bPuPzQwrXDtb21xNfutPPD5rv9o6zX7rrzt7W72LjD1rW8tL/JoaPV4tbWt723qLXEyrG85Li01NO2yM6qPGNvZGU+TyhuXjIpPC9jb2RlPqOsu+GzrMqxoaM8L3A+DQo8cD7V/ci3tvi439CntcS3vbeoysfN+MnPueO3uszWwtu1xNK71ta3vbeoo6y96Nb61bvAtMq1z9bL47eoo6y1q8rHuMPL47eosqKyu8jd0tfC7cnPz+u1vaGj1eLA77LOv7zBy9K7uPa88rWltcTA/dfTwLTLtcP3tMvL47eoo7o8L3A+DQo8cD48aW1nIGFsdD0="這裡寫圖片描述" src="/uploadfile/Collfiles/20151014/2015101408345790.png" title="\" />

圖中，height = [5,6,7,8,3]，特點是除了最後一個，前面全部保持遞增，且最後一個立柱的高度小於前面所有立柱高度。

對於這種特點的柱狀圖，我們知道除了最後一個，從第一個到倒數第二個立柱的高度都在升高，如果挨個使用每一個柱的高度作為矩形的高度，那麼依次能得到的矩形的寬度就可以直接算出來：使用5作為高度可以使用前四個立柱組成 4*5的矩形，同理使用高度6 的立柱可以組成3*6的矩形…… 因此只需要遍歷一次height，就可以計算出最大面積，也就是時間復雜度O(n)。

參考博文中，將這種特點的柱狀圖稱為“波峰圖”。

下面介紹算法的具體步驟：

1.在height數組的尾部添加0，其作用是得到符合上述規律的直方圖。

2.定義了一個棧k，遍歷數組height，時如果height[index]大於stack.top()，入棧；反之則出棧，直到棧頂元素小於height[index]。由於出棧的這些元素高度都是遞增的，我們可以依次求出這些立柱中所圍成的矩形面積，並更新其最大值。

3.重復以上過程，直到遍歷到最後那個值0的元素，會把棧中元素全部彈出並作最後一次面積的計算，並返回面積的最大值。

注意棧中存的不是height元素的大小，而是height的索引，這樣做的好處是不會影響寬度的計算，當前遍歷的索引值 - 當前棧頂索引值 - 1 = 當前矩形的寬度。

三.示例代碼

class Solution
{
public:
    int largestRectangleArea(vector &height)
    {
        if (height.size() == 0) return 0;
        height.push_back(0);
        int MaxHist = 0;  // 存儲最大矩形面積
        stack k;     // 使用棧存儲height的索引

        for (int index = 0; index < height.size(); ++index)
        {
            if (k.empty() || height[k.top()] < height[index]) 
                k.push(index);
            else
            {
                int temp = k.top();
                k.pop();
                // 局部面積計算，寬度為當前index與棧頂存儲的索引k.top()的距離
                int localArea = height[temp] * (k.empty() ? index : (index - k.top() - 1)); 
                if (localArea > MaxHist)
                    MaxHist = localArea;
                --index;
            }
        }
        return MaxHist;
    }
};

四.小結

該題目要求遍歷每一個立柱並將其視為矩形高度，求出直方圖中能構成矩形的最大面積，但是它通過巧妙地使用棧，把整個height變成一組組“波峰圖”來求解，做到了O(n)的時間復雜度，值得深入學習！