leetcode筆記：Climbing Stairs（斐波那契數列問題）

一.題目描述

You are climbing a stair case. It takes n steps to reach to the top.
Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top?

題目的大意是，已知有n階樓梯，每次只能爬1階或2階樓梯，問爬到第n階樓梯共有幾種爬法-_-||。題目可以看成是，設f(n)表示爬到第n 階樓梯的方法數，為了爬到第n階樓梯，有以下兩種選擇：
• 從第f(n-1)階前進1步；
• 從第f(n-2)階前進2步；
則f(n)可寫成：f(n) = f(n-1) + f(n-2)

題目轉化為斐波那契數列的問題，關於這一內容，網上相關研究有很多，概念傳送門：
http://baike.baidu.com/link?url=c2Bmk2jBGbI46qTIA-qKmdTkYBrVYYrejAHzf8BJRwCekIL4Sbx48fFCRkeGdul0

二.題目分析

關於斐波那契序列，可以使用遞歸或者迭代來解決問題，該書列可寫成以下遞推關系：

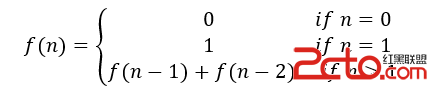
顯然，使用遞推關系式反復迭代並不是最優的解法，在計算f(n)值時，需要計算f(1),f(2),…,f(n-1)的所有值，其中存在很多重復的運算，如計算f(4)=f(3)+f(2)，其中需要求解f(3)=f(2)+f(1)。若使用一個數組用於儲存所有計算過的項，可以把時間復雜度降至O(n)，而空間復雜度也為O(n)。

這裡為了追求時間復雜度，因此直接使用斐波那契的通項公式，該公式的推導過程如下：

三.示例代碼

#include 
using namespace std;

class Solution
{
public:
    // 時間復雜度O(1)
    int climbStairs1(const int n)
    {
        const double sqrtNum = sqrt(5);
        return int(floor((pow((1 + sqrtNum) / 2, n + 1) - pow((1 - sqrtNum) / 2, n + 1)) / sqrtNum));
    }

    // 時間復雜度O(n)
    int climbStairs2(const int n)
    {
        int current = 1;
        int last = 0;
        for (int i = 1; i <= n; i++)
        {
            int temp = current;
            current += last;
            last = temp;
        }
        return current;
    }
};

簡單的測試代碼：

#include ClimbingStairs.h
#include 

int main()
{
    int n;
    cout << How many stairs?  << Input: ;
    cin >> n;
    Solution s;
    int result1 = s.climbStairs1(n);
    int result2 = s.climbStairs2(n);

    cout << How many ways to reach the finish line?  Result1： << result1 << endl;
    cout << How many ways to reach the finish line?  Result2： << result2 << endl;
    system(pause);
    return 0;
}

漏洞，因為通項公式使用浮點運算，還出現了物理書，因此不能保證結果的精度。而在《編程之美》一書中，還給出一種分治策略的解決方法。該算法可做到時間復雜度O(Log2n)，而網上更有博文寫出了七種解斐波那契序列的方法，還要繼續深入研究啊。