程式師世界 >> 編程語言 >> C語言 >> C++ >> 關於C++ >> hdu5375 Gray code(動態規劃)

hdu5375 Gray code(動態規劃)

編輯：關於C++

題目：

Gray code

Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 860 Accepted Submission(s): 490

Problem Description The reflected binary code, also known as Gray code after Frank Gray, is a binary numeral system where two successive values differ in only onebit (binary digit). The reflected binary code was originally designed to prevent spurious output from electromechanical switches. Today, Gray codes are widely used to facilitate error correction in digital communications such as digital terrestrial television and some cable TV systems.

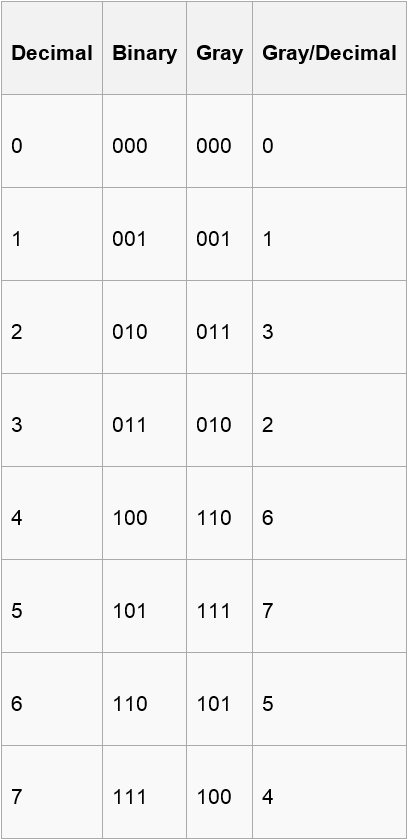
Now , you are given a binary number of length n including ‘0’ , ’1’ and ‘?’(? means that you can use either 0 or 1 to fill this position) and n integers(a1,a2,….,an) . A certain binary number corresponds to a gray code only. If the ith bit of this gray code is 1,you can get the point ai.
Can you tell me how many points you can get at most?

For instance, the binary number “00?0” may be “0000” or “0010”,and the corresponding gray code are “0000” or “0011”.You can choose “0000” getting nothing or “0011” getting the point a3 and a4.

Input The first line of the input contains the number of test cases T.

Each test case begins with string with ‘0’,’1’ and ‘?’.

The next line contains n (1<=n<=200000) integers (n is the length of the string).

a1 a2 a3 … an (1<=ai<=1000)

Output For each test case, output “Case #x: ans”, in which x is the case number counted from one,’ans’ is the points you can get at most
Sample Input

Sample Output

Case #1: 12
Case #2: 15
Hint
https://en.wikipedia.org/wiki/Gray_code

http://baike.baidu.com/view/358724.htm

Author UESTC
Source 2015 Multi-University Training Contest 7
Recommend wange2014

題意：給一個n位二進制數，有一些位告訴了，有一些位不確定，把它轉化為格雷碼後為1的位置獲得對應位置的分數，問最多得多少分。

思路：二進制轉格雷碼的公式為G[0]=B[0],G[i]=B[i]^B[i-1]，所以當二進制第i位取值和第i-1位取值不同時，G[i]=1，可以得到A[i],否則G[i]=0,不能得到分數，DP方程為dp[i][0]=max(dp[i-1][0],dp[i-1][1]+a[i]),dp[i][1]=max(dp[i-1][1],dp[i-1][0]+a[i]),最終的結果為max(dp[n-1][1],dp[n-1][0]).

代碼：

#include 
#include 
#include 
#include 
#include 
#include
#include 
#include 
#include 
#include 
#include 
#include
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;

#define PB push_back
#define MP make_pair

#define REP(i,x,n) for(int i=x;i<(n);++i)
#define FOR(i,l,h) for(int i=(l);i<=(h);++i)
#define FORD(i,h,l) for(int i=(h);i>=(l);--i)
#define SZ(X) ((int)(X).size())
#define ALL(X) (X).begin(), (X).end()
#define RI(X) scanf(%d, &(X))
#define RII(X, Y) scanf(%d%d, &(X), &(Y))
#define RIII(X, Y, Z) scanf(%d%d%d, &(X), &(Y), &(Z))
#define DRI(X) int (X); scanf(%d, &X)
#define DRII(X, Y) int X, Y; scanf(%d%d, &X, &Y)
#define DRIII(X, Y, Z) int X, Y, Z; scanf(%d%d%d, &X, &Y, &Z)
#define OI(X) printf(%d,X);
#define RS(X) scanf(%s, (X))
#define MS0(X) memset((X), 0, sizeof((X)))
#define MS1(X) memset((X), -1, sizeof((X)))
#define LEN(X) strlen(X)
#define F first
#define S second
#define Swap(a, b) (a ^= b, b ^= a, a ^= b)
#define Dpoint  strcut node{int x,y}
#define cmpd int cmp(const int &a,const int &b){return a>b;}

 /*#ifdef HOME
    freopen(in.txt,r,stdin);
    #endif*/
const int MOD = 1e9+7;
typedef vector VI;
typedef vector VS;
typedef vector VD;
typedef long long LL;
typedef pair PII;
//#define HOME

int Scan()
{
	int res = 0, ch, flag = 0;

	if((ch = getchar()) == '-')				//判斷正負
		flag = 1;

	else if(ch >= '0' && ch <= '9')			//得到完整的數
		res = ch - '0';
	while((ch = getchar()) >= '0' && ch <= '9' )
		res = res * 10 + ch - '0';

	return flag ? -res : res;
}
/*----------------PLEASE-----DO-----NOT-----HACK-----ME--------------------*/



char str[200000+5];
int a[200000+5];
 int dp[200000][2];
int main()
{int T;
RI(T);
for(int t=1;t<=T;t++)
{
    scanf(%s,str);
    int n=strlen(str);
    for(int i=0;i