程式師世界 >> 編程語言 >> C語言 >> C++ >> 關於C++ >> HDU 5407 CRB and Candies（數論+yy）

HDU 5407 CRB and Candies（數論+yy）

編輯：關於C++

HDU 5407

題意：

計算：
LCM(C0N,C1N,C2N,...,CNN)(1<=N<=106)

思路：

先打個表看看？
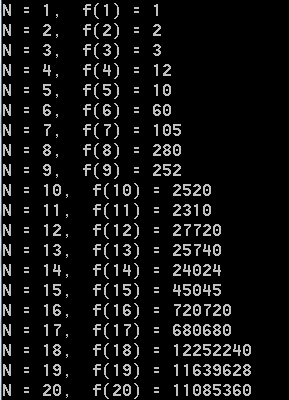
這裡寫圖片描述
我們可以發現:
f(3)=f(4)/4,f(5)=f(6)/6,
f(9)=f(10)/10,f(11)=f(12)/12
f(15)=f(16)/16,f(17)=f(18)/18
這個迷之規律會在什麼時候出現呢？“遠離”單個素數冪的時候。
而素數冪會對什麼造成影響呢？結合題目，應該是前n個數的LCM。
所以，規律就是
f(n)=LCM(1,2,3,4,5,..,n+1)n+1
這裡放上嚴格證明：
(http://www.zhihu.com/question/34859879/answer/60168919)
那麼如何計算f(n)呢？
我們設g(n)=LCM(1,2,3,..,n)
如果 n=pk,g(n)=g(n−1)∗p.
否則 g(n)=g(n−1).
所以我們可以先篩出素數表，然後預處理出g(n)，然後便可在O(1)的時間內實現查詢。
計算f(n)的時候不能直接除以(n+1)，應乘以其逆元.
總復雜度：
預處理：
篩素數 + 求g(n) ：O(nlogn)
查詢：O(1)。<喎?/kf/ware/vc/" target="_blank" class="keylink">vcD4NCjxoMyBpZD0="代碼">代碼：

/*
* @author FreeWifi_novicer
* language : C++/C
*/
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include

using namespace std;

#define clr( x , y ) memset(x,y,sizeof(x))
#define cls( x ) memset(x,0,sizeof(x))
#define mp make_pair
#define pb push_back
typedef long long lint;
typedef long long ll;
typedef long long LL;
const int maxn = 1000000 + 10 ;
bool isprime[maxn] ;
lint lcm[maxn] ;
lint f[maxn] ;
vectorp ;
const int mod = 1e9 + 7 ;
void sieve(){
    clr( isprime , true ) ;
    for( lint i = 2 ; i * i <= maxn ; i++ ){
        if( isprime[i] )
            for( lint j = i * i ; j <= maxn ; j += i )
                isprime[j] = false ;
    }
    for( lint i = 2 ; i <= maxn ; i++ )
        if( isprime[i] )
            p.pb( i ) ;
}

void init_lcm(){
    sieve() ;
    vector:: iterator it ;
    for( lint i = 1 ; i <= maxn ; i++ ) lcm[i] = 1 ;
    for( it = p.begin() ; it != p.end() ; it++ ){
        for( lint j = *it ; j <= maxn ; j = *it * j ){
            lcm[j] = *it ;
        }
    }
    f[1] = 1 ;
    for( lint i = 2 ; i <= maxn ; i++ ) f[i] = f[i-1] * lcm[i] % mod ;
}

lint fast_pow( lint x , lint n ){
    lint res = 1 ;
    while( n ){
        if( n & 1 )
            res = res * x % mod ;
        n >>= 1 ;
        x = x * x % mod ;
    }
    return res ;
}
void solve( lint n ){
    n++;
    lint x = fast_pow( n , mod - 2 ) ;
    lint ans = f[n] * x % mod ;
    cout << ans << endl;
}
int main(){
//  freopen(input.txt,r,stdin);
    int t ; cin >> t ;
    init_lcm() ;
    while( t-- ){
        lint n ;
        cin >> n ;
        solve( n ) ;
    }
    return 0;
}