Gray code

Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 330 Accepted Submission(s): 183


Problem Description The reflected binary code, also known as Gray code after Frank Gray, is a binary numeral system where two successive values differ in only onebit (binary digit). The reflected binary code was originally designed to prevent spurious output from electromechanical switches. Today, Gray codes are widely used to facilitate error correction in digital communications such as digital terrestrial television and some cable TV systems.



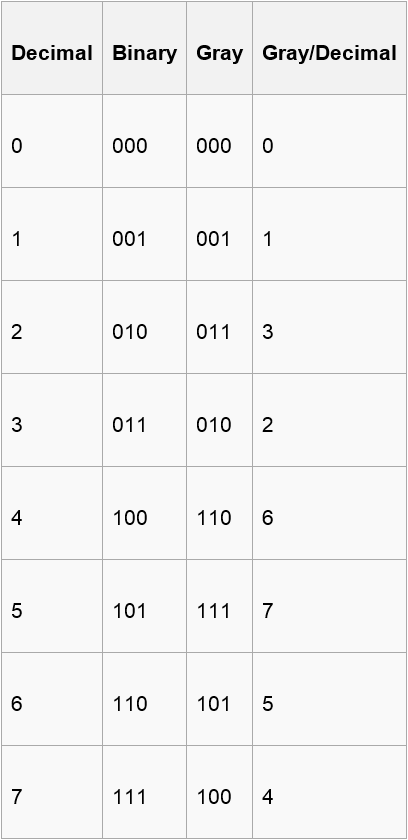
Now , you are given a binary number of length n including ‘0’ , ’1’ and ‘?’(? means that you can use either 0 or 1 to fill this position) and n integers(a1,a2,….,an) . A certain binary number corresponds to a gray code only. If the ith bit of this gray code is 1,you can get the point ai.
Can you tell me how many points you can get at most?

For instance, the binary number “00?0” may be “0000” or “0010”,and the corresponding gray code are “0000” or “0011”.You can choose “0000” getting nothing or “0011” getting the point a3 and a4.

Input The first line of the input contains the number of test cases T.

Each test case begins with string with ‘0’,’1’ and ‘?’.

The next line contains n (1<=n<=200000) integers (n is the length of the string).

a1 a2 a3 … an (1<=ai<=1000)

Output For each test case, output “Case #x: ans”, in which x is the case number counted from one,’ans’ is the points you can get at most
Sample Input

2
00?0
1 2 4 8
????
1 2 4 8

Sample Output

Case #1: 12
Case #2: 15
Hint
https://en.wikipedia.org/wiki/Gray_code

http://baike.baidu.com/view/358724.htm
 

Source 2015 Multi-University Training Contest 7

 

 

格雷碼：是由二進制當前位對前以為異或得到的；

eg：二進制 (0)10011

格雷碼 11010 即：0^1=1; 1^0=1; 0^0=0; 0^1=1; 1^1=0;

 

所以：有 (0)x???y 和 (0)x??y

當x,y不是'?'

當x==y的時候：如果xy之間的?是奇數個那麼把x後面的值到y都加起來a[i],(x

那麼如果是偶數個呢，那就把和減去min(a[i]),(x

eg: 0????0 那麼我們應該讓串為：010010 ----->對應格雷碼：010111

a[i]= 5 4 2 1 3 6 所以sum=4+2+3+6=15;

當x!=y的時候：如果xy之間的?是偶數個那麼把x後面的值到y都加起來a[i],(x

那麼如果是奇數個呢，那就把和減去min(a[i]),(x

eg: 0???1 那麼我們應該讓串為：01101 ----->對應格雷碼：01011

a[i]= 5 4 1 2 3 所以sum=4+2+3=9;

等於'?'相當於上述情況，你可以在首位加(0);

 

 

#include 
#include
#include
using namespace std;
#define N 200005
#define LL long long

int t,len,a[N],ca=1;
char str[N];

int main()
{
//    freopen(a.txt,r,stdin);
    scanf(%d,&t);
    while(ca<=t)
    {
        scanf(%s,str+1);
        len=strlen(str+1);
        a[0]=0;
        for(int i=1;i<=len;i++)
        {
            scanf(%d,&a[i]);
        }
        int flag=0,s1,s2,sa=0;
        LL sum=0;
        str[0]='0';
        char st='0',en;
        for(int i=1;i<=len;i++)
        {

            if(str[i]!='?')
            {
                en=str[i];
                s2=a[i];

                if(sa>0)
                {
                    sum+=s2;
                    if(sa&1 && st!=en) sum-=min(s1,s2);
                    else if(sa%2==0 && st==en) sum-=min(s1,s2);
                }
                sa=0;
                st=str[i];
                if(str[i-1]!='?' && str[i]^str[i-1])
                    sum+=a[i];
            }
            else
            {
                sa++;

                sum+=a[i];
                if(sa==1) s1=a[i];
                else s1=min(s1,a[i]);

            }
        }
        printf(Case #%d: %lld
,ca++,sum);
    }
    return 0;
}

 

 

 

 

##1007. Gray code

格雷碼 題解 標准格雷碼的性質：二進制a1 a2 ... an，對應的格雷碼為a1 （a1 xor a2） ... （an-1 xor an） 題目就可以轉為O(n)的dp dp[i][j]表示二進制第i位為j時前i位對應最大分數.

當然dp就不要考慮這麼多了：

 

 

#include 
#include 
#include 
#include 
#include 
#include