hihoCoder_#1067_最近公共祖先·二(LCA模板)

#1067 : 最近公共祖先·二

描述

上上回說到，小Hi和小Ho用非常拙劣——或者說粗糙的手段山寨出了一個神奇的網站，這個網站可以計算出某兩個人的所有共同祖先中輩分最低的一個是誰。遠在美國的他們利用了一些奇妙的技術獲得了國內許多人的相關信息，並且搭建了一個小小的網站來應付來自四面八方的請求。

但正如我們所能想象到的……這樣一個簡單的算法並不能支撐住非常大的訪問量，所以擺在小Hi和小Ho面前的無非兩種選擇：

其一是購買更為昂貴的服務器，通過提高計算機性能的方式來滿足需求——但小Hi和小Ho並沒有那麼多的錢；其二則是改進他們的算法，通過提高計算機性能的利用率來滿足需求——這個主意似乎聽起來更加靠譜。

於是為了他們第一個在線產品的順利運作，小Hi決定對小Ho進行緊急訓練——好好的修改一番他們的算法。

而為了更好的向小Ho講述這個問題，小Hi將這個問題抽象成了這個樣子：假設現小Ho現在知道了N對父子關系——父親和兒子的名字，並且這N對父子關系中涉及的所有人都擁有一個共同的祖先（這個祖先出現在這N對父子關系中），他需要對於小Hi的若干次提問——每次提問為兩個人的名字（這兩個人的名字在之前的父子關系中出現過），告訴小Hi這兩個人的所有共同祖先中輩分最低的一個是誰？

輸入

每個測試點（輸入文件）有且僅有一組測試數據。

每組測試數據的第1行為一個整數N，意義如前文所述。

每組測試數據的第2~N+1行，每行分別描述一對父子關系，其中第i+1行為兩個由大小寫字母組成的字符串Father_i, Son_i，分別表示父親的名字和兒子的名字。

每組測試數據的第N+2行為一個整數M，表示小Hi總共詢問的次數。

每組測試數據的第N+3~N+M+2行，每行分別描述一個詢問，其中第N+i+2行為兩個由大小寫字母組成的字符串Name1_i, Name2_i，分別表示小Hi詢問中的兩個名字。

對於100%的數據，滿足N<=10^5，M<=10^5, 且數據中所有涉及的人物中不存在兩個名字相同的人（即姓名唯一的確定了一個人），所有詢問中出現過的名字均在之前所描述的N對父子關系中出現過，第一個出現的名字所確定的人是其他所有人的公共祖先。

輸出

對於每組測試數據，對於每個小Hi的詢問，按照在輸入中出現的順序，各輸出一行，表示查詢的結果：他們的所有共同祖先中輩分最低的一個人的名字。

樣例輸入

4
Adam Sam
Sam Joey
Sam Micheal
Adam Kevin
3
Sam Sam
Adam Sam
Micheal Kevin

樣例輸出

Sam
Adam
Adam

 

分析：裸的LCA離線算法。留作模板。

轉自：http://taop.marchtea.com/04.04.html

 

Tarjan算法 （以發現者Robert Tarjan命名）是一個在圖中尋找強連通分量的算法。算法的基本思想為：任選一結點開始進行深度優先搜索dfs（若深度優先搜索結束後仍有未訪問的結點，則再從中任選一點再次進行）。搜索過程中已訪問的結點不再訪問。搜索樹的若干子樹構成了圖的強連通分量。

應用到咱們要解決的LCA問題上，則是：對於新搜索到的一個結點u，先創建由u構成的集合，再對u的每顆子樹進行搜索，每搜索完一棵子樹，這時候子樹中所有的結點的最近公共祖先就是u了。

 

引用一個例子，如下圖（不同顏色的結點相當於不同的集合）：

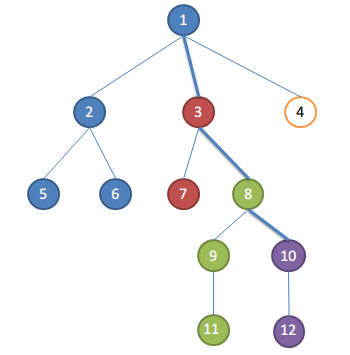
假設遍歷完10的孩子,要處理關於10的請求了，取根節點到當前正在遍歷的節點的路徑為關鍵路徑,即1-3-8-10，集合的祖先便是關鍵路徑上距離集合最近的點。

比如：

1，2，5，6為一個集合,祖先為1，集合中點和10的LCA為1 3，7為一個集合，祖先為3，集合中點和10的LCA為3 8，9，11為一個集合，祖先為8，集合中點和10的LCA為8 10，12為一個集合，祖先為10，集合中點和10的LCA為10

得出的結論便是：LCA(u,v)便是根至u的路徑上到節點v最近的點。

但關鍵是 Tarjan算法是怎麼想出來的呢？再給定下圖，你是否能看出來：分別從結點1的左右子樹當中，任取一個結點，設為u、v，這兩個任意結點u、v的最近公共祖先都為1。

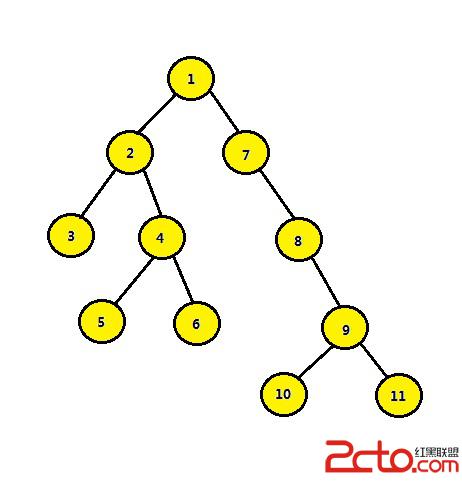
於此，我們可以得知：若兩個結點u、v分別分布於某節點t 的左右子樹，那麼此節點 t即為u和v的最近公共祖先。更進一步，考慮到一個節點自己就是LCA的情況，得知：

若某結點t 是兩結點u、v的祖先之一，且這兩結點並不分布於該結點t 的一棵子樹中，而是分別在結點t 的左子樹、右子樹中，那麼該結點t 即為兩結點u、v的最近公共祖先。

這個定理就是Tarjan算法的基礎。

如果要求多個任意兩個結點的最近公共祖先，則相當於是批量查詢。即在很多組的詢問的情況下，或許可以先確定一個LCA。例如是根節點1，然後再去檢查所有詢問，看是否滿足剛才的定理，不滿足就忽視，滿足就賦值，全部弄完，再去假設2號節點是LCA，再去訪問一遍。

可此方法需要判斷一個結點是在左子樹、還是右子樹，或是都不在，都只能遍歷一棵樹，而多次遍歷的代價實在是太大了，所以我們需要找到更好的方法。這就引出了下面要闡述的Tarjan算法，即每個結點只遍歷一次，怎麼做到的呢，請看下文講解。

Tarjan算法流程為：

 

Procedure dfs（u）；
    begin
        設置u號節點的祖先為u
        若u的左子樹不為空，dfs（u - 左子樹）；
        若u的右子樹不為空，dfs（u - 右子樹）；
        訪問每一條與u相關的詢問u、v
            -若v已經被訪問過，則輸出v當前的祖先t（t即u,v的LCA）
        標記u為已經訪問，將所有u的孩子包括u本身的祖先改為u的父親
    end

普通的dfs 不能直接解決LCA問題，故Tarjan算法的原理是dfs + 並查集 ，它每次把兩個結點對的最近公共祖先的查詢保存起來，然後dfs 更新一次。如此，利用並查集優越的時空復雜度，此算法的時間復雜度可以縮小至O(n＋Q)，其中，n為數據規模，Q為詢問個數。

 

 

i) 訪問1的左子樹

 

STEP 1：從根結點1開始，開始訪問結點1、2、3

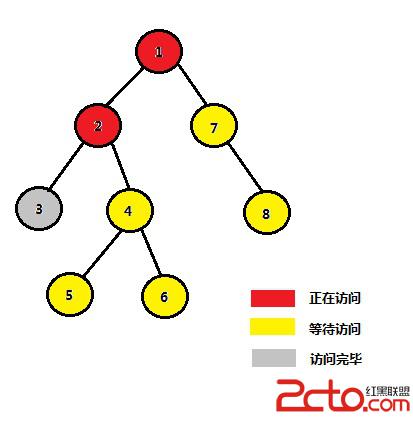
STEP 2：2的左子樹結點3訪問完畢

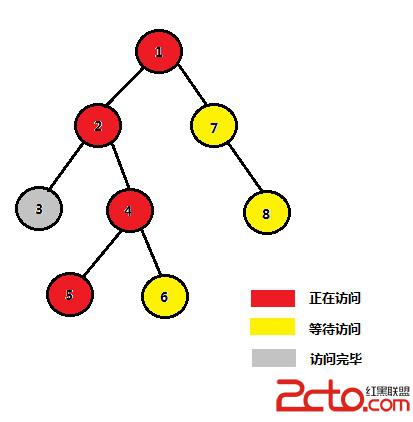
STEP 3：開始訪問2的右子樹中的結點4、5、6

STEP 4：4的左子樹中的結點5訪問完畢

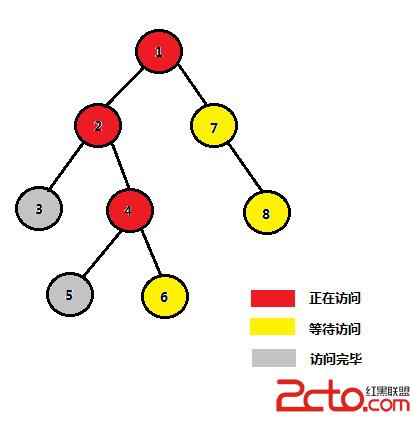
STEP 5：開始訪問4的右子樹的結點6

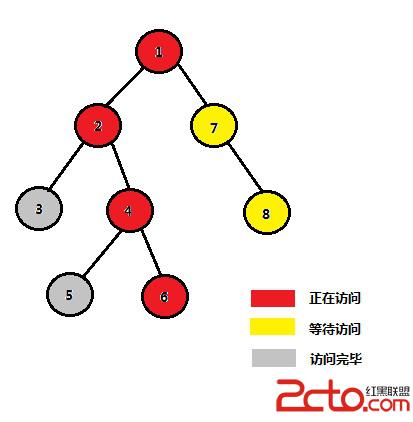
STEP 6：結點4的左、右子樹均訪問完畢，故4、5、6中任意兩個結點的LCA均為4

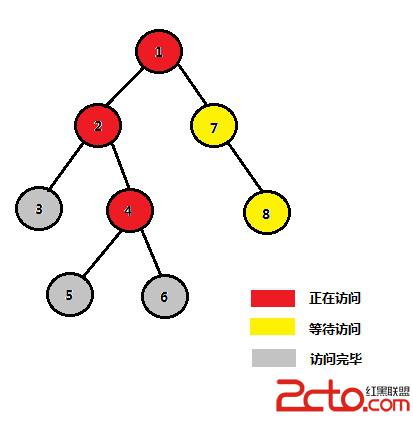
STEP 7：2的左子樹、右子樹均訪問完畢，故2、3、4、5、6任意兩個結點的LCA均為2

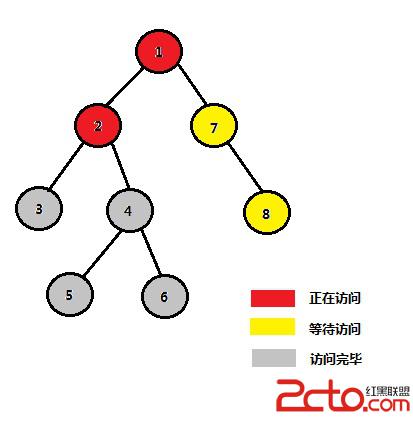
如上所述：進行到此step7，當訪問完結點2的左子樹（3），和右子樹（4、5、6）後，結點2、3、4、5、6這5個結點中，任意兩個結點的最近公共祖先均為2。

ii) 訪問1的右子樹

STEP 8：1的左子樹訪問完畢，開始訪問1的右子樹

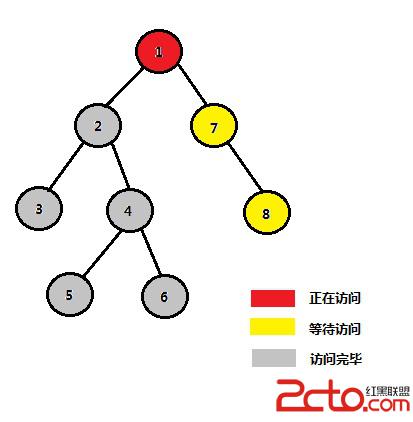
STEP 9：開始訪問1的右子樹中的結點7、8

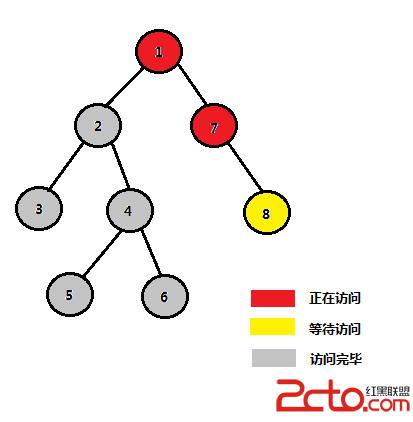
STEP 10

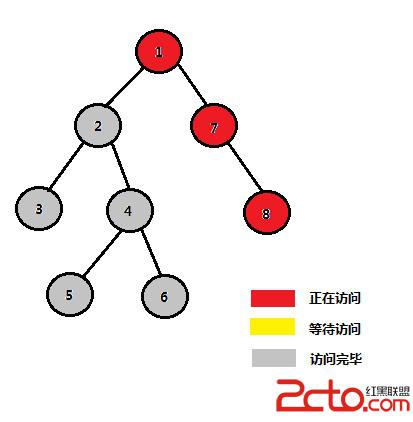
STEP 11

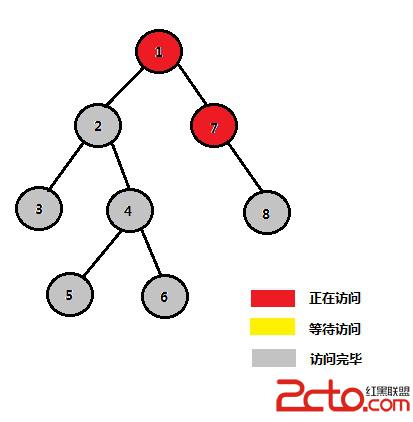
STEP 12：1的右子樹中的結點7、8訪問完畢

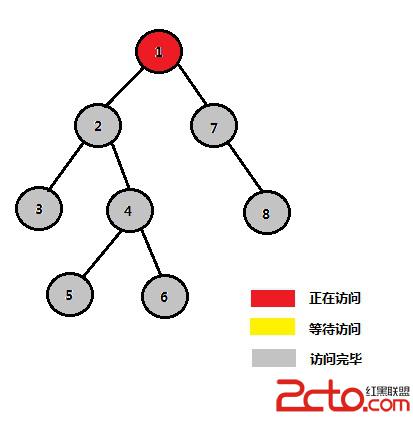
當進行到此step12，訪問完1的左子樹（2、3、4、5、6），和右子樹（7、8）後，結點2、3、4、5、6、7、8這7個結點中任意兩個結點的最近公共祖先均為1。

STEP 13：1的左子樹、右子樹均訪問完畢

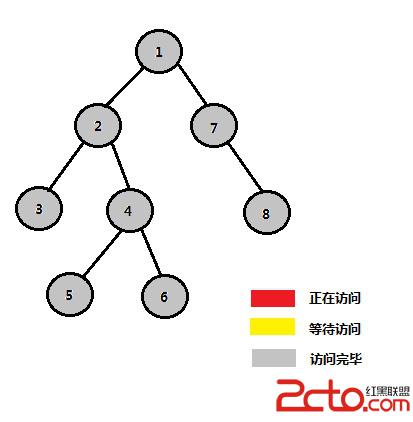
通過上述例子，我們能看到，使用此Tarjan算法能解決咱們的LCA問題。

 

代碼清單：

 

#include