Tri Tiling

Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 2731 Accepted Submission(s): 1547

 

Problem Description In how many ways can you tile a 3xn rectangle with 2x1 dominoes? Here is a sample tiling of a 3x12 rectangle.



Input Input consists of several test cases followed by a line containing -1. Each test case is a line containing an integer 0 ≤ n ≤ 30.

Output For each test case, output one integer number giving the number of possible tilings.

Sample Input

2
8
12
-1

Sample Output

3
153
2131

Source University of Waterloo Local Contest 2005.09.24

思路：

1.標記和概念說明

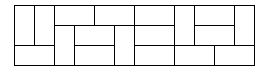
f(n):其中的n即為題目中矩形的長，高固定位3，也即為題目中說的3xn中的n，f(n)表示當長為n時，所有的擺放方式的數量。分割線:一條豎直的線，這條線穿過題目中的矩形，將矩形一分為二，且這條線不能從磚的中間穿過，也 就是說只有磚的邊緣對齊的時候，才能穿過。

2.解題思想

2.1 對於每一種磚的擺放情況，可能有多條上面說的分割線，但是對於每一種情況，我們只需要所有分割線中最右邊的一條，我們記為L。也就是說在L的右邊的部分就是不可分割的了，但是左邊可能還是可以分割的。對於L的左邊我們繼續使用函數f即可，而右邊是需要我們研究的主要部分，因為右邊不能應用函數f。

2.2 不能應用函數f的原因是因為右邊不在可分割。對於長度為2的不可分割矩形的擺放方式有三種方式，對長度大於2的不可分割矩形的擺放方式有兩種方式。上一句話的理解也許需要你拿起筆在紙上畫一畫。

2.3 同時，考慮這樣的L可能在哪些位置？可能在從右邊數起的長度為2的位置，也有可能在長度為4的位置，……， 也有可能在長度為n的位置。當然，也只可能在上述的位置中，

因此有如下結果：

f(n)=f(n-2)*3+f(n-4)*2+...+f(2)*2+f(0)*2 ---- 表達式1

然後，將上式用n-2替換得： f(n-2)=f(n-4)*3+f(n-6)*2+...+f(2)*2+f(0)*2 ---- 表達式2

表達式1減去表達式2得： f(n)=4*f(n-2)-f(n-4)2.4 在利用上面的遞推公式時，我們需要兩個遞推的出口，即f(0) = 1, f(2) = 3.由上面的遞推公式也知道 不涉及當n為奇數的情況，當n為奇數時，直接為零。因為當n為奇數時，矩形的面積為奇數，但是不管我們使 用了多少塊磚，磚的總面積一定是個偶數，所以不存在任何的擺放形式。
 
 

這裡有一點我覺得比較坑。那就是F[0]=1;當n=0的時候為什麼是1 ？？？

 

#include
#define LL __int64
LL ans[35];
void init()
{
    ans[0]=1;
    ans[1]=ans[3]=0;
    ans[2]=3;ans[4]=11;
    for(int i=5;i<=30;i++)
    {
        if(i&1) ans[i]=0;
        else ans[i]=ans[i-2]*4-ans[i-4];
    }
}
int main()
{
    int n;
    init();
    while(scanf(%d,&n)!=EOF)
    {
        if(n==-1) break;
        printf(%I64d
,ans[n]);
    }
    return 0;
}