Beans

Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)

Total Submission(s): 3521 Accepted Submission(s): 1681

 

Problem Description

Bean-eating is an interesting game, everyone owns an M*N matrix, which is filled with different qualities beans. Meantime, there is only one bean in any 1*1 grid. Now you want to eat the beans and collect the qualities, but everyone must obey by the following rules: if you eat the bean at the coordinate(x, y), you can’t eat the beans anyway at the coordinates listed (if exiting): (x, y-1), (x, y+1), and the both rows whose abscissas are x-1 and x+1.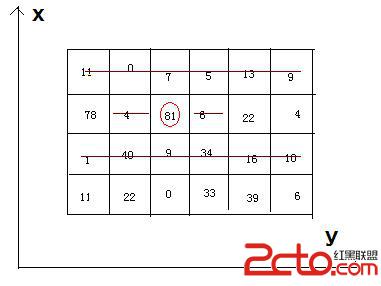


Now, how much qualities can you eat and then get ? Input There are a few cases. In each case, there are two integer M (row number) and N (column number). The next M lines each contain N integers, representing the qualities of the beans. We can make sure that the quality of bean isn't beyond 1000, and 1<=M*N<=200000. Output For each case, you just output the MAX qualities you can eat and then get. Sample Input

4 6
11 0 7 5 13 9
78 4 81 6 22 4
1 40 9 34 16 10
11 22 0 33 39 6

Sample Output

242

Source 2009 Multi-University Training Contest 4 - Host by HDU

題目鏈接：http://acm.hdu.edu.cn/showproblem.php?pid=2845

題目大意：在一個矩陣中選擇一些數，要求和最大，如果選擇(x,y)位置的數，則(x, y+1)，(x,y-1)位置不可選，第x+1和第x-1行都不可選

題目分析：題目給了m*n的范圍，就是不讓你開二維開開心心切掉，不過不影響，一維照樣做，先對於每一行dp一下，求出當前行能取得的最大值
tmp[j] = max(tmp[j - 1]，a[i + j - 1] + tmp[j - 2])第一個表示不選第i行第j列得數字，第二個表示選，取最大，則最後tmp[m]為當前行最大的
然後因為相鄰兩行不能同時取，我再對行做一次dp
dp[i] = max(dp[i - 1], dp[i - 2] + row[i])，第一個表示不選第i行，第二個表示選第i行，取最大，則最後dp[cnt - 1]即為答案

#include 
#include 
#include 
using namespace std;
int const MAX = 2 * 1e5 + 5;
int row[MAX], a[MAX], dp[MAX], tmp[MAX];

int main()
{
    int n, m;
    while(scanf(%d %d, &n, &m) != EOF)
    {
        memset(tmp, 0, sizeof(tmp));
        memset(dp, 0, sizeof(dp));
        for(int i = 1; i <= m * n; i++)
            scanf(%d, &a[i]);
        int cnt = 1;
        for(int i = 1; i <= m * n; i += m)
        {
            for(int j = 2; j <= m; j++)
            {
                tmp[1] = a[i];
                tmp[j] = max(tmp[j - 1], a[i + j - 1] + tmp[j - 2]);
            }
            row[cnt ++] = tmp[m];
        }
        dp[1] = row[1];
        for(int i = 2; i < cnt; i++)
            dp[i] = max(dp[i - 1], dp[i - 2] + row[i]);
        printf(%d
, dp[cnt - 1]);
    }
}